Нахождение объема выборочной совокупности.

Формула

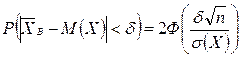
связывает δ (точность оценки), доверительную вероятность 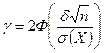и объем выборки. Зная две из этих величин, можно найти третью. Важной является задача определения объема выборочной совокупности n при заданной доверительной вероятности γ и заданном доверительном интервале, определенном точностью δ. Как найти такой минимальный объем выборки n, чтобы оцениваемый параметр накрывался доверительным интервалом с заданной вероятностью γ? Обозначим 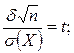тогда

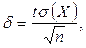
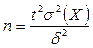
Здесь σ(Х)– среднее квадратическое отклонение, t – значение независимой переменной в функции Лапласа, для которой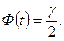

Пример.Высота стебля кукурузы X – случайная величина, имеющая нормальное распределение. Сколько необходимо отобрать растений, чтобы 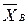отличалось от М(Х)меньше чем на 2 см, если известно, что по результатам предыдущих измерений σ(Х) = 6см. Результат найти с надежностью γ – 0,95.

Решение. Имеем γ = 0,95, Ф(t) = 0,475, t = 1,96

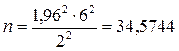
Таким образом, n ≥ 35

1.8. ОЦЕНКА СУЩЕСТВЕННОСТИ РАЗЛИЧИЙ
ВЫБОРОЧНЫХ СРЕДНИХ

Пусть с целью исследования влияния двух факторов на урожай проводились полевые опыты из двух серий по п делянок. Получены следующие результаты: средний урожа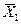й и (ц/га) и исправленные средние квадратические отклонения s₁ и s₂. Как установить, является ли расхождение 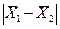случайным, или оно обусловлено влиянием изучаемых факторов? В первом случае расхождение 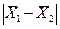называется несущественным, а во втором различие существенно. Следует иметь в виду, что ответ не может быть строго определенным, он либо будет верен с некоторой вероятностью g, либо ошибочен с вероятностью р = 1 — g, называемой уровнем значимости.

Составим случайную величину

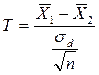(1)

где 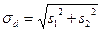, п – объем выборки (число делянок в серии). Доказано, что случайная величина Т имеет t – распределение Стьюдента, для которого составлены таблицы.

Случайная величина Т зависит от числа степеней свободы v = 2(п – 1) и уровня значимости р. По заданному р и числу степеней v находится t теоретическое.

По формуле (13.8.1) находят t практическое:

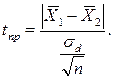
Если t_пр < t_теор, то с вероятностью ошибки, равной р, считают, что расхождение между средними незначимо, и влияние факторов на урожайность существенным признать нельзя. Если, t_пр ≥ t_теор, то расхождение между средними выборочными существенно, оно объясняется влиянием изучаемых факторов.

Если объем выборочных совокупностей неодинаков, то используют более сложные формулы, которые можно найти в подробных курсах (например, [8]).

Пример. В результате полевых испытаний выращен урожай двух сортов картофеля: «Приекульский ранний» и «Дружба». Отобрано по 25 клубней каждого сорта. Результаты взвешивания таковы: выборочное среднее значение и исправленное среднее квадратическое отклонение массы одного клубня сорта «Приекульский» равны 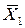= 65 г, s₁ = 15 г, для сорта «Дружба» =90 г, s₂ = 20г.

На уровне, значимости р = 0,05 проверить существенность различий выборочных средних.

Решение. Находим

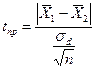
Число степеней свободы р = 2(25 – 1) = 48. Далее получаем t_теор = 2,01, т.е. t_пр > 1_теор. Расхождение существенно. Принимается утверждение, что обе выборки сделаны из разных генеральных совокупностей, т. е. влияние сорта значимо.

ВЫВОДЫ

Математическая статистика занимается изучением и разработкой методов сбора, регистрации и обработки статистического материала.

Основным понятием математической статистики является статистическое распределение. Статистическим распределением выборки называется соответствие между количественными признаками и их частотами или относительными частотами. По нему составляется эмпирическая функция распределения, являющаяся оценкой функции распределения признака в генеральной совокупности. Для параметров распределения признака в генеральной совокупности находят точечные и интервальные оценки. Оценка называется точечной, если она характеризуется одним числом. Точечными оценками параметров распределения, в частности, служат выборочная средняя, выборочная дисперсия, исправленная выборочная дисперсия. При малом объеме выборки точечная оценка может намного отличаться от оцениваемого параметра.

Оценка, определяемая двумя числами, – концами интервалов, называется интервальной. Интервал (θ* – δ, θ + δ), который накрывает оцениваемый параметр с вероятностью γ называется доверительным. Вероятность γ называется доверительной. Между доверительным интервалом, доверительной вероятностью и объемом выборки существует тесная связь. Для случая нормально распределенного признака в генеральной совокупности эта связь определяется формулой

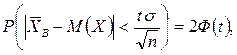
где 2Ф(t) = γ, t = Ф^–1 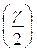, Ф^–1 (Х)– функция, обратная функции Лапласа.

Важное практическое значение этой формулы состоит в том, что по ней можно заранее установить минимальный объем выборочной совокупности при известных других величинах так, чтобы с заданной вероятностью отклонение выборочной средней от математического ожидания не превышало заранее назначенной величины.

* Утверждение, что Х_в имеет нормальное распределение, принимается без доказательства.