Координатное и векторное описание положения частицы, связь между ними.

Физические модели.

Модель - совокупность основных черт явления.

1. Инерциальная система отсчета. (И.С.О.)

2. Материальная точка.

3. Модель абсолютно твердого тела.

И.С.О. - это такая система, относительно которой, материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно.

Система отсчета – тело отсчета (или система неподвижных относительно друг друга тел) условно принятое за неподвижное.

Материальная точка – тело, размером которого в данной задаче можно пренебречь.

Абсолютно твердое тело – система материальных точек, изменением расстояния между которыми в данной задаче можно пренебречь.

Координатное и векторное описание положения частицы, связь между ними.

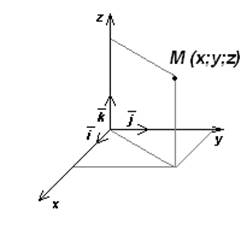[1]

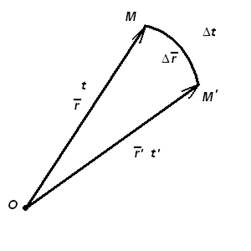
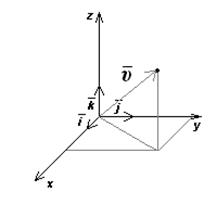
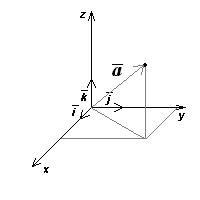
Радиус-вектор – =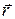

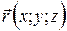
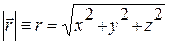
Меняются со временем:

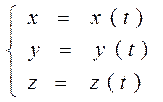
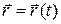
Кинематическое уравнение движения

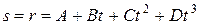
Задавая зависимость 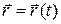и получив геометрическое место точек концов 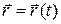, мы определим траекторию движения материальной точки.

4. Скорость и ускорение материальной точки

Прямолинейный отрезок, соединяющий начало и конец траектории, называется перемещением материальной точки.

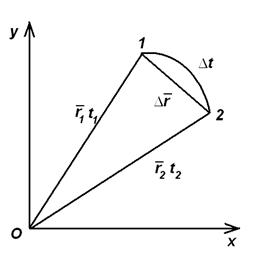
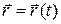
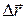– перемещение

( = )

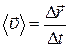
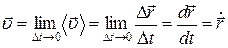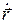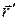Средняя скорость сонаправлена с вектором перемещения. Мгновенная скорость направлена по касательной к дуге окружности.

;

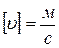
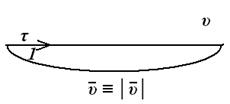
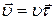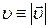
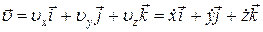
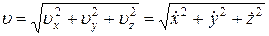
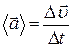
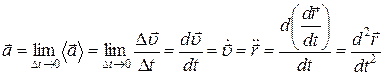
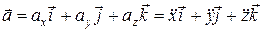
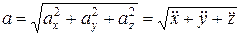
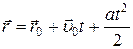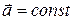
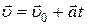, при

, при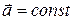

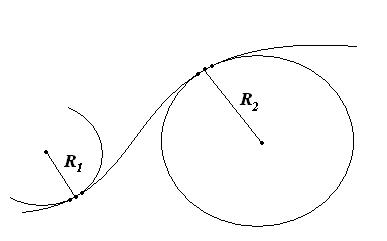
5. Нормальное и тангенциальное ускорение. Радиус кривизны траектории

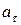– (тангенциальное) отвечает за изменение скорости по модулю

– (нормальное) отвечает за изменение скорости по направлению

;

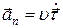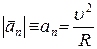
R – радиус кривизны траектории – радиус окружности, проведённой через три бесконечно близкие точки траектории.

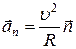
Вид движения в зависимости от 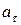и :

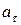
№			Вид движения
			равномерное, прямолинейное
	const		равнопеременное, прямолинейное
	f(t)		с переменным ускорением, прямолинейное
		const	равномерное, по окружности
	const	const	равнопеременное, по окружности
	const	f(t)	равнопеременное, криволинейное
	f(t)	f(t)	с переменным ускорением, криволинейное
		f(t)	равномерное, криволинейное
	f(t)	const	с переменным ускорением, по окружности