Закон сохранения импульса. Рассмотрим систему, состоящую из N частиц (материальных точек)
Рассмотрим систему, состоящую из N частиц (материальных точек). Обозначим через Fik силу, с которой k-я частица действует на i-ю (первый индекс указывает номер частицы, на которую действует сила, второй индекс - номер частицы, воздействием которой обусловлена эта сила). Символом Fi обозначим результирующую всех внешних сил, действующих на i-ю частицу. Напишем уравнения движения всех N частиц:
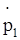 =F12 + F13 +. + F1k +. + F1N + F1=
=F12 + F13 +. + F1k +. + F1N + F1= 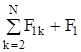 ,
,
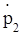 =F21 + F23 +. + F2k +. + F2N + F2=
=F21 + F23 +. + F2k +. + F2N + F2= 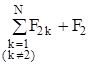 ,
,
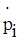 =Fi1 + Fi2 +. + Fik +. + FiN + Fi =
=Fi1 + Fi2 +. + Fik +. + FiN + Fi = 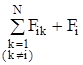 ,
,
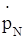 =FN1 + FN2 +. + FNK +. +FN,N-1 + FN =
=FN1 + FN2 +. + FNK +. +FN,N-1 + FN = 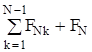
(pi - импульс i-й частицы).
Сложим вместе эти уравнения. Слева получиться производная по времени от суммарного импульса системы:
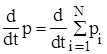 .
. 
Справа отличной от нуля будет только сумма внешних сил Fi. Действительно, сумму внутренних сил можно представить в виде
(F12+F21) + (F13 + F31) +. + (Fik + Fki) +. + (FN-1,N + FN,N-1).
Согласно третьему закону Ньютона каждая из скобок равно нулю. Следовательно, сумма внутренних сил, действующих на тела системы, всегда равна нулю:
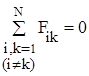 .
.
С учетом этого получим, что
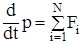 . (1)
. (1)
Таким образом, производная по времени от суммарного импульса системы равнасумме внешних сил, действующих на тела системы.
Если система замкнута, внешние силы отсутствуют и правая часть уравнения (1) равна нулю. Соответственно dp/dt=0 и, следовательно, p=const.
Итак, мы пришли к выводу, что суммарный импульс замкнутой системыматериальных точек остается постоянным. Это утверждение составляет содержание закона сохранения импульса.
В основе закона сохранения импульса лежит однородность пространства, т.е. одинаковость свойств пространства во всех точках. Параллельный перенос замкнутой системы из одного места в другое без изменения взаимного расположения и скоростей частиц не изменяет механических свойств системы. Поведение системы на новом месте будет таким же, каким оно было бы на прежнем месте.
Заметим, что согласно формуле (1) импульс остается постоянным и у незамкнутой системы в том случае, если сумма всех внешних сил равна нулю.
Спроектировав все векторы, фигурирующие в уравнении (1), на некоторое направлениеx, получим
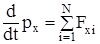 (2)
(2)
( 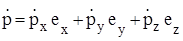 ; отсюда следует, что проекция на ось x вектораp равна dpx/dt). Согласно (2) для того, чтобы сохранялась проекция суммарного импульса на некоторое направление, достаточно равенства нулю проекции на это направление суммы внешних сил; сама эта сумма может быть отличной от нуля.
; отсюда следует, что проекция на ось x вектораp равна dpx/dt). Согласно (2) для того, чтобы сохранялась проекция суммарного импульса на некоторое направление, достаточно равенства нулю проекции на это направление суммы внешних сил; сама эта сумма может быть отличной от нуля.
Точка С, положение которой определяется радиус-вектором
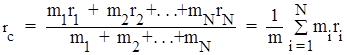
называется центром масс системы материальных точек. Здесь mi - масса i-й частицы, ri - радиус-вектор, задающий положение этой частицы, m - суммарная масса системы. Отметим, что в однородном поле сил тяжести центр масс совпадает с центром тяжести системы.
Спроектировав rc на координатные оси, получим декартовы координаты центра масс:
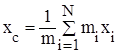 ,
, 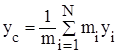 ,
, 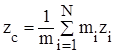 .
. 
Продифференцировав rc по времени, найдем скорость центра масс:
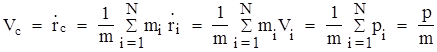 (3)
(3)
Согласно (3) суммарный импульс системы можно представить в виде произведения массы системы на скорость центра масс:
p=mVc
Подставив это выражение в формулу (1), получим уравнение движения центра масс:
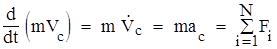

(ас - ускорение центра масс). Таким образом, центр масс движется так, как двигалась бы материальная точка с массой равной массе системы, под действием результирующих всех внешних сил, приложенных к телам системы. Для замкнутой системы ас=0. Это означает, что центр масс замкнутой системы движется прямолинейно и равномерно, либо покоится.
Система отсчета, относительно которой центр масс покоится, называется системой центра масс (сокращенно ц-системой). Эта система иннерциальна. Система отсчета, связанная с измерительными приборами, называется лабораторнойсистемой (сокращенно л-системой).
Дата добавления: 2015-09-18; просмотров: 675;
