Дисперсия света.

Опыт показывает, что скорость света 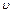в среде зависит от длины волны света 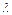( 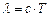- расстояние, которое световая волна проходит за один период. Период 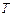- время одного полного колебания). В видимом диапазоне длин волн, скорость минимальна для фиолетовых лучей ( 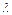_ф ≈ 400 нм) и максимальна для красных лучей ( 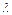_кр ≈ 760 нм).

Дисперсия света – это явление, обусловленное зависимостью показателя преломления n от частоты 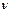(длины волны 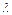) света или зависимостью фазовой скорости световых волн от их частоты (смотри приложение). Все среды, за исключением абсолютного вакуума, обладают дисперсией.

Абсолютным показателем преломления среды n называется физическая величина, определяемая отношением скорости света в вакууме с (с ≈ 3∙10⁸ м/с) к фазовой скорости света 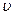в среде

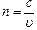
Таким образом, скорость света в среде связана с показателем преломления вещества соотношением:

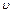=c/n.

Согласно электромагнитной теории Максвелла абсолютный показатель преломления среды

,

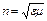где 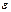-диэлектрическая проницаемость среды, 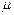-магнитная проницаемость. В оптической области спектра для всех прозрачных диэлектриков 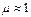, поэтому имеем

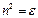или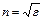

Дисперсия света может быть охарактеризована функцие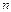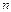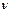й = ( ) или 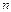= 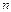( 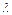), поскольку длина волны и частота связаны соотношением .

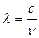Дисперсией вещества называется величина 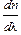, определяющая степень растянутости спектра вблизи данной длины волны 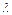. Дисперсия называется нормальной, если с ростом длины волны показатель преломления уменьшается, т.е. 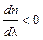и аномальной, если 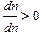(рис.5-1 и рис.5-3). Для прозрачных веществ характерно монотонное возрастание показателя преломления с уменьшением длины волны (рис. 5-1).

Рис. 5-1. Зависимость показателя преломления среды 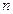от длины световой волны 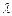и ее частоты 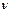в случае нормальной дисперсии.

В своем, ставшим классическим, опыте по разложению белого света Ньютон столкнулся с дисперсией света, еще не подозревая об электромагнитной природе световых волн. Опыт Ньютона состоял в том, что узкий пучок солнечного света он направил на боковую грань трехгранной призмы, а при выходе пучка из противоположной боковой грани наблюдались разноцветные лучи в следующей последовательности – красный(К), оранжевый(О), желтый(Ж), зеленый(З), голубой(Г), синий(С), фиолетовый (Ф) (рис.5-2). Полученную им цветную полоску Ньютон назвал спектром.

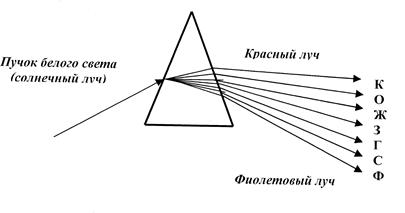
Рис.5-2. Разложение белого света в спектр 3-хгранной призмой.

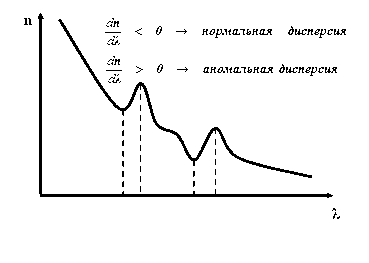
Рис. 5-3. Зависимость показателя преломления среды 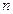от длины световой волны 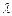в случае нормальной и аномальной дисперсии.

Основы теории дисперсии света могут быть получены, если рассматривать взаимодействие световых волн с электронами атомов. Теоретическому рассмотрению проще всего поддается дисперсия в газах, т.к. в этом случае в первом приближении можно не учитывать сложное взаимодействие атомов и молекул среды. Согласно современным научным представлениям, движение электронов в атоме подчиняется законам квантовой механики, а не классической физики, тем не менее, как показал Лоренц, для качественного понимания многих оптических явлений достаточно ограничится гипотезой о существовании внутри атомов квазиупруго связанных электронов. Электроны, входящие в состав атомов, можно разделить на периферийные, так называемые, оптические, и электроны внутренних оболочек. На излучение ипоглощение света в оптическом диапазоне влияние оказывают лишь оптические электроны. Для простоты предположим сначала, что в атоме есть всего один оптический электрон. В классической теории оптический электрон можно рассматривать как затухающий гармонический осциллятор, вынужденные колебания которого происходят под действием переменного поля электромагнитной световой волны и описываются дифференциальным уравнением, представляющим собой уравнение движения электрона:

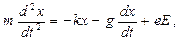
где m – масса электрона, e – его заряд, k – константа, аналогичная коэффициенту упругости, x – смещение электрона, kx - квазиупругая возвращающая сила, стремящаяся вернуть электрон в положение равновесия, 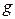- константа, аналогичная коэффициенту сопротивления при рассмотрении затухающих колебаний, 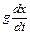- сила, аналогичная силе трения и формально введенная для учета поглощения света, 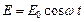– напряженность действующего на электрон электрического поля световой волны, имеющей циклическую частоту 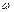и амплитуду E₀

Уравнения движения электрона можно также переписать в виде:

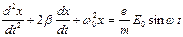
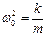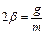
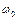где введены следующие обозначения: и - собственная частота осциллятора, 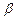- коэффициент затухания.

В предположении, что сила сопротивления незначительна (коэффициент сопротивления 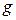=0, что приводит и к = 0), уравнение движения электрона можно упростить и записать его в виде:

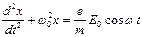
Теория дифференциальных уравнений позволяет найти решение этого уравнения в виде: 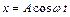, где амплитуда вынужденных колебаний электрона:

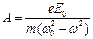
Таким образом, амплитуда вынужденных колебаний оптического электрона зависит от соотношения частот 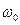и .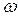

Если рассматривать молекулы или атомы диэлектрика как системы, в состав которых входят электроны, находящиеся в молекулах в состоянии равновесия, то под влиянием электрического поля световой волны эти заряды смещаются из положения равновесия на расстояние x , превращая таким образом молекулу в электрическую систему с электрическим моментом 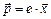(дипольный момент). Поляризованность, определяется как дипольный момент единицы объема диэлектрика 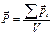. При концентрации атомов в диэлектрике равной 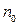численное значение поляризованности единицы объема можно рассчитать по формуле: .

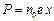Для изотропных диэлектриков (исключая сегнетоэлектрики) поляризованность 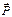линейно зависит от напряженности электрического поля 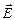: 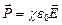. По определению, диэлектрическая восприимчивость среды 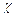и диэлектрическая проницаемость 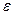связаны соотношением: 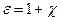и тогда можно записать, что

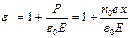
Поскольку 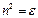, то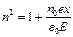

Теперь, чтобы получить выражение для определения показателя преломления, необходимо подставить вместо x его значение, ранее полученное из решения соответствующего дифференциального уравнения. Окончательно получим выражение для зависимости показателя преломления от частоты световой волны в виде

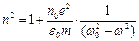или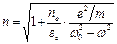

Рис.5-4 дает графическое представление этой зависимости.

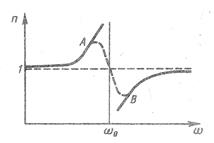
Рис. 5-4. Зависимость показателя преломления n от частоты вблизи одной из резонансных частот .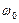

Если в веществе имеются электроны, совершающие вынужденные колебания с различными собственными частотами ω_{оi ,} то

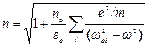
где n_o – концентрация атомов, ω_оi – собственные частоты колебаний электронов, m – масса электрона, ε_о – электрическая постоянная.

Рассмотрение всего ансамбля оптических электронов приводит к заключению, что электроны в атомах обладают определенным набором собственных частот колебаний ω_оi . Графическая зависимость такого рассмотрения дана на рис. 5-5.

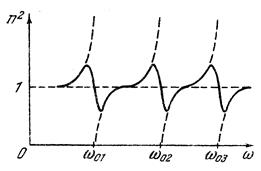
Рис.5-5. Зависимость показателя преломления от частоты 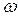при наличии нескольких резонансных частот .

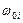Все силы, действующие внутри атомов и молекул, имеют электрическую природу. Однако объяснить этими силами существование и структуру атомов и молекул классическая физика не в состоянии. Это было сделано в рамкахквантовой механики и привело к поразительному результату, что в отношении дисперсии и поглощения света атомы и молекулы ведут себя так, как если бы среда представляла собой набор осцилляторов с различными собственными частотами и коэффициентами затухания, подчиняющимися классическим уравнениям Ньютона, т.е., законам классической физики. Однако нужно не забывать, что собственные частоты и коэффициенты затухания не могут быть вычислены на основе классической модели. Их нужно рассматривать как формально введенные постоянные, а их истинный физический смысл может быть раскрыт только в рамках квантовой теории. Классическая теория представляет лишь модель, которая, тем не менее, приводит к правильным окончательным результатам.

Итак, теория предполагает, что электроны, обладающие в атомах и молекулах набором собственных частот колебаний ω_оi , под действием падающей световой волны совершают вынужденные колебания с частотой ω, совпадающей с частотой падающей световой волны.

Первичная электромагнитная волна, распространяясь в веществе, вызывает вынужденные колебания электронов, и они становятся источниками вторичных волн. Вторичные волны, складываясь с первичной, образуют результирующую волну с амплитудой и фазой, отличными от амплитуды и фазы первичных волн. В результате волна проходит через вещество с фазовой скоростью, отличной от скорости, с которой она распространялась бы в вакууме.

Все изложенное относится к излучению изолированного атома. В случае среды, состоящей из близко расположенных атомов, надо принять во внимание, что атом не только теряет энергию на излучение, но и получает энергию, излучаемую другими атомами. Если среда оптически однородна, то оба эти процесса в точности компенсировали бы друг друга. В отсутствие других причин затухания колебания атома были бы незатухающими. Таким образом, плоская бегущая световая волна распространялась бы в идеализированной среде без ослабления.