Частные математические модели динамических систем
В зависимости от конкретных свойств множеств X, Z, Y и отображений s и h можно получить математические модели различных классов систем. Так, если множество Т непрерывно, то получаем класс непрерывных систем. Если множество Т дискретно, то получаем класс дискретных систем. Если в классе дискретных систем потребовать, чтобы множества X, Z, Y имели конечное число элементов, то получим класс конечных автоматов, который описывается достаточно просто: для него достаточно использования методов алгебры и логики. Класс конечных автоматов охватывает большое количество реальных систем: дискретные (цифровые) измерительные, управляющие и вычислительные устройства, в том числе и компьютеры. Ввиду широкого распространения конечных автоматов более подробное описание этих моделей приведено в п. 2.2.2.
Если X, Y, Z – линейные пространства, а s и h – линейные операторы, то получается класс линейных систем. Напомним, что основное свойство линейных систем состоит в выполнении принципа суперпозицииреакция системы (выход) на сумму входных воздействий равна сумме реакций на каждый их них в отдельности. Если к линейной модели предъявить дополнительные требования топологической структуры пространств X, Y, Z (это означает, что на множествах X, Y, Z должна существовать сходимость последовательностей и быть определена метрика), а также непрерывности операторов s и h, то получим класс гладких систем. Этот класс имеет большое значение, поскольку оказалось, что для гладких систем переходное отображение s является общим решением дифференциального уравнения: 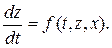
Для дискретных систем s является решением конечно-разностного уравнения:

где x(×) – траектория для моментов времени 
Дата добавления: 2015-09-18; просмотров: 811;
