ПОДОБИЕ ОПТИМАЛЬНЫХ СТРУКТУР И ДВЕ ТЕОРЕМЫ В ТЕОРИИ ИСК

В основе моделирования исследований и общих законов измене­ния свойств в теории ИСК лежит важное научное положение о подобии оптимальных структур. Имеется в виду подобие геометри ческое, физическое и технологическое. Как известно, фундаменталь­ные работы в области теории подобия выполнены Бертраном Н.С., Кирпичевым В.Л., Афанасьевой Т.А., Кирпичевым М.В., Седо­вым Л.И., Гухманом А.А., Вениковым В.А. и др. Были разработаны и убедительно доказаны три теоремы о подобии систем, а также о соответствующем их моделировании.

Геометрическое подобие в этой теории устанавливается при усло­вии равенства сходственных углов и пропорциональности сходствен­ных длин у геометрических фигур одинаковой формы. В оптимальных структурах искусственных конгломератов, размещающихся на гипер­болических кривых MN₁ или параболических кривых MN₂ (см. рис. 3.8), в качестве таких геометрических фигур выступают континуаль­ные пленки связующего вещества или матрицы. Вдоль упомянутых ги­перболической или параболической кривых оптимальных структур отношение толщин δ/ δ * этих пленок, умножаемых на соответствую­щие коэффициенты масштабов подобия, остаются пропорциональны­ми величинами. Другой геометрической фигурой практически одинаковой формы вдоль упомянутых кривых оптимальной структу­ры выступают сферические поры. С увеличением заполняющей части в конгломерате диаметр пор возрастает, что фиксируется с помощью коэффициентов масштабов подобия, как это было в случае отношений толщин пленок. Количество пор (пористость в единице объема) вдоль кривой оптимальных структур остается практически одинаковым (2—3%). Наличие этих двух сходственных элементов структуры и их количественных пропорциональностей фиксирует геометрическое подобие оптимальных структур.

Геометрическому подобию оптимальных структур сопутствует их физическое подобие. Физические явления, процессы или системы подобны, если сходственные величины, характеризующие состояние системы (в данном случае — оптимальной структуры) пропорцио­нальны соответствующим величинам другой системы (т. е. другой оптимальной структуры конгломерата).

Для доказательства физического подобия оптимальных структур в теории ИСК используется ее первая теорема. Имеются два произволь­ных ИСК оптимальной структуры — А и Б. В отношении каждого из них действуют закономерности, которые ранее были установлены для материалов с конгломератным типом структуры. Требуется доказать, что конгломерат А физически подобен конгломерату Б. Для доказате­льства возможно использовать каждую из трех теорем, известных в те­ории подобия, или привлечь всех их вместе.

Согласно теореме подобия в формулировке М.В. Кирпичева (из­вестной как первая теорема теории подобия), «подобные явления описываются буквенно-одинаковыми уравнениями, которые услов­но или безусловно инвариантны по отношению к подобным преоб­разованиям входящих в них величин». Известно, что в теории ИСК одинаковыми буквенными уравнениями описываются прочность и вне зависимости от напряжения, которое она выражает, деформативность и, в частности, величина упругих, не пластических (т. е. об­ратимых) деформаций. Соответствующей им величиной выражается и модуль упругости. В буквенные сходственные выражения уравне­ний входят подобные и притом инвариантные физические величины как характеристики оптимальных структур вяжущего вещества (матрицы) и качества заполняющего компонента конгломератов. Так, например, по условию доказываемой теоремы прочность конг­ломерата А равна: 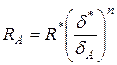, а прочность конгломерата Б равна: 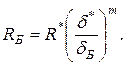Понятно, что обе эти формулы являются апостериорными. Однако, исходя из подобия, возможно априори написать, что прочность еще одного конгломерата, например В, будет равна: 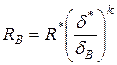и т. д. Таким образом, в полном согласии с теоремой М.В. Кирпичева «подобные явления описываются буквенно одина­ковыми уравнениями» и, следовательно, принятые по условию конг­ломераты А, Б, В оптимальной структуры геометрически и физиче­ски подобны между собой, что и требовалось доказать.

Для доказательства первой теоремы теории ИСК можно воспо­льзоваться и второй теоремой теории подобия, называемой также Пи-теоремой и в свое время доказанной Бэкингемом, Т.А. Афанась­евой и др. В ней при подобии явлений и систем устанавливается связь не только между реальными размерными — именованными — величинами, как по первой теореме М.В. Кирпичева, но и между их безразмерными комбинациями, именуемыми критериями подобия.

В теории ИСК из общей формулы прочности (и других свойств) следует, что 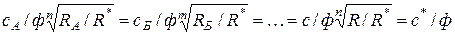, где с*/ф выступает как инвариант подобия, а величина 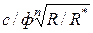— как кри­терий подобия. Все числовые значения являются безразмерными, что полностью удовлетворяет условиям Пи-теоремы, а следовательно, конгломераты А и Б физически (при ранее отмеченном геометриче­ском подобии) подобны между собой, что и требовалось доказать.

Для доказательства первой теоремы ИСК можно воспользо­ваться и третьей теоремой теории подобия, выведенной М.В. Кирпичевым и А.А. Гухманом. Она устанавливает следующие необхо­димые и достаточные условия для подобия явлений и систем: геометрическое подобие, буквенная одинаковость уравнений (т. е. соблюдение первой теоремы теории подобия). Достаточным услови­ем является равенство определяющих критериев подобия (т. е. вто­рая теорема теории подобия) или равенство единице критерия подо­бия, называемого тогда индикатором подобия. Выше показано, что в теории ИСК принят индикатор подобия А, предложенный И.А. Рыбьевым:

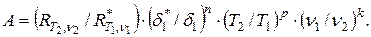(3.16)

При оптимальных структурах А = 1 и, следовательно, согласно тре­тьей теореме теории подобия, конгломераты (в данном случае конг­ломераты А и Б) оптимальных структур подобны между собой, что и требовалось доказать.

Подобие структур сохраняется не только в данный момент, но и в течение времени, т. е. оно носит временной характер. Следует то­лько обеспечить необходимую долговечность ИСК по его структур­ным и, следовательно, экстремальным качественным показателям. Временной характер подобия в теории ИСК указывает на техноло­гическое подобие конгломератов оптимальной, структуры.

Цементные бетоны, асфальтобетоны, пластмассы, строительные растворы, древесностружечные плиты и т. п. применяют в конструк­циях нередко в виде сложных сочетаний в системах, в которых отде­льные конгломераты выступают в качестве подсистем. Однако и в этом случае каждый материал в системе должен иметь по возможно­сти свою оптимальную структуру, поскольку тогда обеспечивается наилучшее качество всей конструкции. Согласно теореме В.А. Веникова, если подобны подсистемы, то оказываются подобными и сами системы. Следовательно, материалы оптимальной структуры не то­лько подобны между собой, но и образуют в целом систему (строи­тельную конструкцию) наилучшего качества, что способствует эф­фективному решению многих инженерных задач.

Кроме первой теоремы о подобии конгломератов оптимальной структуры, в теории ИСК имеется еще и вторая теорема — о право­мерности закона конгруэнции для конгломератов оптимальной структуры, изготовленных не только на общем, но и на основе раз­личных вяжущих веществ. Выше, в 3.2.2, закон конгруэнции сфор­мулирован в его полном объеме, однако его третья часть утвержде­ния осталась недоказанной. Поэтому требуется доказать, что существует обязательное соответствие свойств между конгломерата­ми оптимальной структуры при различных числовых значениях вя­жущих веществ, а также показать масштабный критерий подобия в общем уравнении.

Для доказательства написано уравнение прочности конгломера­та при первом вяжущем веществе:

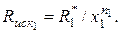
То же — для второго вяжущего вещества: 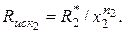Решая эти два

уравнения применительно к первому или второму конгломератам, находится формула (3.3), показанная ранее в 3.2.2. Из той же формулы (3.3) следует, что масштабным показателем подобия является от­ношение расчетных характеристик принятых вяжущих веществ, т. е. безразмерная величина, равная 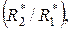или ей обратная. Понятно, что присутствие масштабного показателя не нарушает доказательст­ва первой теоремы о подобии конгломератов оптимальных структур.