Центр мас механічної системи рухається як матеріальна точка, маса якої дорівнює масі механічної системи, під дією зовнішніх сил, прикладених до точок цієї системи.

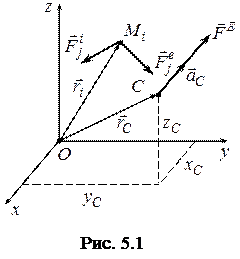Доведення: Нехай механічна система матеріальних точок 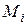рухається під дією зовнішніх ( 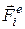) і внутрішніх ( 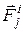) сил відносно обраної системи координат 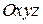(рис. 5.1).

Положення центра мас 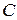системи визначається за формулою:

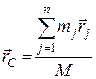, де . (5.1)

Запишемо диференціальні рівняння руху усіх точок механічної системи

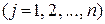. (5.2)

Підсумовуючи рівняння (23.2) за кількістю точок, дістаємо

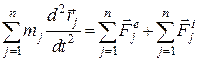. (5.3)

Перетворимо ліву частину рівняння (23.3), з урахуванням формули (5.1):

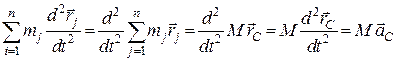. (5.4)

Враховуючи властивості внутрішніх сил механічної системи ( ) та підставляючи значення (5.4) в (5.3), остаточно дістанемо

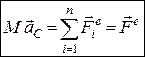. (5.5)

Рівняння (5.5) визначає доведену теорему про рух центра мас.

Проектуючи обидві частини (5.5) на координатні осі, дістаємо диференціальні рівняння руху координат центра мас:

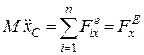; ; . (5.6)

З теореми випливають такі наслідки:

1. Внутрішні сили безпосередньо не впливають на рух центра мас механічної системи. (Вони можуть здійснювати лише непрямий вплив через зовнішні сили).

2 Якщо головний вектор всіх зовнішніх сил, які діють на точки механічної системи, весь час дорівнює нулю, то центр мас механічної системи перебуває в стані спокою або рухається рівномірно і прямолінійно.

Кінематичний стан центра мас при цьому залежить відпочаткової швидкості.

3. Якщо проекція головного вектора всіх зовнішніх сил на будь-яку вісь дорівнює нулю, то проекція центра мас механічної системи на цю вісь залишається нерухомою або рухається рівномірно і прямолінійно.

Другий та третій наслідки називаються законами збереження руху центра мас механічної системи.

5.2. Імпульс сили та його проекції на координатні осі

Спостереження вказують на те, що одна і та сама сила може різним тілам надати однакові кінематичні стани, але при цьому час дії сили на ці тіла повинен бути різним.

Дію сили на матеріальну точку за деякий проміжок часу можна визначити імпульсом сили.

Імпульс сили характеризує передачу матеріальній точці механічного руху за деякий проміжок часу з боку інших тіл, з якими взаємодіє дана матеріальна точка.

Якщо сила, що діє на матеріальну точку, є сталою за модулем і напрямом, то імпульс сили за проміжок часу дорівнює добутку вектора сили на проміжок часу τ і має напрям цієї сили, тобто:

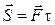, (5.7)

де

.

Якщо сила, що діє на точку, змінюється з плином часу за модулем чи напрямом, то проміжок часу розбивають на елементарні проміжки часу, вважаючи при цьому силу сталою, а потім обчислюють інтегральну суму елементарних імпульсів

; (5.8)

. (5.9)

Проектуючи обидві частини (23.9) на координатні осі маємо:

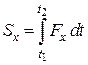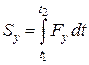; ; . (5.10)