Неравенства Коши и теорема Лиувилля.

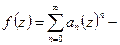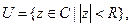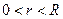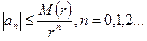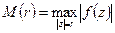Теорема. Если сходится в круге то для любого выполняется неравенство Коши: где (норма функции f).

Доказательство. Напишем формулу Коши для производной в нуле (для коэффициентов ряда): 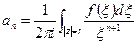. Оценим этот интеграл: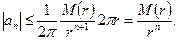

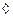
Теорема (Лиувилля). Если 1) f – голоморфна в С 2) f – ограничена в С , то f = const.

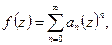
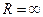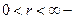Доказательство. Разложим функцию в ряд Тейлора: - радиус сходимости (т.к. ряд сходится во всей плоскости, т.к. функция голоморфна). по неравенству Коши любое. Зафиксируем 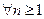и перейдём к пределу при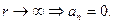

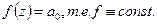
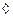
Задача. 1) f – голоморфна в С 2) 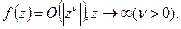Тогда f – многочлен степени не выше 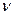(или целая часть 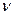, что одно и тоже).

ОСОБЫЕ ТОЧКИ СТЕПЕННОГО РЯДА