Определение. Если конечно, то кривая называется спрямляемой.
Замечание. В терминах действительного анализа спрямляемая кривая – непрерывная функция ограниченной вариации.
Задача. 1) Доказать, что длина кривой не зависит от выбора параметризации.
Пусть 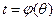 - строго возрастающая и непрерывная функция на
- строго возрастающая и непрерывная функция на 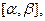 т.ч.
т.ч. 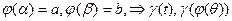 - имеют одну и ту же длину.
- имеют одну и ту же длину.
2) Доказать, что 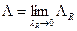 ,
, 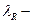 параметр разбиения, т.е.
параметр разбиения, т.е. 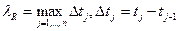 .
.
3) Привести пример не спрямляемой кривой.
Определение. 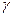 - гладкая кривая, если функция непрерывна, дифференцируема на отрезке [a,b] и
- гладкая кривая, если функция непрерывна, дифференцируема на отрезке [a,b] и 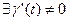 .
.
Задача. Доказать, что длина гладкой кривой вычисляется по формуле: 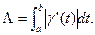
Дата добавления: 2015-09-02; просмотров: 1437;
