Оценка качества количественных прогнозов

Для оценки качества прогноза, разработанного с применением формализованных методов, принято использовать такие характеристики как надёжность, точность, достоверность, ошибки прогноза.

Под надёжностью прогнозных расчётов понимается мера неопределённости поведения объекта прогнозирования во времени.

Достоверность прогноза определяется вероятностью осуществления прогноза для заданного варианта или доверительного интервала.

Точность прогноза характеризует интервальный разброс прогнозных траекторий при фиксированном уровне достоверности.

Ошибки прогноза представляют собой меру отклонения прогнозных оценок от реальных значений состояния прогнозируемого объекта.

Однако, описать такие характеристики как надёжность, точность, достоверность, вычислить ошибки прогноза априори не представляется возможным, поскольку прогнозные результаты не с чем сравнивать. Поэтому и на сегодняшний день перед разработчиками прогнозов встаёт проблема: «Как оценить качество прогноза ещё до его реализации?». Определённые шаги в сторону улучшения качества прогноза можно сделать, изучив факторы, влияющие на показатели качества прогноза (рис. 2.2).

	Качество исходной информации		Модель прогноза		Метод прогнозирования

Рис. 2.2. Факторы, влияющие на качество прогноза

Качество исходной информации, в свою очередь, определяется:

- точностью экономических измерений;

- качеством выборки;

- отсутствием ошибок согласования (данные ошибки возникают в тех случаях, когда исходная информация для проведения прогнозных расчётов подготавливается различными специалистами, использующими разные методологические подходы).

Наибольшие погрешности (стратегические ошибки прогнозирования) возникают в результате неудачного выбора метода прогнозирования. Например, на основании прогнозов социально-экономического развития СССР, проводимых в 1960-е годы, Генеральный секретарь Коммунистической партии Н.С.Хрущёв заверил, что к 1980 году «СССР догонит и перегонит Америку». Стратегическая ошибка прогнозирования была обусловлена тем, что для долгосрочного прогнозирования применялись методы экстраполяции которые, как мы уже знаем, целесообразно использовать для краткосрочного прогнозирования.

Погрешности, связанные с выбором модели прогноза, возникают в результате упрощения, несовершенства теоретических построений или неадекватности моделей прогнозируемым социально-экономическим процессам. Иногда для прогнозирования процессов, протекающих в нашей стране, используются модели разработанные зарубежными специалистами и хорошо себя зарекомендовавшие для прогнозирования аналогичных процессов в других странах. Однако следует помнить о том, что данные модели могут быть неадекватны по отношению к социально-экономическим процессам, происходящим в нашей стране, и их использование может привести к серьезным ошибкам и просчетам.

Результат прогноза, разработанного формализованным методом, чаще всего выражается количественным показателем, которому может быть дана точечная ( 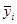) и (или) интервальная оценка ( ).

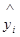Точечная оценка( 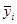) — это единичная оценка прогнозного параметра. Точечные значения экономических величин лишены содержания, так как имеют нулевую вероятность. Для устранения этого недостатка прогноз должен быть дан в виде интервала значений.

Интервальная оценка( 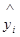) — это числовой интервал (доверительный интервал), в котором, вероятно, находится прогнозный параметр.

Точностьпрогноза тем выше, чем меньше величина ошибки, которая представляет собой разность между прогнозируемыми и фактическими значениями исследуемой величины. Понятие точности прогноза и методы ее оценки отличаются от точности исходных данных. Точность исходных данных может быть однозначно оценена на этапе сбора информации как степень приближения результатов измерений к истинному значению измеряемой величины. На практике часто количественную оценку точности заменяют указанием ошибки измерения (погрешности), которая определяется как разница между оцениваемым результатом и результатом, полученным более точным методом. В прогнозных значениях (до наступления прогнозируемого события) точность обычно также выражается как погрешность, но с помощью вероятностных пределов отклонения фактической величины от прогнозируемого значения, которые принято называть доверительным интервалом.

Заметим, что прогнозируемые значения должны реализоваться в соответствующее время с указанной вероятностью и лежать внутри некоторой доверительной области, ширина которой зависит от заданной вероятности.

Математическая вероятность( 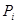) случайной величины равна отношению числа событий, благоприятствующих ее появлению (т.е. свершению прогноза) к общему числу событий (благоприятных и неблагоприятных). Численное значение вероятности прогноза лежит в пределах от 0 до 1.

Очевидно, что точность прогноза максимальна при построении точечного прогноза. Но построить его с высокой степенью вероятности часто не представляется возможным.

В то же время границы доверительного интервала можно задать такими широкими, что прогнозируемое значение попадет туда с любой вероятностью, включая Р = 0 и Р = 1. Такой прогноз называется абсолютно достоверным. Однако границы доверительного интервала будут столь широкими, что полученный прогноз не будет иметь практической ценности для принятия управленческих решений. На практике достаточно иметь вероятность прогноза 0,7-0,95.

Под достоверностьюпрогноза понимается вероятность осуществления прогноза в заданном доверительном интервале .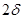

Условная графическая интерпретация доверительного интервала показателя у при заданной вероятности Р представлена на рис. 2.3.

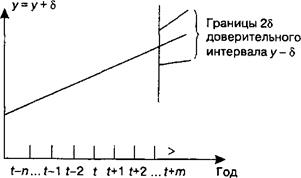
Рис. 2.3. Графическая интерпретация границ доверительного интервала

Существуют неформальный и формальный способы определения доверительного интервала. Неформально доверительный интервал может быть определен экспертами с учетом степени изменчивости фактических значений показателей вокруг расчетных (теоретических) значений в прошлом и возможности деформации в будущем. При этом экспертам может быть предложено оценить суммарную величину ошибки или степень влияния различных составляющих на точность прогноза. Суммарная ошибка решения прогнозной задачи определяется по формуле

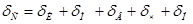, (2.10)

где 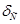— суммарная ошибка;

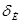— ошибки информации, обусловленные неадекватностью описания объекта, погрешностями получения и обработки информации;

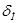— ошибки метода прогнозирования, вызванные невозможностью идеального выбора метола для данного объекта, а также обязательной схематичностью метода;

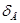— ошибки вычислительных процедур;

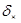— ошибки, допущенные человеком и обусловленные субъективными факторами (низкая квалификация, восторженность, пессимизм);

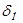— нерегулярная составляющая ошибки, обусловленная возможностью появления непредсказуемых изменений в объекте.

Формально границы доверительного интервала можно определить на основе оценки изменчивости уровней ряда. Чем выше эта изменчивость, тем менее точной может быть расчетная величина и тем шире должен быть доверительный интервал при одной и той же вероятности прогноза.

На практике, получая прогнозный результат в виде точечного значения 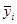, необходимо указать и возможную величину ошибки 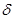, т.е. перейти к интервальному прогнозу по формуле

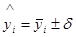, (2.11)

где 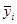— точечное значение прогнозной характеристики;

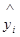— интервальное значение прогнозной характеристики;

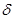— вероятная ошибка прогноза.

Для определения границ доверительного интервала используется выражение

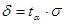, (2.12)

где 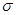— среднеквадратическое отклонение; 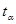— критерий Стьюдента.

Величина среднеквадратического отклонения рассчитывается по формуле

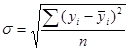, (2.13)

где 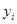— фактическое значение исследуемой характеристики на участке ретроспекции;

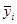— расчетное значение исследуемой характеристики на участке ретроспекции;

п — число наблюдений (размер выборки).

Среднеквадратическое отклонение характеризует, насколько точно теоретическая кривая описывает поведение исследуемой характеристики в прошлом. Величина 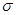определяет минимальную ошибку прогноза. Она зависит, с одной стороны, от корректности модели, с другой — от стабильности исследуемой характеристики в прошлом.

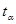— критерий Стьюдента, значение которого зависит от размера выборочной совокупности и заданной вероятности прогноза, использование этого коэффициента определяется ограниченностью выборки (табличные значения критерия Стьюдента приведены в приложении. Критерий Стьюдента позволяет учесть то обстоятельство, что чем выше заданная вероятность прогноза и чем меньше размер выборки, тем шире должны быть границы доверительного интервала.

После наступления прогнозируемого события ошибка прогноза определяется как разность между фактическим и прогнозным значением показателя. Существует несколько способов количественной оценки ошибки прогноза, например, ошибка прогноза или погрешность для каждого момента времени, в котором рассматривается прогноз:

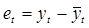, (2.14)

где 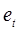— ошибка прогноза в момент времени t,

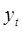— фактическое значение в момент времени t,

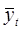— прогнозное значение в момент времени t.

Для обобщенной оценки метода прогнозирования на практике вместе с показателем среднеквадратического отклонения могут быть использованы и другие способы оценки средней ошибки прогноза (погрешности):

· среднее абсолютное отклонение (mean absolute derivation, MAD). Использование этого показателя имеет смысл, когда исследователю необходимо оценить ошибку в тех же единицах, что и исходный ряд:

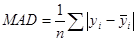; (2.15)

· средняя процентная ошибка (mean percentage error, МРЕ) позволяет оценить возможное смещение прогноза, когда полученный прогноз окажется завышенным или заниженным. При несмещенном прогнозе имеем величину ошибки, близкую к нулю, при завышенном — большое положительное процентное значение, при заниженном — большое отрицательное:

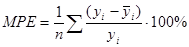; (2.16)

· средняя абсолютная ошибка в процентах (mean absolute percentage error, MAPE):

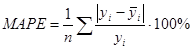. (2.17)

Приведенные выше способы оценки качества прогноза позволяют осуществить сравнение результатов, полученных различными методами прогнозирования, и выбрать наиболее приемлемый метод для решения прогнозной задачи.