Преобразование Фурье
Прямое преобразование Фурье 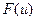 непрерывной функции одной переменной
непрерывной функции одной переменной 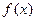 определяется равенством:
определяется равенством:
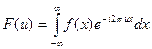 .
.
По заданному преобразованию Фурье 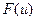 можно получить исходную функцию
можно получить исходную функцию 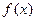 при помощи обратного преобразования Фурье:
при помощи обратного преобразования Фурье:
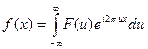 .
.
Для функции двух переменных 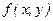 прямое преобразование Фурье
прямое преобразование Фурье 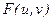 :
:
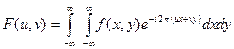 ,
,
Обратное:
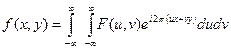 .
.
Преобразование Фурье дискретной функции одной переменной 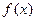 ,
, 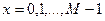 , - дискретное преобразование Фурье (ДПФ) - определяется равенством:
, - дискретное преобразование Фурье (ДПФ) - определяется равенством:
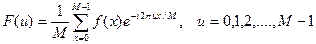 .
.
Исходная функция восстанавливается при помощи обратного ДПФ:
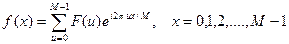 .
.
Понятие частотной области прямо следует из формулы Эйлера: 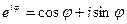 :
:
тогда
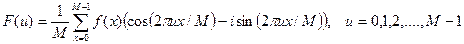 .
.
Таким образом, каждый элемент преобразования Фурье 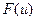 состоит из суммы по всем значениям функции
состоит из суммы по всем значениям функции 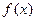 . Значения функции
. Значения функции 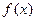 , в свою очередь, умножаются на синусы и косинусы разных частот. Область значений переменной
, в свою очередь, умножаются на синусы и косинусы разных частот. Область значений переменной 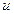 , на которой принимает свои значения функция
, на которой принимает свои значения функция 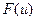 , называется частотной областью, поскольку значения переменной
, называется частотной областью, поскольку значения переменной 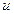 определяют частоты слагаемых, составляющих преобразование. (Значения переменной
определяют частоты слагаемых, составляющих преобразование. (Значения переменной 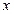 также влияют на частоты, но поскольку по этой переменной производится суммирование, это влияние одинаково для всех значений переменной
также влияют на частоты, но поскольку по этой переменной производится суммирование, это влияние одинаково для всех значений переменной 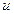 ). Каждый из
). Каждый из 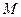 элементов функции
элементов функции 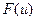 называется частотной компонентой преобразования.
называется частотной компонентой преобразования.
Модулем или спектром Фурье-преобразования называется величина:
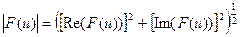 ,
,
Фазой или фазовым спектром:
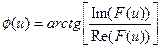 ,
,
Энергетическим спектром называется:
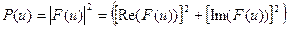 .
.
Дискретное прямое и обратное преобразование Фурье допускает обобщение на двумерный случай. Прямое ДПФ функции 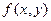 (ЦИ) размерами
(ЦИ) размерами 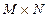 :
:
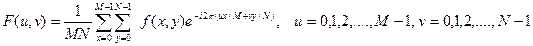 .
.
Обратное ДПФ:
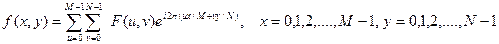 .
.
Переменные 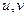 называются частотными переменными, переменные
называются частотными переменными, переменные 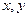 - пространственными переменными или переменными изображения.
- пространственными переменными или переменными изображения.
Фурье-спектр, фаза, энергетический спектр определяются аналогично одномерному случаю:
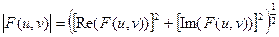 ,
,
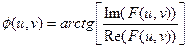 ,
,
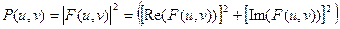 .
.
Значение
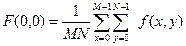
определяет среднее значение функции 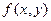 .
.
Дата добавления: 2015-09-18; просмотров: 1756;
