Цифровое изображение

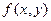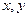Изображение можно определить как функцию , где - координаты на плоскости, значение 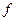которой в любой точке, задаваемой парой координат 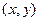, называется интенсивностью или уровнем серого, или градацией серого, или яркостью в этой точке. Если величины 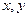, 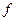принимают конечное число дискретных значений, то говорят о цифровом изображении (ЦИ). Цифровой обработкой изображений называется обработка ЦИ с помощью компьютера. ЦИ состоит из конечного числа элементов, каждый из которых расположен в конкретном месте и принимает определенное значение. Эти элементы называются элементами изображения или пикселями.

Чтобы получить ЦИ, необходимо преобразовать непрерывно поступающий сигнал в цифровую форму. Эта операция включает в себя 2 процесса: дискретизацию и квантование.

Главный принцип, лежащий в основе дискретизации и квантования, проиллюстрирован на рис.1.3. Здесь приведено исходное изображение 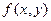, которое мы хотим преобразовать в цифровую форму. Изображение непрерывно по координатам 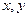, а также по амплитуде 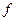. Чтобы преобразовать эту функцию в цифровую форму, необходимо представить ее отсчетами по обеим координатам и по амплитуде. Представление координат в виде конечного множества отсчетов называется дискретизацией, а представление амплитуды значениями из конечного множества – квантованием.

В результате операций дискретизации и квантования возникает матрица действительных чисел. Предположим, что в результате дискретизации изображения 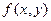получена матрица из М строк и N столбцов. Координаты 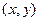становятся теперь дискретными значениями. Для удобства будем использовать для этих координат целочисленные значения (рис.1.4). Надо помнить, что обозначение, например, (0,1) используется лишь для указания на второй отсчет в первой строке, и не означает, что это фактические значения физических координат точек дискретизации.

Тогда полное ЦИ мы можем компактно записать в виде матрицы:

.

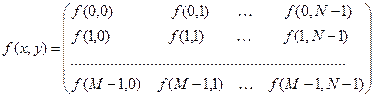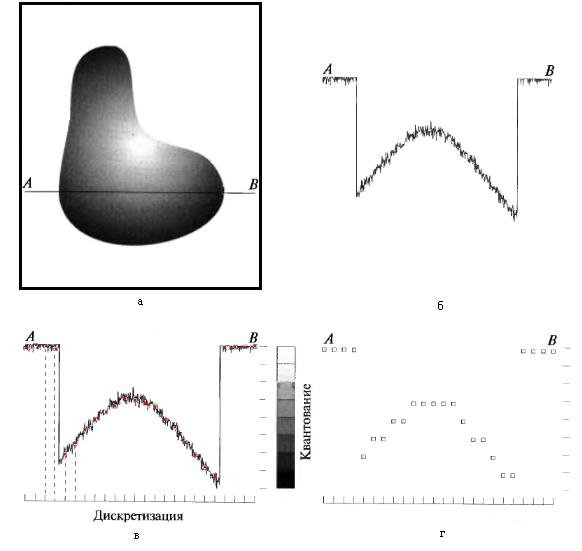
Рис.1.3. Формирование ЦИ. Непрерывное изображение (а). Профиль вдоль линии сканирования между точками А и В на непрерывном изображении, который используется для иллюстрации понятий дискретизация и квантование (б). Дискретизация и квантование (в). Цифровое представление строки изображения (г).

Каждый элемент этой матрицы – элемент изображения или пиксель. Далее будем использовать более традиционную матричную запись:

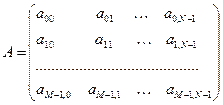
Для выполнения процесса оцифровки изображения необходимо принять решение относительно значений М и N, а также числа уровней (градаций) яркости L, разрешенных для каждого пикселя. Для М и N не существует специальных требований помимо того, что они должны быть натуральными. А значение L, по соображениям удобства построения оборудования для обработки, хранения и дискретизации, обычно выбирают 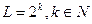, где 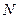- множество натуральных чисел. Мы предполагаем, что дискретные уровни яркости расположены с постоянным шагом (т.е. используется равномерное квантование) и принимают целые значения в интервале 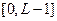. Интервал значений яркости называют динамическим диапазоном изображения.

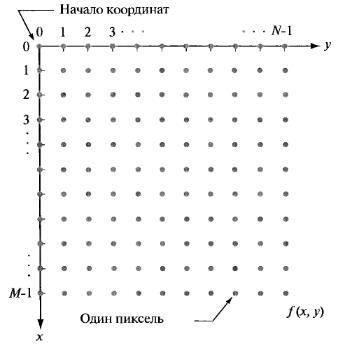
Рис.1.4. Система координат для представления цифровых изображений

Дискретизация является главным фактором, определяющим пространственное разрешение изображения. По существу, пространственное разрешение – это размер мельчайших различимых деталей на изображении.

Яркостным или полутоновым разрешением называется мельчайшее различимое изменение яркости. При выборе числа градаций яркости приходится в значительной степени учитывать особенности аппаратуры. Наиболее частым является выбор 8-битного представления (256 градаций серого) .

В качестве очень грубого эмпирического правила можно считать, что минимальные пространственное и яркостное разрешение, при котором ЦИ будет относительно свободным от дефектов типа ложных контуров и ступенчатости, составляет около 256*256 пикселей с 64 градациями яркости.