С ЗАДАННЫМ РАДИУСОМ И СКОРОСТЬЮ РАЗВОРОТА

Задача решается по формулам:

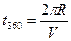
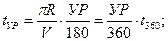
где π = 3,14;

R — радиус разворота в км или м;

V — скорость разворота в км/час или м/сек;

УР — угол разворота самолета.

Порядок решения (шкалы 1 и 2):

— установить визирку по шкале 1 на деление, соответствующее скорости полета самолета V в км/час (рис. 49);

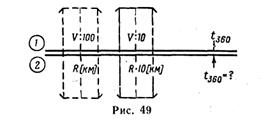
— передвигая движок, подвести под визирку деление шкалы 2, соответствующее радиусу разворота R;

— отсчитать по шкале 2 против индекса t₃₆₀искомое время разворота самолета на 360°.

Примеры.Дано: 1) V = 700 км/час; R = 8,5 км. Находим: t₃₆₀= 4 мин. 35 сек.

2) Дано: V = 450 км/час; R = 6,5 км. Находим: t₃₆₀ = 5 мин. 26 сек.

3) Дано: V = 240 км/час; R = 1500 м. Находим: t₃₆₀ — 2 мин. 22 сек.

Примечания: 1. При радиусе разворота до 10 км скорость уменьшать в 10 раз и устанавливать на втором интервале шкалы 1; радиус разворота увеличивать в 10 раз и устанавливать на втором интервале шкалы 2.

2. При радиусе разворота более 10 км скорость уменьшать в 100 раз и устанавливать на первом интервале шкалы 1, а радиус разворота в км устанавливать на первом интервале шкалы 2.

Для определения времени разворота на любой угол необходимо:

— определить время разворота на 360°, как указано выше;

— установить визирку по шкале 1 наделение, соответствующее значению 360 (рис. 50);

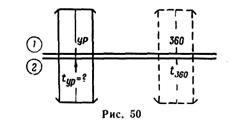
— передвигая движок, подвести под визирку по шкале 2 значение времени разворота самолета на 360°;

— установить визирку по шкале 1 на величину угла разворота самолета;

— отсчитать по шкале 2 искомое значение времени разворота на заданный угол.

Пример.Дано: t₃₆₀ — 5 мин. 35 сек.; УР = 125°. Находим: t_УР= 1 мин. 56 сек.