Магнитное поле и его характеристики. Закон Ампера.
Опыт показывает, что, подобно тому, как в пространстве, окружающем электрические заряды возникает электрическое поле, в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, которое называется магнитным.
Источники магнитного поля:
1) проводники с током; 2) намагниченные тела; 3) переменное электрическое поле.
Идеальные модели:
1) движущийся электрический точечный заряд qV  (V– скорость);
(V– скорость);
2) Элемент тока Idl, где. dl – длина участка проводника, направление которого совпадает с направлением тока.
Силовая характеристика магнитного поля В – вектор магнитной индукции. Помещенный в какую-либо точку поля «пробный» элемент тока Idlиспытывает действие силы:
dF = [Idl, B].(4.1) В скалярной форме dF = Idl B sin α.
Если α = π/2, то Idlперпендикулярно вектору В, а значит dF максимальна. Таким образом:
 – (4.2)
– (4.2)
определение силовой характеристики магнитного поля В.Единица магнитной индукции – Тесла: 1 Тл = 1 Н/(А∙м).
Формула (4.1) – закон Ампера, dF– сила Ампера.
Если В =const – поле однородное. Направление dF находится по правилу векторного произведения – правилу левой руки (правило буравчика) (рис.4.1).
Магнитная сила dFне является центральной, т.е. не является консервативной.
Графически магнитное поле изображается в виде линий В– силовых линий магнитного поля (рис. 4.2). Это такие линии, которые проводятся так, чтовекторВв каждой точке силовой линии направлен по касательной к ней.Направлениесиловых линий и вектора В определяется поправилу буравчика.
 Линии В не имеют начала и конца,таккакне существует магнитных зарядов.
Линии В не имеют начала и конца,таккакне существует магнитных зарядов.
Линии Влибо замкнуты, либо идут из ∞ в ∞, либо бесконечно навиваются на некоторую поверхность, всюду плотно заполняя ее, но никогда не возвращаясь вторично в любую точку поверхности.
4.2. Поле точечного заряда, движущегося с V=const и V<< c
(нерелятивистский случай)
Этот закон получен из экспериментальных данных:

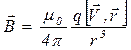 , (4.3)
, (4.3)
где r– радиус-вектор, проведенный от заряда q к точке наблюдения, µ0 – магнитная постоянная = 4π.10-7 Гн/м.
Закон (4.3) в скалярном виде:
 ,
,
где α – угол между векторами Vи В.
Дата добавления: 2015-09-18; просмотров: 1149;
