Электроемкость
1)Электроемкость уединенного проводника (т.е. удаленного от других проводников, тел и зарядов).
Из опыта следует что q ~ φ,т.е. q = Cφ;
С–коэффициент пропорциональности.
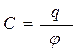 . (1.6)
. (1.6)
Электроемкость уединенного проводника численно равна заряду, сообщение которого проводнику повышает его потенциал на единицу. С зависит от размеров и формы проводника.
Пример. Расчет электроемкости С уединенного шара (сферы) радиуса R.
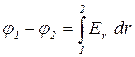 , отсюда
, отсюда 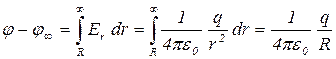
Подставив полученное выражение в формулу (1.6), получим С=4πε0R.
Электроемкость в системе СИ измеряется в фарадах (Ф); 1 Ф = 1Кл/1В. Фарад – очень большая величина. Поэтому на практике электроемкость С измеряют в мкФ (10-6 Ф), пФ (10-12 Ф).
2) Электроемкость конденсаторов.
При приближении к проводнику других тел его электроемкость существенно увеличивается. Это обусловлено явлением электростатической индукции.
Пусть заряд проводника q > 0, тогда на других телах возникают индуцированные заряды, причем отрицательные оказываются ближе к проводнику, нежели положительные.
Используя принцип суперпозиции φ = ∑φi, потенциал проводника уменьшается при приближении к нему незаряженных тел:
φ = φ0 – φ′_ + φ′+ ,
где φ0 – потенциал проводника,φ′_и φ′+ –потенциалы индуцированных зарядов на других телах.
|φ′_| >|φ′+|,т.к. (-q′)находится ближе к проводнику.
Так как 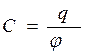 , то электроемкость конденсатора увеличится. Это позволило создать систему проводников, которая обладает электроемкостью C значительно большей, чем уединенный проводник, причем не зависящей от окружающих тел. Такая система называется конденсатором.
, то электроемкость конденсатора увеличится. Это позволило создать систему проводников, которая обладает электроемкостью C значительно большей, чем уединенный проводник, причем не зависящей от окружающих тел. Такая система называется конденсатором.
Простейший конденсатор состоит из двух проводников (обкладок), расположенных на малом расстоянии друг от друга.
Чтобы внешние тела не влияли на электроемкость С конденсатора, его обкладки располагают так, чтобы поле было сосредоточено практически полностью внутри конденсатора. Это означает, что линии Е, начинающиеся на одной обкладке, заканчиваются на другой, т.е. заряды должны быть одинаковы по величине и противоположны по знаку (q и –q).
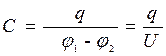 ,
,
где φ1 – φ2 = U– совпадает с напряжением.
а) Электроемкость плоского конденсатора
Плоский конденсатор состоит из двух параллельных пластин, разделенных зазором шириной d.
 Напряженность между обкладками
Напряженность между обкладками
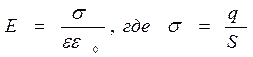 ; S – площадь каждой пластины.
; S – площадь каждой пластины.
Разность потенциалов между обкладками
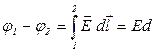 , без учета краевых эффектов. U = Ed – напряжение между обкладками. Следовательно,
, без учета краевых эффектов. U = Ed – напряжение между обкладками. Следовательно,
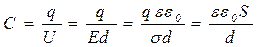 .
.
Таким образом, электроемкость плоского конденсатора:
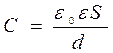 . (1.7)
. (1.7)
Емкость реального конденсатора определяется полученным выражением тем точнее, чем меньше зазор d по сравнению с линейными размерами пластин.
б) Соединения конденсаторов
Для получения конденсатора заданной электроемкости нет необходимости каждый раз изготавливать новый образец. Необходимого результата добиваются, используя различные типы соединения конденсаторов, имеющихся в наличии.
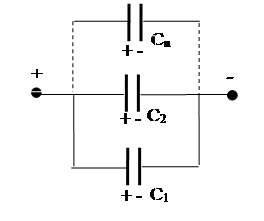 1.Параллельное соединение конденсаторов – соединение, при котором все конденсаторы подключены между собой одной и той же парой точек (узлами).
1.Параллельное соединение конденсаторов – соединение, при котором все конденсаторы подключены между собой одной и той же парой точек (узлами).
U1=U2 =… =U=const.
Полный заряд равен сумме зарядов отдельных конденсаторов:
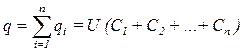 .
.
Отсюда, C = ∑Ci (1.8)
т.е. полная емкость равна сумме емкостей отдельных конденсаторов.
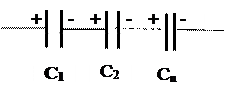 2.Последовательное соединение конденсаторов.
2.Последовательное соединение конденсаторов.
Значение заряда на каждом конденсаторе одно и то же:
q1 = q2 = … = qn = q = const.
Общее напряжение равно сумме напряжений на отдельных конденсаторах:
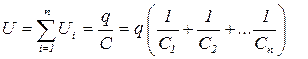 . (1.9)
. (1.9)
Таким образом, 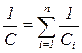 .
.
При последовательном соединении полная емкость меньше самой малой емкости используемых конденсаторов.
Формулы (1.8) и (1.9) применяют не только для расчета емкости батареи конденсаторов, но и для определения емкости многослойных конденсаторов.
При смешанном соединении конденсаторов, последовательно применяют эти формулы.
Дата добавления: 2015-09-18; просмотров: 1667;
