Закон Джоуля-Ленца
10.4.1.Закон Джоуля-Ленца в диференціальній формі
У класичній моделі електричного струму приймається, що при співударянні з розсіюючим центром носій струму зупиняється, тобто повністю передає середовищу придбану за рахунок роботи поля кінетичну енергію 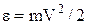 . Якщо t ¾ час вільного пробігу носія струму, то за одиницю часу носій здійснить N не пружних співударянь із решіткою
. Якщо t ¾ час вільного пробігу носія струму, то за одиницю часу носій здійснить N не пружних співударянь із решіткою
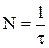 . (1)
. (1)
При цьому одиниці об'єму середовища за одиницю часу буде передана енергія
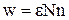 , (2)
, (2)
де n ¾ концентрація носіїв струму провідника. Підставляючи у (2) вираз для максимальної швидкості 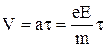 , отримаємо
, отримаємо
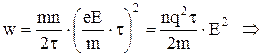
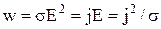 . (3)
. (3)
Вираз (3) визначає густину теплового потоку у провіднику і носить назву диференціального закону Джоуля-Ленца.
10.4.2.Закон Джоуля-Ленца в інтегральній формі
З диференціального закону можна одержати інтегральний закон Джоуля-Ленца для теплового потоку. Дійсно, якщо в провіднику йде струм І, то величина dQ розсіяної енергії в елементі об'єму провідника за час dt може бути розрахована так
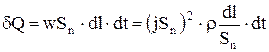 (4)
(4)
і після інтегрування по ділянці провідника довжиною L одержимо
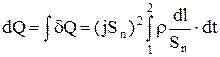 (5)
(5)
У (5) 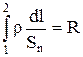 ¾ опір ділянки 1¾2 провідника,
¾ опір ділянки 1¾2 провідника, 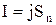 ¾ струм у провіднику. І остаточно одержимо
¾ струм у провіднику. І остаточно одержимо
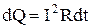 . (6)
. (6)
Величина 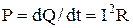 називається тепловим потоком у провіднику і чисельно потік дорівнює потужності джерела струму, яка виділяється у провіднику.
називається тепловим потоком у провіднику і чисельно потік дорівнює потужності джерела струму, яка виділяється у провіднику.
Вираз (6) Джоуль та Ленц установили експериментально і його називають інтегральним законом Джоуля-Ленца.
10.5. Температурна залежність опору провідника
Фізичний зміст опору R провідника можна установити з виразу j=enVд, де величина заряду е та концентрація n є сталими величинами. Збільшення чи зменшення струму відбувається при зменшенні чи збільшенні дрейфової швидкості V. При сталій напруженості поля у провіднику зміна величини V спостерігається при зміні його температури. При збільшенні температури, за рахунок збільшення інтенсивності розсіювання направленого руху зарядів тепловими коливаннями вузлів кристалічної, відбувається зменшення V і навпаки. Тобто опір електричному струмові у провіднику збільшується із збільшенням температури провідника і навпаки. Експеримент показує, що для високих температур питомий опір металів залежить від температури лінійно
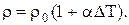 (1)
(1)
У цьому виразі 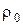 ¾ питомий опірпри
¾ питомий опірпри 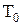 = 273,15 К,
= 273,15 К, 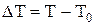 ,
, 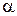 ¾ температурний коефіцієнт опору.
¾ температурний коефіцієнт опору.
Основним недоліком класичної теорії провідності є те, що вона не може дати реальну залежність опору провідника від його температури (1). Дійсно, якщо класичний вираз для середньої теплової швидкості 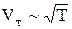 , то
, то 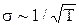 , а
, а 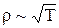 , що суперечить експериментові. Цей недолік класичної теорії електропровідності пов¢язаний з тим, що за шлях вільного направленого пробігу l, що здійснюється під дією електричного поля, приймають середню довжину вільного пробігу теплового руху l. Експеримент показує, що класичне значення провідності можна отримати, допустивши середню довжину вільного пробігу l¢ рівною сотням міжвузольних відстаней кристалічної решітки металу.
, що суперечить експериментові. Цей недолік класичної теорії електропровідності пов¢язаний з тим, що за шлях вільного направленого пробігу l, що здійснюється під дією електричного поля, приймають середню довжину вільного пробігу теплового руху l. Експеримент показує, що класичне значення провідності можна отримати, допустивши середню довжину вільного пробігу l¢ рівною сотням міжвузольних відстаней кристалічної решітки металу.
В 1911 році голландський інженер Камерлінг-Оннес відкрив явище надпровідності, яке полягає у тому, що при температурах менших 4К ртуть втрачає електричний опір. Таке охолодження ртуті було досягнуте за допомогою рідкого гелію. За відкриття явища надпровідності у 1913 році Камерлінг-Оннес був відзначений Нобілевською премією.
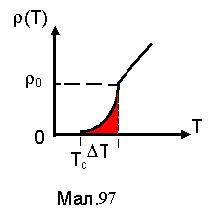 Явище надпровідностібуло зафіксовано при гелійових температурах у ряду металів та сплавів ¾ Pb, Zn, Al, вісмут із золотом та інші. На Мал.97 зображена залежність питомого опору металу (сплаву) від температури. На графіку
Явище надпровідностібуло зафіксовано при гелійових температурах у ряду металів та сплавів ¾ Pb, Zn, Al, вісмут із золотом та інші. На Мал.97 зображена залежність питомого опору металу (сплаву) від температури. На графіку 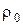 ¾ залишковий опір звичайного стану,
¾ залишковий опір звичайного стану, 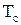 ¾ температура надпровідності, нижче якої опір матеріалу дорівнює 0. Існує скінчений інтервал температури перехідної області
¾ температура надпровідності, нижче якої опір матеріалу дорівнює 0. Існує скінчений інтервал температури перехідної області 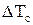 від звичайного стану до стану надпровідності. Для чистих надпровідників DТс»10-3 К. Про характер опору електричному струму надпровідника говорить той факт, що струм, створений за рахунок електромагнітної індукції у кільцевому надпровіднику, може існувати роками.
від звичайного стану до стану надпровідності. Для чистих надпровідників DТс»10-3 К. Про характер опору електричному струму надпровідника говорить той факт, що струм, створений за рахунок електромагнітної індукції у кільцевому надпровіднику, може існувати роками.
10.6. Сторонні сили, ЕРС
При сполученні тіл із різними потенціалами провідником у ньому за рахунок кулонівських сил 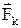 виникає спадний у часі струм, що приводить до вирівнювання потенціалів і подальшого припинення струм у провіднику. Для підтримки в електричному колі струму певної величини, необхідно щоб у ньому, крім кулонівських, існували б ще й інші сили, що підтримують певну різницю потенціалів. Ці сили називаються стороннімиі їх призначенням є розділ різнойменних зарядів, для створення електричного поля. Усередині джерела сторонніх сил виконується робота по перенесенню зарядів проти сил електростатичного поля. Ділянка кола, на якій існують сторонні сили
виникає спадний у часі струм, що приводить до вирівнювання потенціалів і подальшого припинення струм у провіднику. Для підтримки в електричному колі струму певної величини, необхідно щоб у ньому, крім кулонівських, існували б ще й інші сили, що підтримують певну різницю потенціалів. Ці сили називаються стороннімиі їх призначенням є розділ різнойменних зарядів, для створення електричного поля. Усередині джерела сторонніх сил виконується робота по перенесенню зарядів проти сил електростатичного поля. Ділянка кола, на якій існують сторонні сили 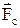 називається неоднорідною. На цій ділянці на пробний заряд
називається неоднорідною. На цій ділянці на пробний заряд 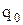 діють сили
діють сили
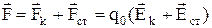 ,(1)
,(1)
де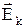 ¾напруженість кулонівських сил,
¾напруженість кулонівських сил,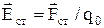 ¾напруженість поля сторонніх сил. Робота кулонівських та сторонніх сил на ділянці електричного кола 1¾2 запишеться у вигляді
¾напруженість поля сторонніх сил. Робота кулонівських та сторонніх сил на ділянці електричного кола 1¾2 запишеться у вигляді
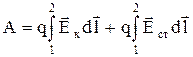 .(2)
.(2)
Відношення А/q називається напругоюU на ділянці кола 1¾2 із джерелом сторонніх сил
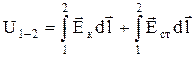 .(3)
.(3)
Перший інтеграл є різниця потенціалів
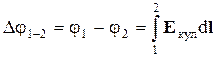 ,(4)
,(4)
а другий інтеграл визначає електрорушійну силу(ЕРС) джерела струму
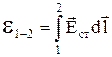 ,(5)
,(5)
яка чисельно дорівнює роботі сторонніх сил по перенесенню одиничного заряду на ділянці 1¾2 електричного кола. Таким чином напругу на неоднорідній ділянці кола можна записати у вигляді
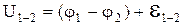 .(6)
.(6)
В загальному випадку, під напруженістю поля завжди слід розуміти відношення 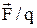 , де у
, де у 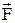 враховані сторонні сили. Наприклад, у диференціальному законі Ома треба писати
враховані сторонні сили. Наприклад, у диференціальному законі Ома треба писати
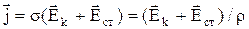 .(7)
.(7)
В (7) можна утворити таке співвідношення
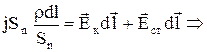
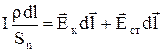 ,(8)
,(8)
де 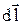 ¾ елемент струму,
¾ елемент струму, 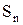 ¾ поперечний переріз провідника. Якщо у (8) провести інтегрування лівої й правої частин по ділянці кола 1 ¾ 2, то в лівій частині виразу одержимо опір
¾ поперечний переріз провідника. Якщо у (8) провести інтегрування лівої й правої частин по ділянці кола 1 ¾ 2, то в лівій частині виразу одержимо опір
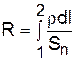
ділянки кола помножений на струм І=(j Sn), а в правій частині ¾ напругу (6), тобто
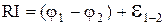 .
.
Одержана формула виражає закон Ома для неоднорідної ділянки кола ¾ ділянки, яка містить джерело сторонніх сил.
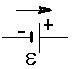 Джерело сторонніх сил
Джерело сторонніх сил 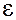 графічно представляється так, як вказано на малюнку. Стрілкою
графічно представляється так, як вказано на малюнку. Стрілкою
Де знак "-" означає від'ємний полюс, а знак "+" ¾ додатній полюс.
10.7. Правила Кірхгофа
Кірхгоф установив правила розв'язку задач для розгалуженого електричного кола. Розгалуженим електричним колом називається коло, в якому є 2 і більше вузлів струму. Вузол ¾ це точка з'єднання кола, де сходяться 3 і більше струмів. Наприклад, на Мал.98 представлено вузол у точці Y в яку входять струми І1 та І3 , а виходять струми І2 та І4.
10.7. 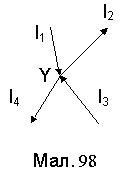 1.Перше правило Кірхгофа
1.Перше правило Кірхгофа
Для сталого або квазисталого струму у вузлах не відбувається накопичення зарядів і виконується закон збереження заряду. Звідси випливає перше правило Кірхгофа: сума струмів, що приходять у вузол, дорівнює сумі струмів, що виходять із вузла. Якщо струмам, що виходять із вузла приписати від'ємний знак, а струмам, що входять ¾ додатний, то перше правило Кірхгофаможна записати у вигляді
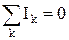 , (1)
, (1)
де алгебраїчна сума береться по всім k струмам вузла. Для наведеного на малюнку 98 прикладу, за першим правилом Кірхгофа буде
І1 + І3 - І2 - І4 = 0.
10.7.2.Друге правило Кірхгофа
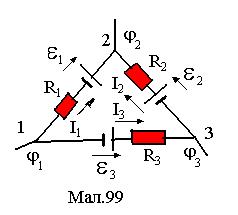 В розгалужених колах виділяються окремі замкнені контури, вершинами яких є вузли. Кожна зі сторін контуру розглядається як неоднорідна дільниця струму з потенціалами jі та jі+1, струмом Іі, опором Rі, електрорушійною силою Еі та напругою Uі=RіІі. За додатній прийнято напрямок обходу контуру проти годинникової стрілки, тобто напрямок 1¾3¾2 для прикладу, зображеного на малюнку 99. Виведемо 2-е правило Кірхгофа. Запишемо вирази для напруги на ділянках 1,2, 3 :
В розгалужених колах виділяються окремі замкнені контури, вершинами яких є вузли. Кожна зі сторін контуру розглядається як неоднорідна дільниця струму з потенціалами jі та jі+1, струмом Іі, опором Rі, електрорушійною силою Еі та напругою Uі=RіІі. За додатній прийнято напрямок обходу контуру проти годинникової стрілки, тобто напрямок 1¾3¾2 для прикладу, зображеного на малюнку 99. Виведемо 2-е правило Кірхгофа. Запишемо вирази для напруги на ділянках 1,2, 3 :
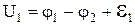
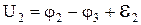
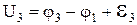
Якщо додати ліві та праві частини записаних рівностей, то в правій частині послідовно взаємознищуються потенціали j і в результаті одержимо 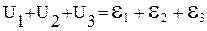 . Одержана рівність
. Одержана рівність

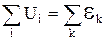 (2)
(2)
виражає друге правило Кірхгофа. В (2) напруги беруться із знаком "+", якщо відповідні їм струми за напрямком співпадають із напрямком обходу контуру, а в противному їм приписується знак "-". За додатній напрямок ЕРС береться напрямок від полюса "-" до полюса "+", як це показано на малюнкові. Знак ЕРС у правій частині (2) визначається співпаданням напрямку ЕРС із напрямком обходу (знак "+"), чи ні (знак"-"). За законом Ома Uі = ІіRі і друге правило Кірхгофа можна записати також у вигляді
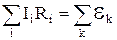 . (3)
. (3)
10.7.3.Розв'язок електротехнічних задач на основі правил Кірхгофа.
Методика розв'язування цих задач полягає в тому, що в розгалужених колах виділяються вузли й окремі замкнені контури. Указується додатній напрям обходу контурів: проти годинникової стрілки. Далі визначаються струми та ЕРС і їх напрями на кожній зі сторін контуру. Знаки струмів та ЕРС додатні, якщо їх напрямки співпадають із напрямком обходу контуру. Для вузлів записують перше, а для контурів друге правило Кірхгофа. Таким чином можна одержати необхідну систему незалежних лінійних рівнянь відносно невідомих опорів R, струмів І та ЕРС.
10.8. Електропровідність рідин
Носіями струму в рідинах є іони. До таких рідин відносяться ті, що
мають вільні заряди ¾ йони, утворені внаслідок дисоціації молекул. Під дисоціацією розуміють розпад під впливом розчинника молекули на додатній (аніон) та від'ємний (катіон) йони, які мають рівні за величиною заряди. Електролітична дисоціація відбувається при розчиненні кислоти, солі або лугу в результаті взаємодії молекул цих речовин із полярними молекулами води чи інших розчинників, які мають значний дипольний момент. Унаслідок хаотичного теплового руху іонів, відбувається також зворотний дисоціації процес ¾ молізація, при якому знову утворюється нейтральна молекула. В умовах динамічної рівноваги дисоціації та молізації електроліт характеризується коефіцієнтом дисоціації a, який дорівнює відношенню числа дисоційованих молекул до їх загального числа в розчині.
Як відомо, зв'язок іонних молекул між собою здійснюється через валентні електрони, число яких позначимо через Z. Ці електрони сприймаються одним чи декількома атомами в результаті чого одна з груп атомів стає додатнім іоном, а інша від'ємним іоном. Таким чином заряд іона можна записати у вигляді q=Ze, де 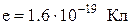 . Через М позначимо молярну масу іона виражену в атомних одиницях маси
. Через М позначимо молярну масу іона виражену в атомних одиницях маси 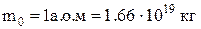 .
.
При створенні в електроліті електричного поля напруженості Е, іони починають направлений упорядкований рух із дрейфовою швидкістю V, яка, як і в металах, пропорційна напруженості поля Е, причому 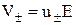 , де знаки
, де знаки 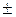 відносяться до додатних та від'ємних іонів відповідно, а
відносяться до додатних та від'ємних іонів відповідно, а 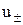 ¾ їх рухливості. Вираз для густини струму можна записати у вигляді
¾ їх рухливості. Вираз для густини струму можна записати у вигляді
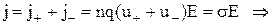
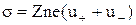 , (1)
, (1)
де n концентрація іонів, s ¾ провідність. Рухливість u± у першому наближенні не залежить від напруженості поля, а визначається природою іона, температурою, в'язкістю та іншими характеристиками електроліту.
При проходженні струму І через електроліт відбувається перенос маси речовини. При цьому на електродах виділяється N іонів відповідної речовини із зарядом Q. Маса речовини пропорційна величині заряду Q=Іt=Nq=NZe, що пройшов за час t
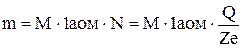 . (2)
. (2)
Якщо чисельник та знаменник помножити на число Авогадро Na=6.022×1023 моль-1, то в чисельнику одержимо молярну масу речовини
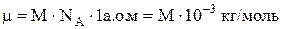 ,
,
а в знаменнику універсальну сталу Фарадея
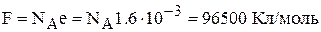 . (3)
. (3)
Як видно з (3) число Фарадея F чисельно дорівнює заряду моля електронів. Тепер вираз для маси може бути записано у вигляді
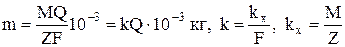 .
.
Коефіцієнт к називається електрохімічним еквівалентоміона, а коефіцієнт kх називається хімічним еквівалентоміона.
10.9. Електропровідність газів
Класична модель електропровідності газів виходить із того, що його нейтральні атоми чи молекули в певних процесах іонізуються. Ці процеси можуть передувати або відбуватися рівночасно із створенням в об'ємі газу електричного поля. Іонізація передбачає виконання деяким джерелом роботи А на виривання електронів із зовнішніх (валентних) орбіталей атомів, що входять до складу газу. Для характеристики здатності частинок газу іонізуватися, вводиться поняття потенціалу іонізації 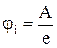 , де е ¾заряд електрона.
, де е ¾заряд електрона.
Таблиця. Потенціали іонізації деяких речовин.
| Атоми | H | He | O | N | Ne | Cl | Na | Hg | K | Ar |
| jі,еВ | 13.6 | 24.6 | 13.6 | 14.5 | 21.6 | 13.0 | 5.14 | 10.4 | 4.34 | 15.8 |
| молекули | H2 | O2 | H2O | N2 | NO2 | Cl2 | CO2 | CO | HCl | NO |
| jі,еВ | 15.4 | 12.2 | 12.6 | 15.6 | 12.3 | 11.3 | 13.8 | 14.0 | 12.6 | 9.2 |
Кількісною характеристикою процесу іонізації є інтенсивність іонізації, яка визначається числом новоутворених пар різнойменних зарядів за одиницю часу. Найуживанішим процесом іонізації є ударна іонізація. В електричному полі деяка заряджена частинка, наприклад, електрон, розганяється до певних енергій і співударяється з частинкою газу. При іонізації це зіткнення носить характер не пружного удару. Запишемо закон збереження імпульсу для не пружного удару
mV = (m + M)u, (1)
де М ¾ маса атома, m ¾ маса ударної частинки, а V ¾ її швидкість, u ¾ швидкість частинки та атома після не пружного удару. Кінетична енергія частинки витрачається на роботу іонізації Aі та створення кінетичної енергії атома й частинки Mu2/2
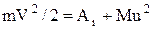 . (2)
. (2)
Підстановка значення u із (1) у (2) дає
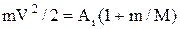 . (3)
. (3)
Звідси видно, що енергія частинки не може бути менша за роботу іонізації та вона буде тим ближча до Аі, чим менша її маса m, порівнюючи з масою атома М. Таким чином ударна іонізація можлива при виконанні умови
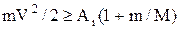 . (4)
. (4)
Рівночасно з процесом іонізації відбувається зворотній процес ¾ процес рекомбінації іонів та електронів ¾ перетворення іонів у нейтральні атоми чи молекули.
Плазма
Привисоких температурах речовина переходить у стан, який називається плазмою. Плазма¾ іонізований газ, у якому об'ємні густини додатних r+ та від'ємних r- зарядів однакові за величиною, його об'єм значно більший характерного об'єму D3, у якому спостерігається порушення рівноваги числа додатних та від'ємних зарядів. Величина D називається Дебаєвським радіусомекрануванняі залежить від температури плазми 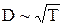 . Фізичним змістом Дебаєвського радіуса екранування є те, що на відстанях більших за D від іона чи електрона їх електростатичне поле екранується повністю.
. Фізичним змістом Дебаєвського радіуса екранування є те, що на відстанях більших за D від іона чи електрона їх електростатичне поле екранується повністю.
Плазма називається ідеальною або газовою, якщо енергія електростатичної взаємодії двох заряджених частинок плазми на середній відстані < r > значно менша теплової енергії Е=кТ. Така плазма має властивості ідеального газу і добре описується рівнянням
p = nkT.
Відношення числа іонізованих атомів до їх загального числа у плазмі називається ступенем іонізації плазми.
Утворення плазми відбувається за рахунок термічних процесів ( 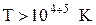 ), ударної іонізації, фотоіонізації. За рахунок великої електропровідності, плазма сильно взаємодіє із зовнішніми електричними та магнітними полями. Взаємодія між частинками усередині плазми відбувається за рахунок далекодії кулонівських сил і носить колективний, а не парний характер. В цьому відношенні плазма має властивості пружного середовища, в якому збуджуються й розповсюджуються коливання в тому числі й коливання об'ємного заряду, так звані ленгмюлерівські коливання плазми.
), ударної іонізації, фотоіонізації. За рахунок великої електропровідності, плазма сильно взаємодіє із зовнішніми електричними та магнітними полями. Взаємодія між частинками усередині плазми відбувається за рахунок далекодії кулонівських сил і носить колективний, а не парний характер. В цьому відношенні плазма має властивості пружного середовища, в якому збуджуються й розповсюджуються коливання в тому числі й коливання об'ємного заряду, так звані ленгмюлерівські коливання плазми.
Плазма ¾ найбільш розповсюджений стан речовини у Всесвіті. Він утворюється за рахунок термоядерних реакцій синтезу усередині зірок, фотоіонізації у холодних туманностях та міжзоряному просторі. Радіаційні пояси Землі є також плазмою. Низькотемпературна плазма має широке застосування в прикладних областях: джерелах денного світла, реактивних двигунах, для зварювання та різання металів. Найбільші надії пов'язуються із створенням керованих термоядерних реакторів, де основним робочим середовищем є плазма з високою температурою та густиною.
10.11. Контактні та термоелектричні явища в металах
Метал являє собою кристалічну решітку. При утворенні кристала атоми зближаються на такі відстані, що відбувається перекриття зовнішніх (валентних) та внутрішніх електронних орбіталей. При цьому перекриття валентних орбіталей настільки значне, що валентні електрони сколективізуються у газ "вільних" електронів: кожен із них наче належить всім атомам рівночасно. У вузлах кристалічної решітки розміщуються іонізовані таким чином атоми. Вони здійснюють тепловий коливальний рух. Вільні електрони можуть рухатися у періодичному полі кристала під дією зовнішнього електричного поля. Тому вони мають ще назву електронів провідності.
Дата добавления: 2015-09-18; просмотров: 1175;
