Схемы замещений КЛ для напряжений 10-220 кВ
Кабельные линии электропередачи представляют такой же П-образной схемой замещения как и ВЛ.
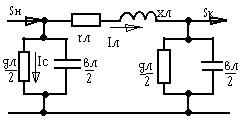
Удельные активные и реактивные сопротивления r0, х0 определяют по справочным таблицам, так же как и для ВЛ.
Из выражения для х0 и в0
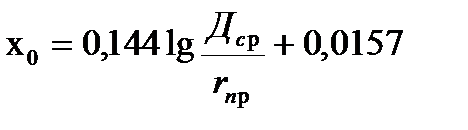
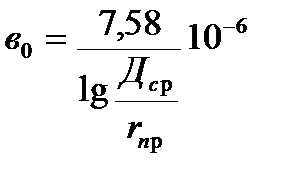
видно, что х0 уменьшается, а в0 растет при сближении разных проводов.
Для кабельных линий расстояние между проводами фаз значительно меньше, чем для ВЛ и Х0 очень мало.
При расчетах режимов КЛ (кабельных линий) напряжением 10кВ и ниже можно учитывать только активное сопротивление.
| rл |
Емкостный ток и Qс в кабельных линиях больше чем в ВЛ. В кабельных линиях (КЛ) высокого напряжения учитывают Qс, причем удельную емкостную мощность Qc0 кВАр/км можно определить по таблицам в справочниках.
Активную проводимость (gл )учитывают для кабелей 110 кВ и выше.
Удельные параметры кабелей х0, а также Qс0 приведенные в справочных таблицах ориентировочны, более точно их можно определить по заводским характеристикам кабелей.
Задания для самостоятельной работы:
1. Выбор проводов ЛЭП.
2. Составление схемы замещения электрической сети: генератор-двухобмоточный трансформатор-линия- двухобмоточный трансформатор-нагрузка.
Лекция 5. Характерные соотношения между параметрами ЛЭП. Расчет режимов ЛЭП при заданном токе и напряжении в конце линии. Векторные диаграммы.
5.1. Характерные соотношения между параметрами
ЛЭП. Транспозиция проводов
Активное сопротивление проводов и кабелей определяется материалом токоведущих жил и их сечениями.
С изменением сечения проводов и кабелей значительно изменяются их активные сопротивления.
Активное сопротивление обратно пропорционально сечению провода или кабеля.
Магнитное поле возникающее вокруг и внутри проводов ВЛ и жил кабелей определяет их индуктивное сопротивление. Индуктивное сопротивление зависит от взаимного расположения проводов.
Индуктивные сопротивления фазных проводов ВЛ будут одинаковыми, если они расположены по вершинам равностороннего треугольника, и будут отличаться друг от друга, если фазные провода подвешиваются в горизонтальной плоскости. Чтобы избежать нежелательной несимметрии применяют транспозицию проводов, которая заключается в том, что в нескольких точках линии фазные провода на опорах меняются местами. При этом каждый провод поочередно занимает все три возможные положения при примерно одинаковой протяженности.
Благодаря транспозиции, эдс, наводимые в фазных проводах выравниваются и индуктивные сопротивления становятся одинаковыми.
Для иллюстрации приведем пример индуктивных сопротивлений трех напряжений для средних сечений проводов и расстояний между проводами:
1) линия 6,10 кВ х0=0,362 Ом/км;
2) линия 35 кВ х0=0,401 Ом/км;
3) линия 110 кВ х0=0,433 Ом/км.
При выполнении ВЛ одиночными (нерасщепленными проводами) их индуктивное сопротивление: х0»0,4 Ом/км.
Индуктивное сопротивление расщепленных проводов, вследствие увеличения эквивалентного радиуса, будет меньше и при расщеплении на три провода будет х0»0,29 Ом/км.
Малая зависимость от конструктивных характеристик ВЛ также присуща и емкостной проводимости.
Среднее значение проводимости для ВЛ , выполненной одиночными проводами во ср»2,75´10-6 См/км.
Для линий с расщепленными проводами емкостная проводимость увеличивается и при расщеплении на три провода: в0»3,8´10-6См/км.
Для линий 110кВ при характерной для них протяженности зарядная мощность QC»10% от передаваемой;
Для линий 220кВ 30% от передаваемой;
Для линий 500кВ может быть соизмерима с передаваемой активной мощностью.
Для линий 35кВ и более низким направлением зарядную мощность можно не учитывать.
5.2. Расчет режима ЛЭП при заданном токе нагрузки и
напряжении в конце линии
Связь между изменяющимися величинами определяется с помощью диаграмм, в которых каждая из величин характеризуется вектором. Построим диаграмму, показывающую соотношения между токами и напряжениями П-образной схемы замещения.
Будем считать, что режим конца линии задан фазным напряжением Uф=сonst и отстающим током нагрузки I2. Также заданы Z12=r12+jx12, в12.
Необходимо определить 1) напряжение в начале линии – U1,2) ток в продольной части – I12, 3) потери мощности - DS12 4) ток в начале линии – I1.
| U1 |
| U2 |
| I1 |
| I2 |
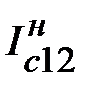
|
|
| r12 |
| x12 |
| I12 |
Расчет состоит в определении неизвестных токов и напряжений, последовательно от конца линии к началу.
Емкостный ток в конце линии 1-2, по закону Ома:
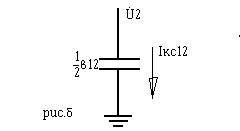
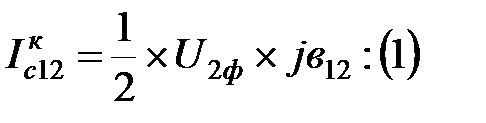
Ток в продольной части линии 1-2, по первому закону Кирхгофа:
I12=I2+Iкс12: (2)
Напряжение в начале линии по закону Ома:
U1ф=U2ф+I12´Z12: (3)
Емкостный ток в начале линии:
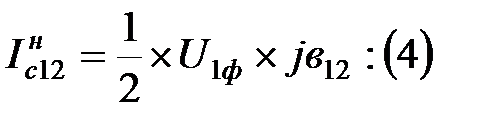
Ток в начале линии по первому закону Кирхгофа:
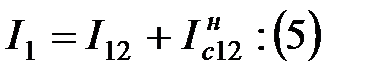
Потери мощности в линии (в трех фазах):
DS12=3I212´Z12: (6)
5.3. Векторная диаграмма для расчета режима ЛЭП при заданном
токе нагрузки и напряжении в конце линии для линии с нагрузкой
Векторная диаграмма токов и напряжений строится в соответствии с выражениями 1-5.
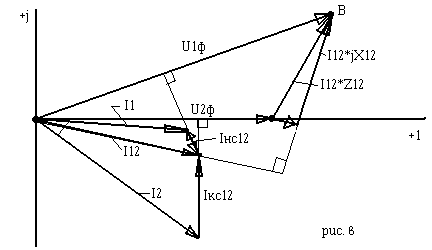
Вначале строим известные U2ф и I2.
Полагаем что U2ф=U2ф, т.е. напряжение U2ф направлено по действительной оси.
Емкостный ток 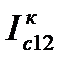 опережает на 90о напряжение U2ф. Ток I12 соединяет начало первого и конец второго суммируеммых векторов в правой части урав.(2) [I12=I2+
опережает на 90о напряжение U2ф. Ток I12 соединяет начало первого и конец второго суммируеммых векторов в правой части урав.(2) [I12=I2+ 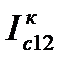 ]
]
Затем строим отдельно два слагаемых в правой части (3) [U1ф=U2ф+I12´Z12].
I12´Z12=I12´r12+I12´jx12 (7)
Вектор I12´r12 êê I12, вектор I12´jx12 опережает на 90о ток I12
Напряжение U1ф соединяет начало и конец суммируемых векторов U2ф, I12´r12, I12´jx12.
Ток 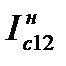 опережает U1ф на 90о.
опережает U1ф на 90о.
I1 соответствует (5) I1=I12+ 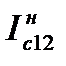
В линии с нагрузкой напряжение в конце линии по модулю меньше, чем в начале U2ф<U1ф.
5.4. Векторная диаграмма для расчета режима ЛЭП при заданном
токе нагрузки и напряжении в конце линии для линии в режиме
холостого хода
Вначале строим известные U2ф и I2.
Полагаем что U2ф=U2ф, т.е. напряжение U2ф направлено по действительной оси.
В линии на холостом ходу (I2=0), течет только емкостной ток, т.к. в соответствии с формулой I12=I2+Iкс12 (2) I12=Iкс12
Емкостный ток 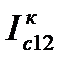 опережает на 90о напряжение U2ф.
опережает на 90о напряжение U2ф.
Затем строим отдельно два слагаемых в правой части (3) [U1ф=U2ф+I12´Z12], учитывая, что I12=Iкс12.
I12´Z12=I12´r12+I12´jx12 (7)
Вектор I12´r12 êê I12, вектор I12´jx12 опережает на 90о ток I12
Напряжение U1ф соединяет начало и конец суммируемых векторов U2ф, I12´r12, I12´jx12.
Ток 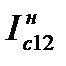 опережает U1ф на 90о.
опережает U1ф на 90о.
I1 соответствует (5) I1=I12+ 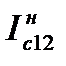
В этом случае напряжение в конце линии повышается U2ф>U1ф
Векторная диаграмма для такой линии:
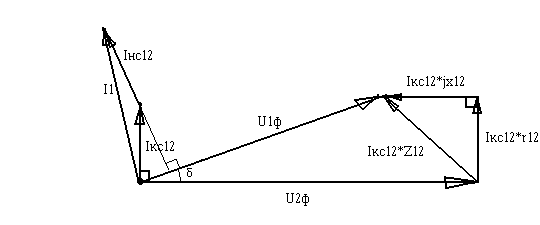
Задания для самостоятельной работы:
1. Расчет режима ЛЭП при заданном токе нагрузки и напряжении
в начале линии.
2. Анализ режимов ЛЭП в зависимости от соотношений параметров их схем замещения, режимов передачи активной и реактивной мощности, рабочих напряжений в начале и в конце линий.
Лекция 6. Падение и потеря напряжения в линии. Расчет режима ЛЭП при заданной мощности нагрузки и напряжении в конце и начале линии.
6.1. Падение и потеря напряжения в линии. Продольная и
поперечная составляющие падения напряжения
Различие в напряжениях U2ф и U1ф в П-образной схеме определяется падением напряжения на сопротивлении Z12 (Z12+jx12), вызванным током I12. Определяется это падением напряжения как сумма вектора I12r12, совпадающего по фазе с вектором I12 и вектора I12´jx12, опережающего вектор I12 на 90о.
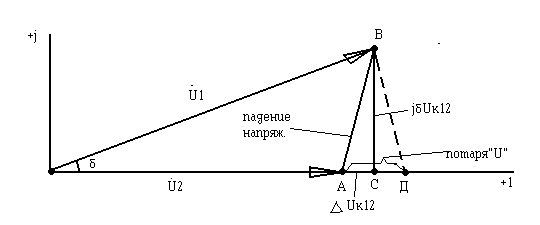
Падение напряжения – геометрическая (векторная) разность между комплексами напряжений начала и конца линий.
На рис. падение напряжения это вектор 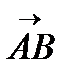 , т.е.
, т.е. 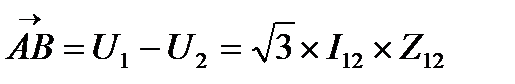
разность комплексных значений по концам линий, используется для характеристики режима линии.
Продольной составляющей падения напряжения DUк12 называют проекцию падения напряжения на действительную ось или на напряжение U2, DUк12=АС. Индекс “к” означает , что Uк12 – проекция на напряжение конца линии U2.
Обычно DUк12 выражается через данные в конце линии: U2, Pк12, Qк12.
Поперечная составляющая падения напряжения dUк12 – это проекция падения напряжения на мнимую ось, jdUк12=СВ. Т. о. U1-U2= 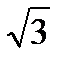 ´I12´Z12=DUк12+jdUк12.
´I12´Z12=DUк12+jdUк12.
Величина dUк12 определяет сдвиг вектора напряжения в начале линии (U1) на угол d по отношению к вектору напряжения в ее конце (U2).
Часто используют понятие потеря напряжения – это алгебраическая разность между модулями напряжений начала (U1) и конца (U2) линий.
На рис. çU1ê– êU2ê=АД.
Если поперечная составляющая dUк12 мала (например, в сетях Uном £ 110кВ), то можно приближенно считать, что потеря напряжения равна продольной составляющей падения напряжения.
Потеря напряжения является показателем изменения относительных условий работы потребителей в начале и в конце линии.
6.2. Расчет режима ЛЭП при заданной мощности нагрузки
и напряжении в конце линии
При подаче энергии по линии от начала к ее концу имеют место потери реактивной мощности. Они обусловлены реактивным сопротивлением линии и соответствующим ему реактивным сопротивлением схемы замещения этой линии. При передаче энергии имеют место и потери активной мощности, расходуемой на нагревание проводов. Поэтому в схеме замещения следует различать полную мощность до сопротивления Z12(r12+jx12), Sн12 и после него Sк12.
Задано напряжение в конце линии U2=сonst. Известна мощность нагрузки S2, напряжение U2, сопротивление и проводимость линии Z12=r12+jx12, в12.
| U1 |
| U2 |
| S1 |
| S2 |
- j 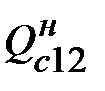
|
| r12 |
| x12 |
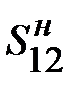
|
- j 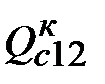
|
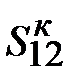
|
Необходимо определить напряжение U1, мощности в конце и в начале продольной части линии Sк12, Sн12, потери мощности DS12, мощность в начале линии S1. Для проверки ограничений по нагреву иногда определяют ток в линии I12.
Расчет аналогичен расчету при заданном токе нагрузке (I2), и состоит в последовательном определении от конца линии к началу неизвестных мощностей и напряжений при использовании I закона Кирхгофа и закона Ома. Будем использовать мощности трех фаз и линейные напряжения.
Зарядная (емкостная) мощность трех фаз в конце линии:
–jQкс12=3I*кс12´U2ф= 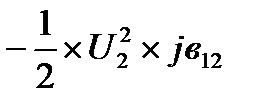
Мощность в конце продольной части линии по I закону Кирхгофа:
Sк12=S2 – jQкс12
Потери мощности в линии:
DS12=3I212Z12= 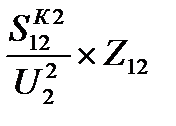
Ток в начале и в конце продольной ветви линии одинаков.
Мощность в начале продольной ветви линии больше, чем мощность в конце, на величину потерь мощности в линии, т.е. Sн12=Sк12+DS12
Линейное напряжение в начале линии по закону Ома равно:
U1=U2+ 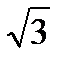 I12Z12=U2+
I12Z12=U2+ 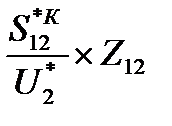
Емкостная мощность в начале линии:
-jQнc12= 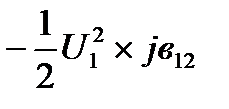
Мощность в начале линии:
S1=Sн12 – jQнс12
Под влиянием зарядной мощности Qс реактивная мощность нагрузки Q2 в конце, схема замещения уменьшается. Аналогичное явление имеет место и в начале схемы замещения, где реактивная мощность Qс уменьшает реактивную мощность в начале линии.
Это свидетельствует о том, что зарядная мощность сокращает реактивную мощность, поступающую от станции в линию для питания нагрузки. Поэтому зарядная мощность условно может рассматриваться как “генератор” реактивной мощности.
В линии электрической сети имеют место как потери, так и генерация реактивной мощности.
От соотношения потерь и генерации реактивной мощности зависит различие между реактивными мощностями в начале и конце линии.
6.3. Расчет режима ЛЭП при заданной мощности нагрузки
и напряжении в начале линии: использование нелинейного
уравнения узловых напряжений
Задано напряжение в начале линии.
Схема замещения:
| U1 |
| U2 |
| S1 |
| S2 |
- j 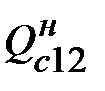
|
| r12 |
| x12 |
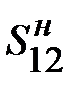
|
- j 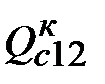
|
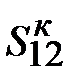
|
U1=сonst. Известны S2, U1 ,Z12=r12+jx12, в12.
Необходимо определить U2, Sк12, Sн12, DS12, S1
Т.к. U2 неизвестно, то невозможно определить последовательно от конца линии к началу определить неизвестные токи и напряжения по I закону Кирхгофа и закону Ома.
Нелинейное уравнение узловых напряжений для узла 2 имеет вид:
Y22U2+Y12U1=I2(U)=S*2/U*2
Это уравнение можно решить и найти неизвестное напряжение U2, а затем найти все мощности по выражениям:
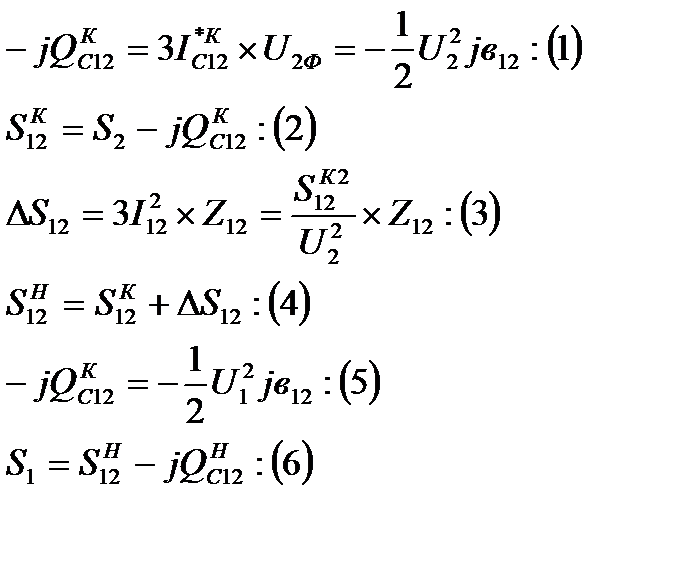
Но можно осуществить приближенный расчет в два этапа.
6.4. Расчет режима ЛЭП при заданной мощности нагрузки
и напряжении в начале линии: использование приближенного
расчета в два этапа
Задано напряжение в начале линии.
Схема замещения:
| U1 |
| U2 |
| S1 |
| S2 |
- j 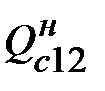
|
| r12 |
| x12 |
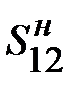
|
- j 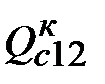
|
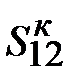
|
U1=сonst. Известны S2, U1 ,Z12=r12+jx12, в12.
Необходимо определить U2, Sк12, Sн12, DS12, S1
1 этап:
Предположим, что U2=Uном (7) и определим потоки и потери мощности аналогично выражениям (1)-(4), используя (7) получим:
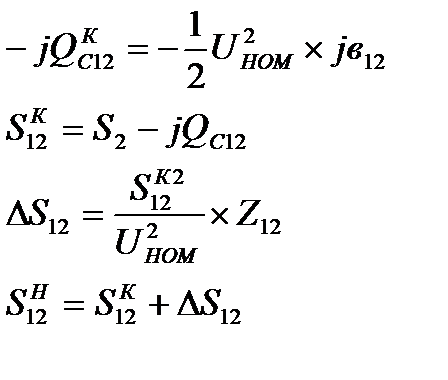
2 этап:
Определим напряжение U2 по закону Ома, используя поток мощности Sн12, найденный на 1 этапе. Для этого используем закон Ома в виде:
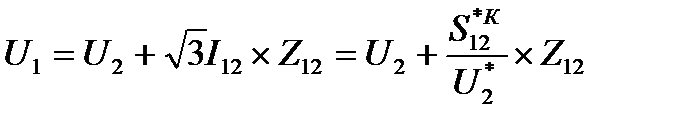 (7),
(7),
но выразим ток I12 через Sн12 и U1:
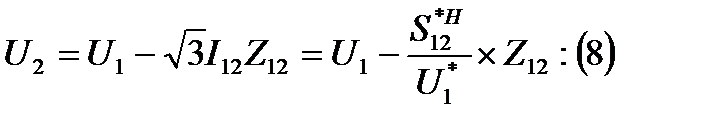
Потоки мощности на 1 этапе определены приближенно, поскольку в формулах вместо U2 использовали Uном.
Соответственно напряжение U2 на 2 этапе также определено приближенно, т.к. в последней формуле для U2 используется приближенное значение Sн12, определенное на 1 этапе.
Возможно итерационное повторение расчета, т.е. повторение 1-го и 2-го этапов для получения более точных значений мощности и напряжений. При проведении расчетов вручную, а не на ЭВМ, такое уточнение не требуется.
Задания для самостоятельной работы:
1. Составление расчетных схем сетей различной сложности.
2. Расчет к.п.д. электропередачи.
Лекция 7. Схема замещения и определение параметров двухобмоточного трансформатора и трансформатора с расщепленной обмоткой низшего напряжения.
На ПС применяют двух, трехобмоточные трансформаторы, а также АТ.
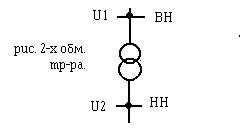
Двухобмоточный трансформатор условно обозначается так:
Первичная обмотка со вторичной имеет только магнитную связь.
Имеет две обмотки и связывает сети двух напряжений.
Трансформаторы выполняются либо трехфазными, либо однофазными (три однофазных трансформатора на ПС составляют одну трехфазную трансформаторную группу).
Дата добавления: 2015-09-14; просмотров: 3601;
