Предельная абсолютная и относительная погрешности.
Наилучшим критерием оценки точности измерений принято считать среднюю квадратическую погрешность (СКП) измерения, определяемую по формуле Гаусса:
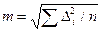
где Di=li-X (Х - истинное значение измеряемой величины, а li - результат измерения).
Так как, в большинстве случаях истинное значение неизвестно, то СКП определяют по формуле Бесселя:
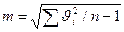
где Ji=li-х (х - средняя арифметическое значение или вероятнейшее значение измеряемой величины, а li - результат измерения).
СКП арифметической середины:
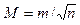
Эта формула показывает, что СКП арифметической середины в Ön раз меньше СКП отдельного измерения.
На практике различают предельные и относительные погрешности. Теорией доказывается, а практикой подтверждается, что абсолютное большинство случайных погрешностей находится в интервале от 0 до m - 68% , от 0 до 2m - 95% , от 0 до 3m - 99.7%.
На практике за предельную погрешность принимают 2m, т.е. с вероятностью 95% можно утверждать, что случайные погрешности не превысят величины равной 2m. Если n<10 то Ji(пред)=tB . M, где tB - коэффициент Стьюдента (таблица)
Таблица коэффициентов Стьюдента
| n | tB | n | tB | n | tB |
| 4,53 | 2,65 | 2,37 | |||
| 3,31 | 2,52 | 2,32 | |||
| 2,87 | 2,43 | 2,28 |
Рассмотрим на примере как выполняется математическая обработка результатов ряда равноточных измерений. Пусть длина линии измерена шесть раз (см. таблицу). Необходимо найти вероятнейшее значение измеренной величины и оценить результаты измерений.
| N | l,м | E,см | J,см | J2 | Вычисления |
| 75.15 | +5 | -1 | l'=75.10 м, x =75.10+0.37/6=75.16 м, m =Ö91 / 5=4.2 см, М = 4.2 / Ö6=1.7 см, Ji(пред)=tB . M = 2.52 . 1.7 = 4.4 см, L = 75.16 + 0.04 м (P=95%), Отн.погр.DL/L=4.4/7510=1/1700 | ||
| 75.18 | +8 | +2 | |||
| 75.20 | +10 | +4 | |||
| 75.13 | +3 | -3 | |||
| 75.10 | -6 | ||||
| 75.21 | +11 | +5 | |||
| S | +1 |
Матобработка ряда измерений одной и той же величины выполняется в следующей последовательности:
- определение вероятнейшего значения измеренной величины x=Sli/n;
- оценка точности отдельного измерения 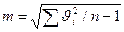
- оценка точности арифметической середины (вероятнейшего значения) 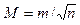
- определение окончательного результата L = x ± tBM.
Дата добавления: 2015-09-14; просмотров: 1043;
