Спонтанный экономический порядок и идеальные типы государства

Происхождение государства: экономическая теория анархии.Важно заметить, что из наличия у государства сравнительных преимуществ в эффективности производства общественных благ так или иначе связанных со спецификацией и защитой прав собственности не следует непосредственно необходимость его возникновения: далеко не каждый эффективный общественный институт оказывается жизнеспособным институтом. Для того, чтобы объяснить процесс генезиса государственной власти необходимо обратиться в первую очередь к целевым функциям индивидов, составляющих основу этой власти.

Вопрос о происхождении государства интересовал множество людей еще до появления экономической науки как таковой. Определенный прорыв в объяснении причин и механизмов возникновения государственной власти был достигнут философией Нового Времени.

Этот прорыв связывают, в первую очередь, с именами английских философов Томаса Гоббса и Джона Локка и француза Жана-Жака Руссо. Каждый из них принимал за точку отсчета общественного развития некое «естественное состояние» общества — состояние, которое многие современные исследователи называют «анархией». Вообще говоря, каждый из этих философов понимал под категорией «естественное состояние» нечто свое, причем понимания Гоббса и Руссо достаточно близки друг к другу (хотя оценивается это естественное состояние ими диаметрально противоположно) и сильно отличаются от понимания естественного состояния общества Джоном Локком.

«Естественное состояние» по Гоббсу и Руссо предполагает фактически полное отсутствие какого-либо положительного сотрудничества между находящимися в нем индивидами, поэтому права собственности и все остальные атрибуты цивилизации отсутствуют как таковые. Однако, как убедительно показали многочисленные антропологические исследования и исследования биологов, занимающихся изучением поведения приматов, в такого рода «естественном состоянии» никогда не находились (да и не могли находиться) не то что люди, а даже высшие приматы.

Нет никаких сомнений в том, что предок у людей и у человекообразных обезьян (горилл и шимпанзе) один и тот же. Из общих особенностей социального поведения людей и человекообразных обезьян мы можем сделать заключение о го-мологичности их поведения, обусловленности его существованием одного и того же предка и у тех, и у других. Шимпанзе, так же как и люди, живут группами, их поведение регулируется с помощью внутригрупповых правил, в этих группах существует устойчивая иерархическая система. Более того, исследователи обнаружили у шимпанзе зачатки частной собственности и даже нечто, очень напоминающее человеческие войны. Таким образом, по словам П. Рубина: «Никогда не было такого времени, когда люди жили бы без общественных правил. По мере того, как наши предки развивались и становились более разумными, правила усложнялись, но состояния, в котором люди жили бы без правил не может быть

определено. «Естественное состояние», в таком случае, описывается правилами, существовавшими на тот момент, когда люди стали людьми»93.

Таким образом, «естественное состояние» в понимании Руссо и Гоббса представляет собой химеру, никогда не существовавшую в действительности. В современном понимании, анархическое состояние общества — это система, в которой участники захватывают чужие ресурсы и защищают свои при отсутствии регулирования этого процесса сверху. Анархия — «это не хаос, а скорее спонтанный порядок»94. Такое понимание анархии достаточно близко к пониманию «естественного состояния» общества Джоном Локком: в «естественном состоянии» по Локку присутствуют такие институты, как церковь, семья, собственность и т. д., нет только института государственной власти. Иными словами, Хиршлейфер и другие современные исследователи, вслед за Локком, рассматривают анархию, как феномен, описывающий взаимодействие не обособленных индивидов, а их групп, абстрагируясь от механизмов взаимодействия индивидов внутри этих групп. При таком подходе с помощью категории анархического взаимодействия могут быть описаны не только взаимоотношения первобытных племен, но и, например, международная борьба за контроль над мировыми ресурсами, ведущаяся на уровне независимых государств или любая война между независимыми государствами.

В истории экономики существует множество примеров более или менее длительного существования сообществ без центральной власти. Существует масса исследований, объясняющих причины устойчивого существования таких сообществ. В частности, по мнению Глакмана, исследовавшего жизнь народа ну-эров, главными среди этих причин являются наличие в таких сообществах институтов возмездия за нанесенный ущерб, поддерживаемых специальными группами возмездия: именно таким образом, в частности, до сих пор поддерживается существующий даже в некоторых европейских сообществах институт вендетты, предполагающий, что все кровные родственники несут коллективную ответственность за каждого члена группы95. Другим важнейшим институтом, поддерживающим равновесие в безгосударственных сообществах, Глакман называет институт компенсации: механизм избежания возмездия с помощью значительной материальной компенсации. Оба этих института выступают в роли средств сдерживания потенциального нарушителя, снижая, таким образом, издержки обеспечения прав собственности.

Ричард Познер сосредоточивает свое внимание на роли, которую играет в безгосударственных сообществах институт взаимного страхования от голода96. Отсутствие развитой технологи общественного производства, низкий уровень развития научно-технических знаний, ограниченный ассортимент производимой в таких сообществах продукции, отсутствие внешней торговли, слабое развитие техники делают риск неурожая в первобытных земледельческих сообществах колоссальным. Поэтому главным экономическим мотивом индивидов в таком сообществе становится не максимизация индивидуального дохода, а выжива-

93Rubin, Paul H. (1998), The State of Nature and the Evolution of Political Preferences, Department ofEconomics Emory University Working Paper Series, 4.

94Hirshleifer, Jack (1995), Anarchy and its Breakdown, 103Journal of Political Economy, 26.

95Gluckman, Max (1956), Custom and Conflict in Africa, Oxford: Basil Blackwell.

96Posner, Richard A. (1980), A Theory of Primitive Society, with Special Reference to Law, 23 Journal of Law and Economics, 1-53.

ние, которое легче обеспечить не по одиночке, а всей группой. Поэтому в таких группах и возникают институты взаимного страхования, включающие в себя распределение внутри группы излишков урожая, приношение даров, брачные и родственные правила и другие институты, способствовавшие относительному выравниванию богатства у всех членов сообщества.

Наконец, Амбек, исследовавший в своих работах механизмы формирования и поддержания прав собственности во время калифорнийской «золотой лихорадки»97, выделил в качестве еще одного необходимого условия жизнеспособности безгосударственного сообщества относительно равномерное распределение потенциала насилия в таком сообществе. Независимые старатели в модели Амбека распределяют свои усилия между добычей золота на своем участке и насилием, которое принимает форму вытеснения других лиц с участка земли. Отдача от усилий и в том, и в другом случае сокращается, поэтому каждый старатель будет стремиться к равенству предельных продуктов усилий обоих типов. Иначе говоря, индивид, обладающий сравнительными преимуществами в осуществлении насилия будет, при прочих равных условиях, обладать участком большим, по сравнению с другими старателями, участком земли. Если снять предпосылку об относительно равномерном распределении потенциала насилия, увеличивается вероятность появления такого индивида или группы, который найдет для себя выгодным захватить все имеющиеся участки. Если, далее, мы предположим, что потенциал насилия, при прочих равных условиях, распределяется пропорционально богатству членов общества, то выводы Амбека и Познера тесно связаны друг с другом.

На сегодняшний день спонтанный экономический порядок сохранился только в наименее развитых обществах (да и то, лишь отчасти). Поэтому вопрос о том, почему такой порядок оказывается нежизнеспособен в долгосрочном аспекте представляется более интересным, чем вопрос о механизмах самоподдержания такого порядка. Для того, чтобы ответить на этот вопрос обратимся к теории анархии, предложенной Джеком Хиршлейфером.

Первоначально в его модели действуют всего два индивида или группы, распределяющие имеющиеся у них ресурсы между производством благ и насилием, целью которого является не только захват чужих ресурсов, но и защита собственных (захват чужих потребительских благ и защита своих в модели не рассматривается):

Ri=aiEi+biFi

Где i = 1,2; Е; — производственные усилия i-того индивида, F; — его военные усилия; а, и bj — издержки конверсии единицы ресурсов в производственные и военные усилия соответственно.

Интенсивность производственных и военных усилий i-того индивида определяется как:

Соответственно:

Далее, Хиршлейфер рассматривает доход, получаемый каждым из индивидов как степенную функцию от используемых ресурсов:

97 См.: Umbeck, John R. (1978), A Theory of Contractual Choice and the California Gold Rush, 2 Journal of Law and Economics, 421–437; Umbeck, John R. (1981), A Theory of Property Rights with Applications to the California Gold Rush, Ames: Iowa State University Press.

Доля ресурсов, которую контролирует каждый из индивидов определяется эффективностью военных усилий и равняется р; (pi + р2 = 1; Rj = PiR). Технология конфликта отражается функцией успеха в соперничестве (Contest Success Function — CSF), которая определяет пропорцию успеха (pi/рг) как функцию относительных военных усилий (F^):

Рг (А)

Здесь m — ключевой для дальнейшего анализа «параметр решительности», отражающий эффективность наступательных военных усилий, относительно эффективности оборонительных усилий, m > 0.

Из предыдущего уравнения можно получить доли ресурсов, контролируемых каждым из индивидов, как функциональные зависимости от Fi и F2:

р"

р""

1 2

На рис. 5.1 отражена взаимосвязь между долей ресурсов, которую контролирует 1-й индивид и его военными усилиями при фиксированных военных усилиях второго индивида и различных т.

Здесь на горизонтальной оси отражены военные усилия Fb а на вертикальной — доля ресурсов, контролируемых первым индивидом (р]).

Стоит заметить, что вообще говоря, термин «военные усилия» условен. Этот показатель может быть применен, например, к ситуации соперничества политических партий за власть в современной демократической стране. Поэтому и действие «параметра решительности» отнюдь не ограничивается ситуацией вооруженного противоборства двух индивидов или групп. Так, например, в современных демократиях такие институты, как права человека и разделение властей сокращают этот параметр.

Рисунок 5.1. Функция успеха в соперничестве9*

1 0,9-

+ F2 = 25

0,7-

0.6-

m = 0,5

05-

I

0.4-

f …

m = 1

0.3-

,-\

0,2-

0.1-

C 35 40 46

98 Hirshleifer, Jack (1995), Anarchy and its Breakdown, 103 Journal of Political Economy, 32.

Из предшествующих выкладок получаем:

F2R2)m

И, наконец, приходим к условиям равновесия между выбираемыми сторонами уровнями интенсивности военных усилий и долями ресурсов, которые контролирует каждая из сторон:

Гт п

Т I

J2 К2

[()

h)

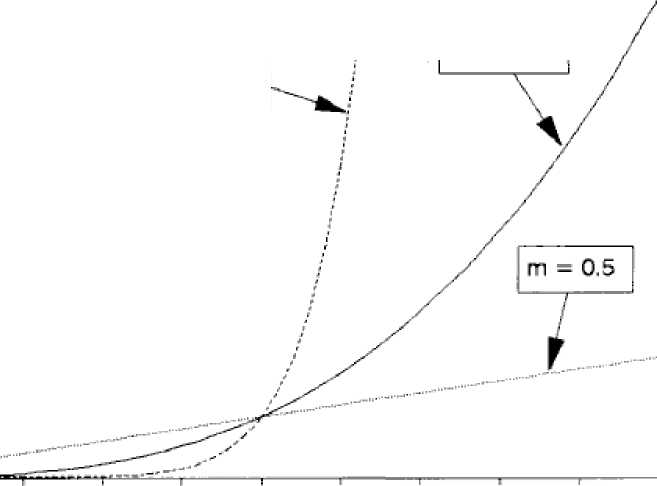
Из последнего уравнения следует, что при стремлении m к единице, pi/p2 —> 0, если fi > f2, и pi/p2—> оо, если fi< f2 (см. рис. 5.2).

На этом рисунке по горизонтальной оси отложена относительная интенсивность военных усилий (fi/f2), а по вертикальной — пропорция успеха (pi/p2).

Из всего предшествующего изложения вытекает первое условие, при соблюдении которого анархическая система будет относительно устойчивой, а именно, для динамической стабильности системы необходимо, чтобы «параметр решительности» был меньше 1. Проиллюстрируем это числовым примером. Положим R = 100, f\ = 0,1, f2 = 0,2, m = 2/3. Тогда:

/(l-m)

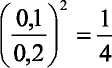
.99

Ri = 20, R2 = 80. Рисунок 5.2. Интенсивность военных усилий и пропорция успеха

m = 0.75

m = 0.9

в

7 6–5 4

1-

0–2 0.4 0.6 0.6

1.2 1.4 1.6 1.8

Если первоначальное распределение ресурсов иное, то каждое последующее взаимодействие между противоборствующими сторонами будет асимптотически приближать распределение ресурсов к равновесному уровню. Например, в рассмотренном примере, при сохранении всех остальных параметров, если первоначально ресурсы распределены в пропорции 3/2 (Ri° = 60, R2 = 40), то конфликтное взаимодействие между сторонами в первом периоде приведет к

Ibid., 34.

новому распределению ресурсов: R/ = 45,2, R2' = 54,8. Продолжение конфликта во втором периоде установит новые параметры распределения ресурсов: R]2 = 35,7, R22 = 64,3. И так далее.

Если же параметр m > 1, например, m = 2, распределение ресурсов не будет стремиться к равновесному состоянию. Так, в рассматриваемом примере, при Ri° = 60, R20 = 40 и m = 2, Ri1 = 36, R21 = 64; Ri2 = 7,3, R22 = 92,7, и так далее. То есть, система удаляется от равновесия с каждым следующим взаимодействием.

Другим необходимым условием стабильности анархической системы будет, естественно, наличие у каждой из соперничающих сторон в динамическом равновесии по меньшей мере минимального уровня доходов, у, обеспечивающего выживание каждого из конкурентов (Yj > у, i=l,2).

Заметим также, что эти два условия являются не достаточными, но только необходимыми условиями устойчивости анархической системы.

Далее, предположим, что каждая из конкурирующих сторон пытается максимизировать свой собственный доход, выбирая оптимальную интенсивность своих военных усилий и полагая заданной интенсивность усилий конкурента. Очевидно, что в этом случае мы имеем дело с классической дуополией Курно. Целевые функции соперничающих индивидов или групп будут выглядеть как:

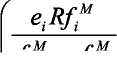
fl\Ji +/2

Где i = 1,2; aiei + Ъ& = 1; М = m/(l-m).

Решая это уравнение для каждого из соперников, получаем соответствующие кривые реакции (RQ и RC2):

f" — м

М

Если же принять достаточно реалистичную для условий анархии предпосылку, что и производственные и военные технологии обоих субъектов одинаково эффективны, мы получим условие равновесия при симметричном двустороннем конфликте:

Мт

Как показывает это уравнение, интенсивность военных усилий сторон при симметричном конфликте обратно пропорциональна издержкам конверсии единицы ресурсов в военные усилия, и прямо пропорциональна «параметру решительности», отражающему эффективность наступательных военных усилий, относительно эффективности оборонительных усилий.

Симметричное решение при b = 1 отражено на рис. 5.3.

Здесь по горизонтальной оси отложена интенсивность военных усилий первого индивида или группы, а по вертикальной — второго индивида или группы. Как видно на этом графике, равновесный объем военных усилий увеличивается с ростом т.

Так как, при симметричном конфликте pi = р2 = 1/2, максимальный для каждой из сторон доход будет представлен следующим уравнением:

Иначе говоря, доход каждой из сторон растет с увеличением совокупного объема доступных ресурсов R и ростом параметра производительности h; и падает с ростом «параметра решительности» m и издержек конверсии единицы ресурсов в производственные усилия а.

Следующим шагом будет увеличение числа индивидов или групп, действующих в анархической системе до N. В этом случае целевая функция первого из этих конкурентов будет выглядеть как:

Соответственно, кривая реакции первого конкурента RQ:

/i

м

М

М

/2

= 2/Зш

Рисунок 5.3. Кривые реакции для т = 1/2 ит = 2/З