Индивидов

При этом, необходимым условием является то, что объем расходов на производство общественных благ G (при условии, что цена единицы общественного блага равна 1) не должен превышать доходов, получаемых оседлым бандитом от налогообложения (G < tr(t)Y(G)). Обратим также внимание на то обстоятельство, что доход автократа от налогообложения зависит от G, в то время как оптимальный уровень ставки налога (t) от этого параметра не зависит.

Решая задачу максимизации чистого дохода оседлого бандита по t, мы получим следующее уравнение:

Так как Y(G) > 0, условие максимизации чистого дохода оседлого бандита по ставке налогообложения приводится к виду:

Отсюда, оптимальная ставка налога t:

И, соответственно, максимальная доля потенциального дохода Y, достающаяся автократу:

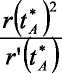
Иначе говоря, максимизация этой доли достигается в том случае, когда предельное сокращение доходов автократа от увеличения потерь от мертвого груза (tr'(t)dt) равно предельному увеличению его доходов от роста ставки налога (rdt).

Параметр, обратный оптимальной ставке налогообложения — это показатель самоограничения или реципрокности оседлого бандита:

104 McGuire, Martin С. and Olson, Mancur Jr. (1996), The Economics of Autocracy and Majority Rule: The Invisible Hand and the Use of Force, 34 Journal of Economic Literature,72–96.

Максимизация функции чистого дохода автократа по расходам на производство общественных благ при оптимальной ставке налогообложения достигается при условии:

Или:

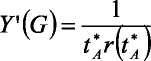
Так как, по определению, rY = I, предельное изменение реальных общественных доходов I по уровню расходов оседлого бандита на производство общественных благ G равно показателю его реципрокности:

Иными словами, автократ будет увеличивать производство общественных благ до тех пор, пока предельный прирост реальных доходов общества от увеличения количества предоставляемых общественных благ не станет равно показателю самоограничения оседлого бандита.

Вводя в модель новые зависимые переменные Q и Р, Олсон и МакГир получают возможность представить все условия равновесия в модели оседлого бандита на одном графике:

Установление равновесной ставки налогообложения подданных оседлого бандита и равновесного объема предоставляемых им общественных благ позволяют определить как равновесный реальный доход общества, так и распределение этого дохода между автократом и его подданными (см. рис. 5.5).

Во втором квадранте рис. 5.5 отражен выбор автократом оптимальной ставки налогообложения (tA*), при которой максимизируется доля потенциального дохода Y, достающаяся ему

TA*r).

Пересечение кривых, отражающих уровень самоограничения оседлого бандита (1/tr и 1/t) с кривыми Q(tA*) и P(tA*) определяют оптимальный предельный прирост, соответственно, потенциального и реального доходов общества по количеству производимых автократом общественных благ. Определяемое таким образом оптимальное количество последних вместе с функциями rA*Y(G) и tA* (G) показывает в квадранте IV распределение реальных доходов общества между автократом (отрезок АВ), его подданными (отрезок ВС) и расходами на поддержание порядка (отрезок ОА).

Важно заметить, что хотя каждой оптимальной ставке налогообложения соответствует определенное количество предоставляемых оседлым бандитом общественных благ, выбор из всех возможных ставок налогообложения оптимальной от G не зависит, поэтому автократ сначала определяет оптимальное t, а уже потом, на основании этого t определяет оптимальную для себя величину расходов на общественные блага.

Из модели Олсона — МакГира можно сделать вывод, что оседлый бандит всегда будет стремиться обеспечить некий оптимальный уровень спецификации и защиты прав собственности для своих подданных, однако, история знает достаточно обратных примеров. В частности, в качестве одного из таких примеров можно привести деятельность английской династии Стюартов. С того момента, когда в 1603-го году им досталась Корона, и до Славной Революции Стюарты обладали фактически неограниченной властью, однако, несмотря на стимулы к увеличению ожидаемых доходов казны, Корона преследовала краткосрочные цели, нарушая, при этом, данные обязательства. Среди основных источников

пополнения королевской казны были слабо согласующаяся с долгосрочными интересами Стюартов продажа королевских земель, вызывавшая возмущение наследственной аристократии торговля новыми дворянскими титулами, подрывавшая основы конкуренции продажа монопольных прав, введение новых налогов и практика заимствований, которые Стюарты далеко не всегда возвращали. Все это, в конечном итоге и привело к революции.

Рисунок 5.5. Равновесие в модели оседлого бандита

Ibid., 79.

Возникает естественный вопрос: почему автократы далеко не всегда ведут себя так, как они должны себя вести в соответствии с логикой модели Олсона — МакГира? Существует как минимум три возможных варианта ответа на этот вопрос. Во-первых, монарх может быть настолько оторван от реальной действительности, что он может просто не обладать информацией, необходимой для выбора оптимальной стратегии. Во-вторых, автократ может действовать в такой институциональной среде, которая не способствует сколько-нибудь удовлетворительной спецификации и защите прав собственности, и автократ не в состоянии эти правила изменить. Наконец, третий аргумент, на котором, в частности, акцентирует свое внимание Мансур Олсон106, заключается в том, что автократ может по каким-то причинам не интересоваться будущим. Именно в силу этой последней причины, по мнению Олсона, многие современные диктаторы в странах третьего мира склонны к грабительской внутренней политике.

«В таких обстоятельствах для общества может оказаться выгодным достижение согласия по вопросу о том, кто будет следующим руководителем государства, так как это снижает издержки, возникающие из-за отсутствия при автократическом режиме независимой силы, которая могла бы установить мирную преемственность государственной власти»107.

Таким образом, Олсон выдвигает серьезный экономический аргумент в оправдание монархических династий.

Контрактная модель государства.Если в предыдущем разделе речь 1^^ шла об абсолютно вертикальном социальном контракте, то здесь мы ос-*- ^-тановимся на его полной противоположности — контракте совершенно горизонтальном. Строго говоря, и то и другое — суть абстракции: совершенно вертикальный, равно как и совершенно горизонтальный социальные контракты невозможны. Однако, если модель оседлого бандита во многих случаях оказывается полезной для анализа автократической власти, то модель консенсусной демократии, которой посвящен этот раздел, полезна для анализа современного демократического общественного устройства. Рассматриваемая здесь модель консенсусной демократии, так же как и рассмотренная в предыдущем разделе модель оседлого бандита, была предложена Мансуром Олсоном и Мартином МакГиром108.

Для общества консенсусной демократии характерны следующие условия: во-первых, все средства, которые общество собирает в виде налогов идут на производство общественных благ; во-вторых, достающееся каждому индивиду количество общественных благ прямо пропорционально его вкладу в производство этих благ, иными словами, отсутствует какое-либо перераспределение доходов.

Прежде всего необходимо заметить, что в отличие от автократа, для которого выбор оптимальной ставки налогообложения не зависит от объема предоставляемых им общественных благ G, при консенсусной демократии параметры G и t связаны между собой обоюдной связью. Поэтому вместо двух задач, которые последовательно решает оседлый бандит (выбор оптимальной ставки налогообложения t* и затем уже на этой основе выбор оптимального количества

106Olson, Mancur Jr. (1993), Dictatorship, Democracy, and Development, 87 American Political Science Review, 567–576.

107Ibid., 572.

108McGuire, Martin С and Olson, Mancur Jr. (1996), The Economics of Autocracy and Majority Rule: The Invisible Hand and the Use of Force, 34 Journal of Economic Literature, 80–83.

общественных благ G*), общество в условиях консенсусной демократии должно решить одну, но более сложную задачу, которая отражена в следующей системе уравнений:

W = max(l — t)r{t)Y(G) U = max([r(f[G])7(G)]- G)

G

G

Решение первого из этих уравнений приводит к нахождению оптимальной ставки налогообложения в демократическом обществе, решение второго позволяет определить оптимальное количество производимых общественных благ. При этом, так как все собранные налоги тратятся без остатка на производство общественных благ, необходимо выполнение следующего условия:

tr(t)Y(G)-G = O Решая второе из уравнений представленной системы, получим:

rT{G)+Yr}{t)— -1 = 0 W K'dG

Здесь rY'(G) — предельные выгоды общества от увеличения количества производимых общественных благ на единицу, Yr'(t)<5t/<5G — предельные издержки связанные с этим увеличением, вызванные ростом потерь от мертвого груза, 1 — себестоимость производства единицы общественных благ.

Далее, решая первое из уравнений системы получаем:

Отсюда:

dG_Y(

dt 1-trY1trT-l

Подставляя полученное таким образом значение <5G/<5t в решение второго уравнения нашей системы получим:

r{t)T{G) — фУ(0 f ^'(G)~! 4i-1 = 0 W V; W K;Y(Glr(t)+tr'(t)]

Отсюда:

r{t)

Значения переменной t, являющееся решением данного уравнения и будет оптимальной ствкой налогообложения в условиях консенсусной демократии tN*, соответственно, r(tN*) = rN*.

Так как r(tN*)Y'(G) = I'(tN*, G), умножив обе части предыдущего уравнения на rN*, мы получим условие оптимального производства общественных благ в обществе без перераспределения:

Здесь MSCN* — общественные издержки предоставления одной дополнительной единицы общественных благ при оптимальной ставке налога tN*. Выражение {-[(l-t*)(r*)7r*]} — это предельные потери мертвого груза при оптимальной ставке налогообложения, а 1 — издержки производства единицы общественных благ G. Так как r'(t*) < 0, MSCn* > 1, то есть увеличение производства общественных благ на единицу обойдется обществу дороже себестоимости единицы общественных благ, так как для финансирования дополнительного производства общественных благ необходимо увеличить ставку налога t, а это приведет к увеличению издержек мертвого груза.

Графическая иллюстрация равновесных параметров общества консенсусной демократии приводится на рис. 5.6. Здесь во втором квадранте представлены оптимальная ставка налогообложения tN* и соответствующие ей оптимальные показатели предельных издержек предоставления общественных благ для реального (MSC) и оптимального (V) общественного дохода. В первом квадранте рис. 6 определяется оптимальное, для условий консенсусной демократии, коли-

чество общественных благ GN*. В четвертом квадранте рис. 6 отражен оптимальный, для общества без перераспределения доходов, объем налоговых поступлений (tN*IN = GN*).

Рисунок 5.6. Равновесие в модели консенсусной демократии

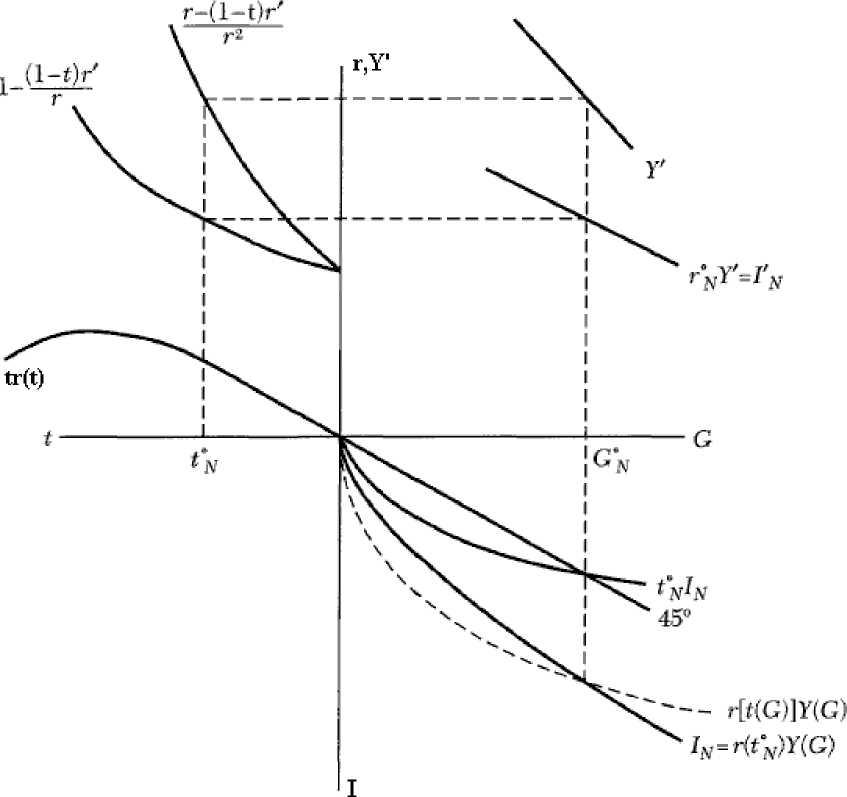
Обратим внимание на то обстоятельство, что из представленных в этом и предыдущем разделах моделей невозможно сделать однозначный вывод о том, в каком из рассмотренных обществ равновесный объем производства общественных благ будет, при прочих равных условиях, выше. Для того, чтобы попытаться ответить на этот вопрос, обратимся к простой модели, предложенной Финдли и Уилсоном110. В этой модели объем собираемых в обществе налогов (Т) прямо пропорционален произведенному в экономике доходу Y. Последний является функцией от затрат труда на поддержание порядка (Y = Y(Lg)), причем, так как отдача от затрат труда на поддержание порядка сокращается по мере увеличения этих затрат, функция Y(Lg) не монотонная и при определенном Lg = Lg*, достигает максимума. Расходы на поддержание порядка (G) — это возрастающая убывающим темпом функция от затрат труда на поддержание порядка (G = G(Lg), <5G/<5Lg > 0, c^G/SLg2 < 0). Условия максимизации чистого дохода в автократической системе и в обществе консенсусной демократии представлены на рис. 5.7. Целью автократа являет-

109Ibid., 32.

110Findlay, Ronald and Wilson, John D. (1984), The Political Economy of the Leviathan, Institute forInternational Studies, Stockholm, Seminar Paper No.285; см. также: Эггертссон Т. (2001), Экономическое поведение и институты, М: Дело, с. 341–349.

ся максимизация ренты, определяемой как разность между налоговыми поступлениями и расходами на поддержание порядка (R(Lg) = T(Lg) — G(Lg)), поэтому, для получения максимальной ренты R(LA*), автократ будет обеспечивать порядок в обществе, на уровне, соответствующем

*),а

затратам труда Ьд*. Тогда общий объем налоговых поступлений автократа составит t$L произведенный в автократическом государстве совокупный доход будет равен Y(La*).

Рисунок 5.7. Оптимальные расходы на поддержание порядка и