Вращение вокруг проецирующих прямых
Рассмотрим, как изменится положение точки А при её вращение вокруг оси i на некоторый угол j (рис. 5.5).
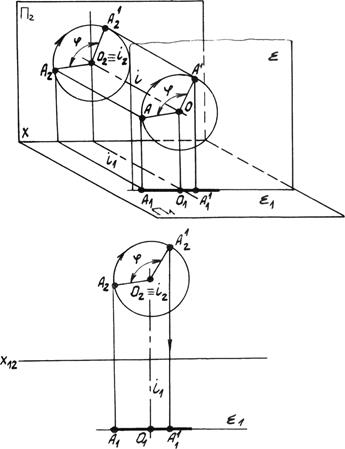
Рис. 5.5. Вращение точки.
Ось i перпендикулярна плоскости проекций p2 (фронтально проецирующая прямая). При вращение точка А будет перемещаться по окружности, плоскость которой å параллельна плоскости проекций p2. На плоскость p2 окружность спроецируется без искажения, а на плоскость p1 - в виде прямой å1, параллельной оси x12. Радиус окружности равен расстоянию от точки до оси. Для поворота точки А на некоторый угол j на фронтальной проекции перемещаем А2 по окружности на угол j. Определяем новое положение точки А 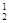 . Горизонтальная проекция точки А1 перемещается по траектории параллельной оси x12. Новую горизонтальную проекцию А
. Горизонтальная проекция точки А1 перемещается по траектории параллельной оси x12. Новую горизонтальную проекцию А 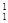 определяем по линии связи от А
определяем по линии связи от А 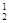 . Аналогично, при вращение точки вокруг оси, перпендикулярной плоскости p1, горизонтальная проекция точки будет перемещаться по окружности, а фронтальная – по прямой линии параллельной оси x12.
. Аналогично, при вращение точки вокруг оси, перпендикулярной плоскости p1, горизонтальная проекция точки будет перемещаться по окружности, а фронтальная – по прямой линии параллельной оси x12.
Задача: Определить натуральную величину отрезка АВ прямой общего положения. Преобразовать данную прямую в проецирующую (рис. 5.6).
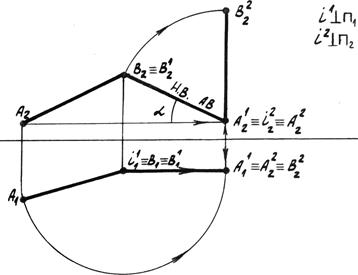
Рис. 5.6. Вращение прямой.
Решение: Чтобы определить натуральную величину отрезка прямой общего положения, необходимо преобразовать его в прямую уровня. Одна из проекций прямой уровня параллельна оси x12. Выбираем ось вращения i1 перпендикулярно плоскости p1. Чтобы повернуть прямую линию на некоторый угол j, необходимо повернуть на этот угол две её точки. Но задачу можно упростить, если ось вращения будет совпадать с одной из точек прямой. В нашем случае ось совпадает с точкой В. Эта точка остаётся неподвижной. Остаётся повернуть точку А до положения, когда отрезок АВ окажется параллельным плоскости p2. Проекция А 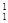 В
В 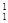 || x12, на фронтальной проекции точка А2 перемещается параллельно оси x12. Данная прямая линия преобразована таким вращением во фронталь. Проекция А
|| x12, на фронтальной проекции точка А2 перемещается параллельно оси x12. Данная прямая линия преобразована таким вращением во фронталь. Проекция А 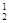 В
В 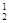 является натуральной величиной отрезка АВ, а угол a - угол наклона к прямой плоскости p1.
является натуральной величиной отрезка АВ, а угол a - угол наклона к прямой плоскости p1.
Вторым вращением преобразуем отрезок АВ в проецирующую прямую. Для этого ось вращения с2 выбираем перпендикулярно плоскости p2. Ось i2 совпадает с точкой А, которая останется неподвижной при втором вращении. Повернём точку В до положения, когда прямая займёт положение перпендикулярно плоскости проекций p1. На фронтальной проекции - А 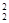 В
В 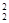 перпендикулярна оси x12, а на горизонтальной – проекции - В
перпендикулярна оси x12, а на горизонтальной – проекции - В 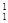 перемещается параллельно оси x12 и совпадает с проекцией А
перемещается параллельно оси x12 и совпадает с проекцией А 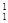 . Новая горизонтальная проекция прямой А
. Новая горизонтальная проекция прямой А 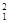 В
В 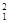 преобразуется в точку. Вторым вращением данная прямая преобразована в горизонтально проецирующую.
преобразуется в точку. Вторым вращением данная прямая преобразована в горизонтально проецирующую.
Задача: Преобразовать плоскость Т общего положения во фронтально проецирующую. Определить угол её наклона к плоскости p1 (рис. 5.7).
Решение: Чтобы повернуть плоскость вокруг какой - либо оси на угол j, необходимо повернуть на этот угол геометрические элементы, определяющие плоскость на чертеже.
Для преобразования плоскости Т во фронтально проецирующую необходимо повернуть её на такой угол, чтобы горизонтальный след плоскости оказался перпендикулярным оси x12. Выбираем ось вращения i перпендикулярно плоскости p1 так, чтобы в пределах чертежа определялась неподвижная точка плоскости Т - точка пересечения оси i с плоскостью Т. Эту точку
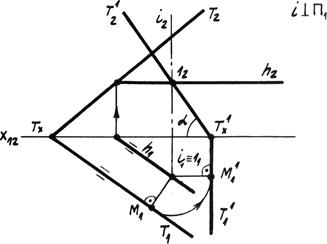
Рис. 5.7. Вращение плоскости.
1 (11,12) определяем с помощью горизонтали плоскости h. Определяем радиус вращения горизонтального следа плоскости Т – i1M1 ^ T1. Поворачиваем след плоскости Т1 перпендикулярно оси x12, радиус вращения i1 M 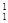 || x12. Определяется новая точка схода следов плоскости Т
|| x12. Определяется новая точка схода следов плоскости Т 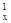 . Для определения нового фронтального следа Т
. Для определения нового фронтального следа Т 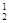 соединяем точку схода следов Т
соединяем точку схода следов Т 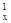 с фронтальной проекцией неподвижной точки плоскости 12. Плоскость Т преобразована во фротально проецирующую, угол a - угол наклона плоскости Т к плоскости проекций p1.
с фронтальной проекцией неподвижной точки плоскости 12. Плоскость Т преобразована во фротально проецирующую, угол a - угол наклона плоскости Т к плоскости проекций p1.
Задача: Определить натуральную величину треугольника АВС способом вращения (рис. 5.8).
Решение: Первым вращением вокруг оси i, перпендикулярной плоскости p2 и совпадающей с точкой В, преобразуем треугольник АВС в горизонтально проецирующую плоскость. Провернём фронтальную проекцию треугольника АВС в положение, когда фронталь BD окажется перпендикулярной оси x Горизонтальные проекции точек А и С перемещаются параллельно оси x, точка В неподвижна. Плоскость преобразована в горизонтально проецирующую, проекция А 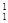 В
В 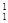 С
С 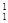 – прямая линия.
– прямая линия.
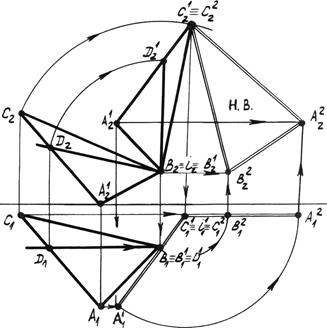
Рис. 5.8. Определение натуральной величины
плоскости (АВС) способом вращения
Вторым вращением вокруг оси i1, перпендикулярной плоскости p1 и совпадающей с точкой С преобразуем треугольник во фронтальную плоскость уровня. Проведём горизонтальную проекцию А 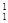 В
В 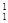 С
С 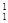 до положения параллельно оси x, А
до положения параллельно оси x, А 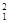 В
В 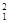 С
С 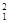 || x. На фронтальной проекции точки А и В перемещаются параллельно оси x, точка С – неподвижна. Новая фронтальная проекция А
|| x. На фронтальной проекции точки А и В перемещаются параллельно оси x, точка С – неподвижна. Новая фронтальная проекция А 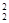 В
В 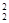 С
С 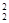 является натуральной величиной треугольника АВС.
является натуральной величиной треугольника АВС.
Дата добавления: 2015-09-11; просмотров: 1262;
