Смеси идеальных газов. В качестве рабочих тел в технике могут использоваться смеси, состоящие из нескольких газов
В качестве рабочих тел в технике могут использоваться смеси, состоящие из нескольких газов. Если смесь состоит из идеальных газов, то для неё справедливы все соотношения, полученные для однородного идеального газа. Так уравнение состояния для 1 кг смеси идеальных газов имеет вид:
pv = R 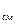 T . (4.1)
T . (4.1)
Для G кг смеси –
pV = G R 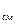 T , (4.2)
T , (4.2)
где R 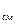 - газовая постоянная смеси, Дж / (кг
- газовая постоянная смеси, Дж / (кг  град) .
град) .
Для 1 кмоль смеси –
pV 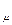 = R
= R 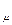 T . (4.3)
T . (4.3)
Здесь V 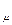 = v
= v 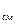
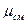 - объём 1 кмоль смеси;
- объём 1 кмоль смеси;
v 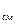 - удельный объём смеси, м
- удельный объём смеси, м 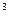 / кг;
/ кг;
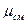 - кажущаяся или средняя молекулярная масса смеси, кг / кмоль;
- кажущаяся или средняя молекулярная масса смеси, кг / кмоль;
R 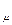 = 8314 Дж / (кмоль
= 8314 Дж / (кмоль 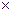 град) – универсальная газовая постоянная для смеси.
град) – универсальная газовая постоянная для смеси.
Для определения величин R 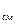 и
и 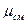 необходимо знать состав смеси, который может быть задан массовыми или объёмными долями.
необходимо знать состав смеси, который может быть задан массовыми или объёмными долями.
Массовая доля i-той составляющей газовой смеси:
g  =
= 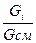 , (4.4)
, (4.4)
где G  - масса данного газа в смеси, кг;
- масса данного газа в смеси, кг;
G 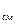 - масса смеси, кг.
- масса смеси, кг.
Сумма массовых долей:
 = 1. (4.5)
= 1. (4.5)
Каждый из газов, составляющих смесь, занимая объем, равный объему смеси, находится под своим парциальным давлением ( p  ) и имеет температуру смеси. Давление смеси равно сумме парциальных давлений. Это положение известно под названием
) и имеет температуру смеси. Давление смеси равно сумме парциальных давлений. Это положение известно под названием
закона Дальтона:
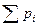 = p
= p 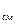 . (4.6)
. (4.6)
Объемная доля i-той составляющей газовой смеси:
r  =
= 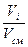 , (4.7)
, (4.7)
где V  - объём данного газа, взятый при давлении смеси, так называемый приведенный
- объём данного газа, взятый при давлении смеси, так называемый приведенный
(парциальный)объём, м  ;
;
V 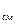 - объём смеси, м
- объём смеси, м 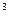 .
.
Сумма объёмных долей:
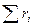 = 1. (4.8)
= 1. (4.8)
Сумма приведённых объёмов V  равна объёму всей смеси V
равна объёму всей смеси V 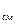 .
.
Если смесь задана массовыми долями, то R 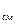 и
и 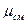 определяются из следующих соотношений:
определяются из следующих соотношений:
R 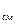 =
=  R
R  (4.9)
(4.9)
или
R 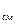 = 8314
= 8314 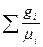 ; (4.10)
; (4.10)
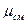 =
= 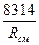 , (4.11)
, (4.11)
или
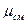 =
=  =
=  . (4.12)
. (4.12)
Если смесь задана объёмными долями, то справедливы зависимости:
R 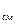 =
=  (4.13)
(4.13)
или
R 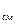 =
=  ; (4.14)
; (4.14)
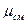 =
= 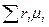 , (4.15)
, (4.15)
откуда
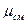 = 8314
= 8314 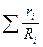 . (4.16)
. (4.16)
Парциальные давления отдельных газов, входящих в смесь, определяются из следующих соотношений:
1) если смесь задана массовыми долями, то
p  = g
= g 
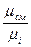 p
p 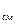 = g
= g 
 p
p 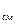 ; (4.17)
; (4.17)
2) если смесь задана объёмными долями, то
p  = r
= r  p
p 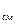 . (4.18)
. (4.18)
Соотношения между массовыми и объёмными долями составляющих газов и всей смеси в целом:
g  =
= 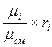 =
= 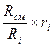 ; (4.19)
; (4.19)
r  =
= 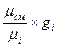 =
=  . (4.20)
. (4.20)
Вопросы для самоконтроля
1. Что такое газовая смесь?
2. Дать формулировку закона Дальтона.
3. Что называется парциальным давлением?
4. Что называется массовой, объёмной и мольной долями?
5. Что называется парциальным, или приведенным, объёмом?
6. Почему молекулярная масса смеси называется средней молекулярной массой?
7. Как производится пересчёт массового состава в объёмный и объёмного в массовый?
8. Как определяется газовая постоянная по массовым и объёмным долям?
9. Как определяется парциальное давление газа в смеси по массовым и объёмным долям?
10. Как определяется средняя молекулярная масса смеси газов?
5. Теплоёмкость газов
Теплоёмкостью называют количество тепла, необходимое для нагревания тела на один градус. Эта величина зависит от количества вещества в теле и является экстенсивным свойством.
В термодинамических расчётах используется теплоёмкость единицы количества вещества, которую называют удельной теплоёмкостью тела в данном процессе или просто теплоёмкостью. Эта величина является интенсивным параметром, т.е. удельная теплоёмкость не зависит от количества вещества в системе.
В зависимости от того, к какой количественной единице отнесена теплоёмкость, в термодинамике различаются:
1) массовая теплоёмкость c  , кДж/(кг град) – для 1 кг;
, кДж/(кг град) – для 1 кг;
2) объёмная теплоёмкость c 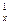 , кДж/(м
, кДж/(м 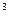 град) – для 1 м
град) – для 1 м 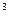 , взятого при
, взятого при
нормальных физических условиях, т.е. при давлении 101 325 Па
( 760 мм рт. ст. ) и температуре 0  С;
С;
3) мольная теплоёмкость 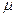 c
c  , кДж/(кмоль град) – для 1 кмоль газа.
, кДж/(кмоль град) – для 1 кмоль газа.
Между указанными выше теплоёмкостями существует следующая взаимосвязь:
c  = c
= c  v
v  =
=  =
= 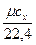 , (5.1)
, (5.1)
где v  и
и  – соответственно, удельный объём и плотность при нормальных
– соответственно, удельный объём и плотность при нормальных
физических условиях;
x – индекс, который указывает на тот параметр ( p, v и др.), при
постоянном значении которого происходит рассматриваемый процесс.
Сообщение телу теплоты в каком-либо процессе вызывает изменение его состояния и, в общем случае, сопровождается изменением температуры. Предел отношения теплоты 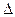 q
q  , полученной единицей количества вещества при бесконечно малом изменении его состояния, к изменению температуры
, полученной единицей количества вещества при бесконечно малом изменении его состояния, к изменению температуры 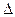 t называют истинной теплоёмкостью тела в данном процессе:
t называют истинной теплоёмкостью тела в данном процессе:
c  =
= 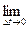
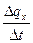 =
= 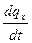 . (5.2)
. (5.2)
Фактически, это теплоёмкость при данных значениях параметров состояния v и T , или p и T (т.е. в данном состоянии тела).
В общем случае теплоёмкость не является постоянной величиной.
Для идеального газа теплоёмкость зависит от его физических свойств (прежде всего от его атомности), температуры, характера процесса, а для реальных газов – и от давления.
Иногда в теплотехнических расчётах, не требующих большой точности, особенно в области сравнительно невысоких температур и при небольших интервалах, пренебрегают зависимостью теплоёмкости от температуры и считают её величиной постоянной.
В связи с зависимостью теплоёмкости от температуры вводится понятие средней теплоёмкости в интервале температур, которой называют отношение
c 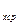 =
=  , (5.3)
, (5.3)
где q  – теплота,
– теплота,
t 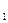 и t
и t 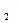 - температуры начала и конца процесса.
- температуры начала и конца процесса.
Таким образом, количество тепла в процессе нагревания или охлаждения рабочего тела можно определить, если известны средняя теплоёмкость процесса, температуры начала и конца процесса и количество вещества.
В общем случае зависимость теплоёмкости от температуры имеет нелинейный характер, поэтому каждому значению температуры соответствует своё значение истинной теплоёмкости. Эта зависимость описывается полиномом
c  = a + bt + dt
= a + bt + dt 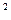 + ... , (5.4)
+ ... , (5.4)
где a, b, d, … -постоянные для каждого газа величины, определяемые на основании
экспериментальных или теоретических данных.
При нелинейной зависимости теплоёмкости от температуры вычисление средних теплоёмкостей в интервале температур t 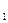 и t
и t 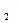 представляет значительные трудности. Поэтому, для наиболее распространённых газов определены экспериментально и приведены в справочных таблицах средние теплоёмкости в интервале от нуля до какой-либо температуры t. При этом температура t принимает различные, всё увеличивающиеся на определённый интервал (например, на 100
представляет значительные трудности. Поэтому, для наиболее распространённых газов определены экспериментально и приведены в справочных таблицах средние теплоёмкости в интервале от нуля до какой-либо температуры t. При этом температура t принимает различные, всё увеличивающиеся на определённый интервал (например, на 100  C) значения температур. Обычно в таблицах задаются значения мольных средних теплоёмкостей для процессов, протекающих при p = const и различных температурах (см. Приложение 4).
C) значения температур. Обычно в таблицах задаются значения мольных средних теплоёмкостей для процессов, протекающих при p = const и различных температурах (см. Приложение 4).
К примеру, средняя мольная теплоемкость в произвольном диапазоне температур от t 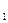 и t
и t 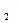 в изобарном процессе при использовании табличных данных определяется по формуле
в изобарном процессе при использовании табличных данных определяется по формуле
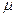 c
c  =
=  , кДж/(кмоль град), (5.5)
, кДж/(кмоль град), (5.5)
где 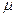 c
c  - средняя мольная теплоемкость в диапазоне температур от t
- средняя мольная теплоемкость в диапазоне температур от t 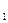 до t
до t 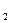 (
(  C),
C),
кДж/(кмоль град);
 - средняя мольная теплоемкость в интервале температур от 0 до t
- средняя мольная теплоемкость в интервале температур от 0 до t 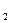
 C ,
C ,
кДж/(кмоль град);
 - средняя мольная теплоемкость в интервале температур от 0 до t
- средняя мольная теплоемкость в интервале температур от 0 до t 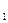
 C,
C,
кДж/(кмоль град);
t 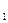 , t
, t 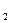 - температуры начала и конца процесса,
- температуры начала и конца процесса,  C .
C .
Тогда, средняя массовая теплоемкость в изобарном процессе определяется по формуле:
c  =
=  , кДж/(кг град), (5.6)
, кДж/(кг град), (5.6)
где 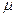 - молекулярная масса газа, кг/кмоль.
- молекулярная масса газа, кг/кмоль.
Средняя объёмная теплоемкость - по формуле:
c  =
= 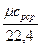 , кДж/(м
, кДж/(м 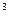 град), (5.7)
град), (5.7)
где 22,4 - объём одного моля газа в м 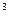 при нормальных физических условиях.
при нормальных физических условиях.
Таким образом, затраты тепла на нагревание или охлаждение рабочих тел в изобарном процессе определяются по формулам:
а) для М молей
Q  = M
= M 
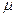 c
c 
 (t
(t 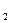 - t
- t 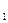 ), кДж; (5.8)
), кДж; (5.8)
б) для G кг
Q  = G
= G 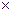 c
c 
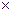 (t
(t 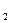 - t
- t 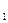 ), кДж; (5.9)
), кДж; (5.9)
в) для V м 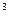
Q  = V
= V 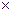 c
c 
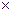 (t
(t 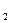 - t
- t 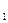 ), кДж . (5.10)
), кДж . (5.10)
В зависимости от условий, при которых происходит процесс нагревания или охлаждения рабочих тел ( p = const, v = const и т.д.), в формулах (5.8 – 5.10) указываются соответствующие значения теплоемкостей. Поэтому, для изохорного процесса расчётные зависимости для определения теплоёмкостей и количества тепла определяются по формулам:
а) для М молей
Q 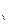 = M
= M 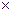
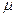 c
c 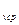
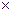 (t
(t 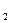 - t
- t  ), кДж, (5.11)
), кДж, (5.11)
где
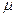 c
c 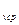 =
=  , кДж/(кмоль град);
, кДж/(кмоль град);
б) для G кг
Q 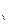 = G
= G  c
c 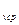
 (t
(t 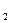 - t
- t 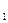 ), кДж, (5.12)
), кДж, (5.12)
где
c 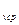 =
=  , кДж/(кг град);
, кДж/(кг град);
в) для V м 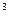
Q 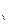 = V
= V  c
c 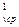
 (t
(t 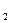 - t
- t 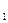 ), кДж, (5.13)
), кДж, (5.13)
где средняя объёмная теплоёмкость в инервале температур от t 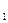 до t
до t 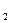 определяется с использованием табличных значений по формуле:
определяется с использованием табличных значений по формуле:
с 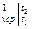 =
=  , кДж/(м
, кДж/(м 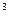 град).
град).
При расчетах количества тепла в интервале приблизительно до 1500  C можно принять зависимость теплоемкости от температуры линейной. В этом случае легко вычисляется средняя теплоёмкость в интервале температур от t
C можно принять зависимость теплоемкости от температуры линейной. В этом случае легко вычисляется средняя теплоёмкость в интервале температур от t 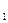 до t
до t 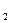 или по истинной теплоемкости:
или по истинной теплоемкости:
c  = a + bt , (5.14)
= a + bt , (5.14)
или по средней теплоёмкости в интервале температур от 0 до t  C :
C :
 = a +
= a +  t . (5.15)
t . (5.15)
В первом случае для нахождения нужной в расчётах средней теплоёмкости в интервале температур от t 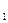 до t
до t 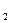 следует вместо t подставить полусумму температур 0,5( t
следует вместо t подставить полусумму температур 0,5( t 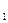 + t
+ t 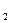 ), а во втором случае – сумму температур
), а во втором случае – сумму температур
( t 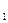 + t
+ t 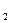 ). Таким образом, для обоих случаев получают зависимость:
). Таким образом, для обоих случаев получают зависимость:
 = a + b
= a + b 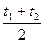 . (5.16)
. (5.16)
Коэффициенты a и b выбираются по справочным таблицам, где приводятся средние массовые и объёмные теплоёмкости различных газов (в пределах от 0 до 1500  ) при линейной зависимости их от температуры. При этом расчёт количества тепла в изохорном и изобарном процессах производится по формулам:
) при линейной зависимости их от температуры. При этом расчёт количества тепла в изохорном и изобарном процессах производится по формулам:
Q 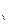 = Gc
= Gc 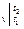
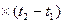 = V
= V  c
c 
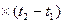 ; (5.17)
; (5.17)
Q  = Gc
= Gc 
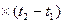 =
= 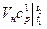
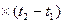 . (5.18)
. (5.18)
В зависимости от характера процесса в термодинамике имеют большое значение теплоемкости процессов при постоянном объёме (изохорная теплоёмкость – c 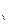 ) и при постоянном давлении (изобарная теплоёмкость – c
) и при постоянном давлении (изобарная теплоёмкость – c  ). Для идеальных газов теплоёмкости этих процессов связаны между собой следующими соотношениями:
). Для идеальных газов теплоёмкости этих процессов связаны между собой следующими соотношениями:
а) массовые теплоёмкости –
c  - c
- c 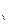 = R , (5.19)
= R , (5.19)
(это уравнение носит название уравнение Майера);
б) объёмные теплоёмкости –
c  - c
- c 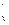 =
=  R , (5.20)
R , (5.20)
в) мольные теплоёмкости –
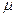 с
с  -
- 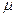 с
с 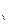 = R
= R 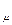 = 8,314 кДж/(кмоль град). (5.21)
= 8,314 кДж/(кмоль град). (5.21)
В теплотехнических расчётах часто приходится иметь дело не с отдельными газами, а с их смесями. При этом теплоёмкость газовой смеси определяется с помощью теплоёмкостей составляющих газов, которые выбирают из справочных таблиц.
Если смесь газов задана массовыми долями, то теплоёмкость смеси определяется как сумма произведений массовых долей на теплоёмкость каждого газа:
c  = g
= g 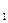 c
c 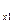 + g
+ g 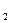 c
c 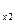 + …+ g
+ …+ g  c
c  =
= 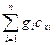 , (5.22)
, (5.22)
где g 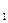 , g
, g 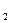 , … , g
, … , g 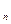 – массовые доли каждого газа, входящего в смесь;
– массовые доли каждого газа, входящего в смесь;
c 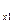 , c
, c 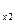 , … , c
, … , c  – теплоёмкости составляющих газов.
– теплоёмкости составляющих газов.
Если смесь газов задана объёмными долями, то объёмная теплоёмкость смеси равна сумме произведений объёмных долей на объёмную теплоёмкость каждого газа:
c  = r
= r 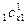 + r
+ r  + …+ r
+ …+ r 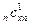 =
= 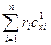 , (5.23)
, (5.23)
где r 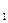 , r
, r 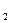 , …, r
, …, r 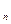 – объёмные доли отдельных газов, входящих в смесь.
– объёмные доли отдельных газов, входящих в смесь.
Если смесь газов задана мольными долями, то её мольная теплоёмкость составит:
 = r
= r  + r
+ r  + …+ r
+ …+ r 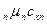 =
=  , (5.24)
, (5.24)
где  ,
,  , … ,
, … ,  – молекулярные массы отдельных газов.
– молекулярные массы отдельных газов.
Вопросы для самоконтроля
1. Дать определение массовой, объемной и мольной теплоёмкостям.
2. В каких единицах измеряются теплоемкости?
3. Что такое теплоемкость при постоянном объеме и теплоемкость при постоянном давлении?
4. Почему теплоемкость газа при постоянном давлении всегда больше теплоемкости газа при постоянном объеме?
5. Объяснить смысл всех величин, входящих в уравнение Майера.
6. Дать определение средней теплоемкости.
7. Что такое истинная теплоемкость?
8. Написать уравнение количества теплоты, выраженное через среднюю теплоемкость.
9. Как определяются величины Q 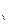 и Q
и Q  с использованием таблиц теплоемкостей?
с использованием таблиц теплоемкостей?
10. Чем отличаются теплоемкости идеальных и реальных газов?
11. Как определить среднюю теплоемкость в интервале от 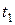 до
до 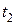 , пользуясь таблицами теплоемкостей от 0 до t° С?
, пользуясь таблицами теплоемкостей от 0 до t° С?
Дата добавления: 2015-09-02; просмотров: 1316;
