Переставна властивість дії додавання.
Ознайомлення з переставним законом додавання здійснюється через співставлення рівностей, що складено за карткою «доміно» і підводимо дітей до формування закону на підставі індуктивних міркувань.

За числовими фігурами складіть рівності на додавання. Прочитайте рівності. Що цікавого помітили? (Перший доданок став другим, а другий доданок став
5+4=9 першим, значення суми від цього не змінилося).
4+5=9
Висновок: При додаванні числа можна переставляти.
Розглядаємо переставну властивість додавання для трьох доданків.
Розгляньте рівності. Чим вони схожі, чим відрізняються. Який висновок можна зробити?
2+3+4=9 4+3+2=9 3+4+2=9
Висновок:
Додавати числа можна в будь-якому порядку, значення суми від цього не зміниться.
Переставний закон додавання застосовується для визначення значень виразів.
1) Порівняйте суми. Чим вони схожі? Чим відрізняються? Що можна сказати про результати сум? Чому?
5+3+2 9+1 6+3+1
2+3+5 1+9 6+1+3
2) Порівняйте записи в кожному стовпчику. Чи допоможе перша рівність обчислити значення другого виразу? Чому? Знайдіть значення другого виразу в кожному стовпчику.
5+2=7 4+2=6 3+2=5 9+1=10 4+5=9
2+7= 2+4= 2+3= 1+9= 6+4=
Значення якої суми не змогли знайти?
3. Послідовність вивчення усного додавання і віднімання двоцифрових чисел без переходу через десяток в межах 100. Особливості організації диференційованої роботи при вивченні одного з обчислювальних прийомів
1. Методика вивчення усного додавання без переходу через десяток.
Вивчення теми «Усне додавання двоцифрових чисел без переходу через десяток» відбувається у 1 класі в такій послідовності: загальний випадок 34+52; окремі випадки 54+30, 54+3, 20+47; обчислення виду 53+45 – двома способами. Загальним прийомом усного додавання двоцифрових чисел є прийом порозрядного додавання. Теоретичною основою прийому є принцип десяткової системи числення та переставна і сполучна властивості дії додавання. У 1 класі сполучна властивість не формулюється. З’ясовується, що додавати або віднімати числа можна частинами. Однак варто надати і проілюструвати на числових прикладах й таке правило: при додаванні кількох чисел їх можна переставляти, об’єднувати в групи, результат додавання від цього не змінюється.
Методика роботи над кожним обчислювальним прийомом буде приблизно за однаковим планом: спочатку готують учнів до ознайомлення з прийомом, далі вводять прийом, а потім виконують вправи, спрямовані на формування вміння застосовувати прийом у різних конкретних умовах і на формуванні обчислювальної компетентності.
1.1. Розглянемо, як можна провести роботу над загальним прийомом виду 34+52.
А) Підготовчі вправи:
1) кожне з чисел 37, 45, 81 запишіть у вигляді суми за зразком 43=40+3;
2) знайдіть значення виразів : 40+30; 50+20;
3) знайдіть значення виразів: 8+1; 4+5; 6+2;
4) користуючись переставною властивістю додавання, обчисліть значення виразів:
40+3+20+5; 30+2+50+4; 30+4+50+2.
Знаходячи значення сум чотирьох чисел, учні впевнюються, що зручніше десятки додавати до десятків, а одиниці – до одиниць; і щоб отримати кінцевий результат, треба додати отримані числа.
Б) Пояснення нового матеріалу.
- Сьогодні навчимося розв’язувати вирази виду 34+52.
Розв’яжемо цей вираз за допомогою паличок.
Перший доданок число 34 – це 3 десятки і 4 одиниці, другий доданок – число 52, це 5 десятків
і 2 одиниці.
Десятки додамо до десятків (3 д.+5 д.=8д.), одиниці додамо до одиниць (4 од. + 2 од.=6 од). Одержали число, що містить 8 десятків і 6 одиниць – це число 86.


 Запишемо розв’язання.
Запишемо розв’язання.









 34 + 52=86 або 34 + 52 = 30+4+50+2=80+6=86
34 + 52=86 або 34 + 52 = 30+4+50+2=80+6=86
 30 +4 50+2 30+4 50+2
30 +4 50+2 30+4 50+2
30+50=80
4+2=6
80+6=86
Далі складаємо алгоритм порозрядного додавання.
1. Подаю кожний доданок у вигляді суми десятків і одиниць.
2. Додаю десятки до десятків.
3. Додаю одиниці до одиниць.
4. Додаю отримані суми.
5. Читаю результат.
В) Первинне закріплення.
Здійснюється при коментуванні учнями розв’язування виразів.
Вправа 131 (1 клас).
Розгляньте записи і поясніть обчислення:
43+24=40+3+20+4=60+7=67
№ 132. Пропонуємо учням розв’язати вираз самостійно 25+71.
Учитель виділяє тих, хто швидко, правильно обчислить і пропонує завдання 1варіанта (сильні учні).
І етап
Працюють самостійно, користуючись підказкою.
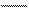

 22+46=60+8=68 35 +22=
22+46=60+8=68 35 +22=


 72+16= 18+21=
72+16= 18+21=


 61+24= 23+42=
61+24= 23+42=

З іншими учнями продовжується поетапна корекція виразів нового виду. Групова робота. На дошці записуються приклади з глибоким поясненням. Використовується паперові смужки з кружечками.
72+31= 46+52= 12+16=
Два варіанти закінчують роботу одночасно. Для тих учнів, що працювали з учителями, пропонується самостійно обчислити вираз 36+24=
Виділяються діти, яким пропонується завдання другого варіанта. На наступному етапі працюють учні 1 і 2 варіантів самостійно, а з частиною учнів – учитель.
ІІ етап
1 в. Розв’яжіть приклади, заповнивши пропуски

 34 +2 =56 71+2 =95
34 +2 =56 71+2 =95

 24+3 =57 18+4 =59
24+3 =57 18+4 =59



2 в. 27+42=60+9=69 34+22= 52+16=
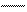



41+27= 81+14= 18+21=
З допомогою учителя учні, які не потребують допомоги, виконують аналогічні завдання, використовуючи дидактичний матеріал.
Перевірка всіх завдань. Слухають всі.
ІІІ. Етап.
1 в. Складіть 4 подібних вирази і обчисліть.
2 в. Розв’яжіть приклади, заповнивши пропуски:


 27+3 =58; 41+ 2 =67; 53 +1 = 66
27+3 =58; 41+ 2 =67; 53 +1 = 66
3 в. Обчисліть, користуючись підказкою
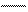

 16+32=40+8=48 45+34=
16+32=40+8=48 45+34=


 26+12= 62+14=
26+12= 62+14=
 Перевірка всіх завдань.
Перевірка всіх завдань.
Спільне завдання. Допоможіть Незнайкові відшукати помилку.
35+41=76 14+62=76 33+13=40
55+13=86 51+13=64 72+16=80
На дошці (або презентація) до уроку заготовлюється запис такого виду:
1 в.


 26+42=60+8=68 35+22=
26+42=60+8=68 35+22=


 72+16= 18+21=
72+16= 18+21=



 61+24= 23+42=
61+24= 23+42=

1 в. 2 в.



 34+2 =56 27+42=60+9=69 81+14=
34+2 =56 27+42=60+9=69 81+14=



 24+3 =57 41+27= 52+18=
24+3 =57 41+27= 52+18=



 18+ 4 =59 34+22= 18+21=
18+ 4 =59 34+22= 18+21=

 71+2 =95
71+2 =95
1 в. 2 в. 3 в.


 Складіть 4 подійних 27+3 =58 16+32=40+8=48 45+54=
Складіть 4 подійних 27+3 =58 16+32=40+8=48 45+54=



 вирази і розв’яжіть
вирази і розв’яжіть


 41+2 =67 24+12= 62+14=
41+2 =67 24+12= 62+14=

Аналогічно можна дібрати диференційоване завдання для вироблення навичків обчислення виразів іншого виду.
На другому уроці коротке пояснення.
63+25 60+20 буде 80, 3+5 буде 8 80+8=88
Отже, 63+25=88
Дата добавления: 2015-09-11; просмотров: 1276;
