Визначники третього порядку.

Означення. Визначником третього порядку називається число, що обчислюється за правилом:

.

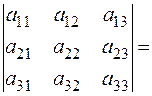
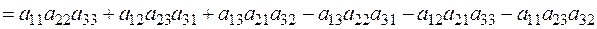Це правило називається правилом трикутників. Його зручно запам’ятати за допомогою наступної схеми:

Рис. 1.2.

Приклад. Обчислити визначник .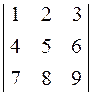

Розв’язання.

.

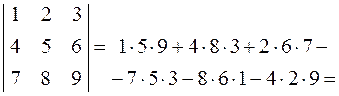
Зауваження. Для визначників третього порядку мають місце всі властивості, сформульовані для визначників другого порядку. Крім того, має місце ще одна властивість 9.

Властивість 9. Якщо усі елементи будь-якого рядка (стовпця) є лінійними комбінаціями відповідних елементів інших рядків (стовпців), то такий визначник дорівнює нулю.

Приклад. У визначника із попереднього приклада елементи першого (І) рядка можуть бути отримані як різниця подвоєного добутку елементів другого рядка та самих елементів третього рядка.

Нехай 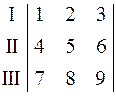. Тоді 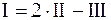, а саме: .

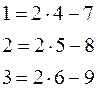Зауваження. Існує інша схема обчислення визначників третього і вищих порядків близька до метода трикутників. Ця схема називається правилом Саррюса. Полягає вона у тому, що до визначника дописують перші два стовпчики. Складають суму добутків елементів, що розташовані на діагоналях, які паралельні головній діагоналі. Від цієї суми відняти добутки елементів, що розміщені на діагоналях, паралельних побічній (рис. 1.2). Правило Саррюса можна використовувати для обчислення визначників довільного порядку n, приписуючи (n-1) стовпець.

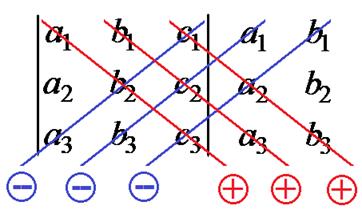
Рис. 1.2