Расчет реакторов идеального смешения
Периодического действия
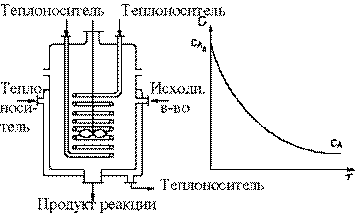
Рисунок 177 - Реакторы периодического действия.
В реакторе периодического действия все отдельные стадии процесса протекают последовательно, в разное время.
В простейшем случае реактор периодического действия состоит из сосуда с мешалкой, которая обеспечивает такое интенсивное перемешивание среды, при котором концентрация во всем объеме в любой момент времени одинакова. Теплообмен осуществляется через рубашку или змеевик.
Состав реакционной массы меняется со временем, а поэтому скорость реакции изменяется в течение процесса.
Как видно из рисунка 177 с течением времени концентрация реагента А уменьшается от начального значения 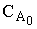 до значения
до значения 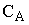 , соответствующего требуемой степени превращения. Так как на единицу объема реагирует
, соответствующего требуемой степени превращения. Так как на единицу объема реагирует 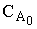 -
- 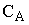 из общего количества
из общего количества 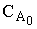 молей, то глубина превращения может быть определена как
молей, то глубина превращения может быть определена как
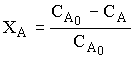 , (12.7)
, (12.7)
Время пребывания реагента в реакторе можно найти следующим образом. Обозначим через 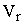 - объем реакционной массы,
- объем реакционной массы, 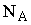 - число молей реагента А.
- число молей реагента А.
Процесс протекает во времени. Тогда по материальному балансу для исходного компонента А найдем.
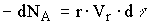 , (12.8)
, (12.8)
где r - скорость реакции, с-1.
Поскольку
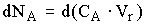 , (12.9)
, (12.9)
То с учетом выражения (12.9) уравнение материального баланса (2.8) заменяется
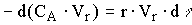 , (12.10)
, (12.10)
или
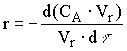 , (12.11)
, (12.11)
В общем случае для реакции любого n-ого порядка скорость реакции r с учетом выражения (12.7) можно представить
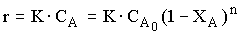 , (12.12)
, (12.12)
И тогда уравнение (12.11) примет вид:
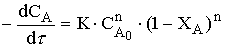 , (12.13)
, (12.13)
Выражая 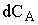 через степень превращения
через степень превращения  получим
получим
 , (12.14)
, (12.14)
Подставив найденное значение 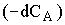 из (12.14) в (12.13) будем иметь
из (12.14) в (12.13) будем иметь
 , (12.15)
, (12.15)
Или после деления левой и правой части на С
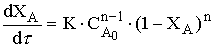 , (12.16)
, (12.16)
После интегрирования выражения (12.16) время пребывания реагентов в реакторе равно
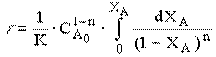 , (12.17)
, (12.17)
при  получим
получим
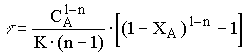 , (12.18)
, (12.18)
при n=1
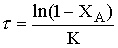 , (12.19)
, (12.19)
Реактор непрерывного действия (изотермический режим)
Этот тип реактора по устройству аналогичен реактору периодического действия. Но в реакторе непрерывного действия все отдельные стадии процесса химического превращения вещества (подача реагирующих веществ, химическая реакция, выход готового продукта) осуществляется параллельно, одновременно, непрерывно. Вследствие этого точное время пребывания частиц в зоне реакции не определено: большинство частиц из-за перемешивания проходят сложный путь до выхода из реактора. Поэтому при расчете таких реакторов истинное время пребывания компонентов в зоне реакции заменяется средним временем пребывания частиц в реакторе. Поскольку исходные материалы непрерывно подаются, а продукты реакции
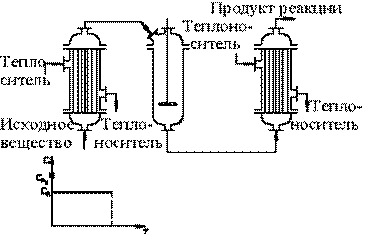
1,3 - теплообменник; 2 - реактор.
Рисунок 178 - Реактор непрерывного действия.
непрерывно отводятся, их концентрация будут постоянными в любой точке реакционного объема и в любой момент времени; также постоянной будет и скорость реакции во времени и объеме аппарата. Поэтому скорость реакции можно представить уравнением
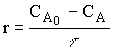 , (12.20)
, (12.20)
где 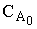 - концентрация реагента на входе в реактор;
- концентрация реагента на входе в реактор; 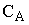 - концентрация реагента А на выходе из реактора;
- концентрация реагента А на выходе из реактора; 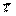 - среднее время пребывания реагента в реакторе.
- среднее время пребывания реагента в реакторе.
Величина 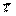 равна отношению полезного объема реактора
равна отношению полезного объема реактора 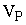 к объемному расходу V потока реагентов
к объемному расходу V потока реагентов
 , (12.21)
, (12.21)
Объем реактора, который обеспечивает требуемое падение концентрации от 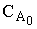 до
до 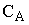 или соответствующую степень превращения, определяется из выражений (12.20) и (12.21)
или соответствующую степень превращения, определяется из выражений (12.20) и (12.21)
 , (12.22)
, (12.22)
Для реакции любого порядка с учетом выражения (12.12) и равенства (12.7) полезный объем реактора будет
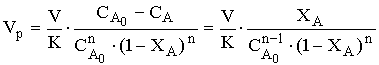 , (12.23)
, (12.23)
Для реакции 1-ого порядка уравнение (12.23) принимает вид:
 , (12.24)
, (12.24)
где  - степень превращения компонента А.
- степень превращения компонента А.
Время пребывания реагентов в реакторе найдем совместно решая уравнения (12.21) и (12.24), для реакции первого порядка
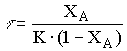 , (12.25)
, (12.25)
для реакции n-го порядка
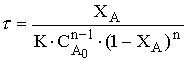 , (12.26)
, (12.26)
Дата добавления: 2015-09-11; просмотров: 1283;
