Сыпучих и связных грунтов.

Предельное напряженное состояние грунта плоскому сдвигу определяется согласно закону Кулона (см. п. 2.5). При сложном напряженном состоянии это выражается формулами:

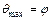и ,

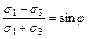где σ₁ и σ₃ – главные напряжения, действующие на трехгранную призму, вырезанную из образца при испытании его в стабилометре;

θ_max – максимальный угол отклонения.

Произведя тригонометрические преобразования для песков, уравнение предельного равновесия можно представить в часто используемом виде:

.

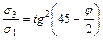Иногда условие предельного равновесия выражаются через компоненты напряжений, соответствующие координатным осям. Тогда условием предельного равновесия для связного грунта будет выражение:

.

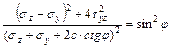Однако теория прочности Кулона, рассматривающая плоскую деформацию, не позволяет решать некоторые задачи устойчивости грунтов в основании сооружений при сложном напряженном состоянии, так как не учитывает удельного веса грунта. В связи с этим для учета нелинейной зависимости между напряжениями грунтов используют более сложные теории прочности с учетом всех компонентов напряжений.

При горизонтальной поверхности грунта, обладающего удельным весом γ, уравнения равновесия в дифференциальной форме при плоской задаче имеют вид:

; .

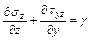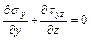Присоединяя к этим уравнениям уравнение предельного равновесия, получаем систему трех уравнений с тремя неизвестными. Следовательно, плоская задача предельного равновесия статически определима. Решение этих уравнений зависит от граничных условий.