Конструктивная и расчетная схемы простой балки
Для конкретности рассуждений рассмотрим сначала простую балку, т.е. балку на двух опорах, которые обеспечивают наиболее простое прикрепление ее к нижележащим конструкциям (колоннам, стенам).
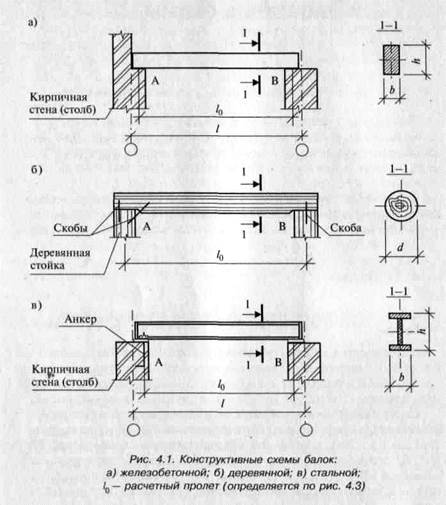
Схему балки, в которой отражены материал, форма и размеры сечения, а также специальные устройства (анкеры, болты, приварка и т.д.), будем называть конструктивной схемой балки. Нарис. 4.1 приведены конструктивные схемы железобетонной (а), деревянной (б) и стальной (в) балок, а также способы прикрепления их к нижележащим конструкциям, которые служат для балок опорами.
Конструктивные схемы по ряду причин, на которых не будем останавливаться, не дают возможности определить реакции опор и внутренние усилия в балке, поэтому введем следующие упрощения:
а) балку заменим ее геометрической осью, т.е. линией, проходящей через центры тяжести поперечных сечений. Это упрощение позволяет не рассматривать материал, форму и размеры сечения, считая, что реакции и внутренние усилия от них не зависят, а зависят только от нагрузок, действующих на балку;
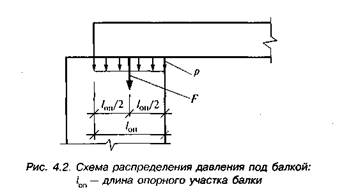
б) силу давления балки на опору F будем считать приложенной в одной точке — центре опорной поверхности. Это допущение вытекает из предпосылки, что давление балки на опору р равномерно распределено по всей опорной поверхности (рис. 4.2), на самом деле оно передается неравномерно, но учесть это трудно;
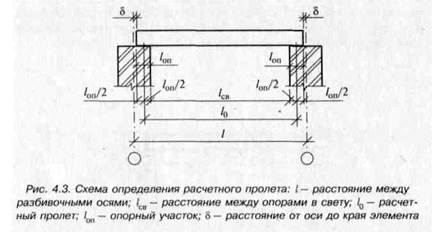
в) расстояние между серединами опорных участков считается расчетной длиной балки /,, или расчетным пролетом (рис 4.3) —
/0 = /-2(/О||/2)-25;
г) будем считать, что силы трения по плоскости контакта балки и опоры (или теперь в точке опирания балки) отсутствуют (опоры, в которых пренебрегают силой трения, называют идеальными).
Полученная на основе принятых упрощений схема балки называется ее расчетной схемой.
Таким образом, расчетная схема любой конструкции вообще и балки в частности — это идеализированное изображение конструктивной схемы, в которой не отражены свойства, незначительно влияющие на точность расчета.
Для получения расчетной схемы балок, изображенных на рис. 4.1, подробно рассмотрим их опоры. При этом также будем различать конструктивную и расчетную схемы опор балки.
Будем считать, что расчетная схема опоры соответствует конструктивной при принятых упрощениях, если они имеют одинаковые статические и геометрические (или кинематические) признаки. Под геометрическими признаками подразумевается количество независимых перемещений рассматриваемого сечения (в данном случае концов балки). Под статическими признаками подразумевается количество реактивных опорных усилий.
Покажем, как будут выглядеть расчетные схемы опор для железобетонной балки, изображенной на рис. 4.1, а. Конструктивная схема правой опоры В представлена на рис. 4.4, а. С точки зрения геометрии такая опора препятствует только вертикальному перемещению конца балки, но допускает горизонтальное перемещение (если пренебречь силами трения), и под нагрузкой происходит поворот торцевого сечения а—Ь на некоторый угол Ф|. С точки зрения статики в такой опоре возникает единственная (в рассматриваемом случае вертикальная) реакция VB по направлению перемещения, которое исключается опорой. Представим расчетную схему опоры в виде одного вертикального стержня с шарнирами по концам (рис. 4.4, б).
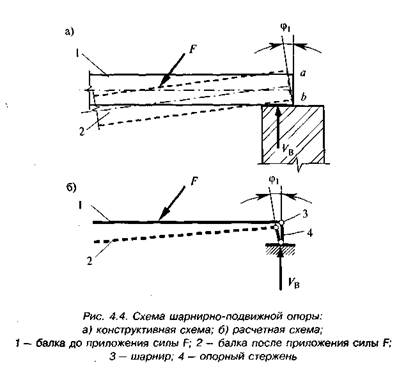
Очевидно, изображенная расчетная схема правой опоры вполне соответствует конструктивной и по геометрическим признакам, так как опорный стержень препятствует только вертикальному перемещению, и по статическим признакам, так как возникает единственная реакция по направлению опорного стержня. Такая опора (и ее расчетная схема) называется шарнирно-подвижной: шарнирной потому, что допускает поворот сечения балки на опоре, и подвижной потому, что допускает горизонтальное перемещение конца балки.
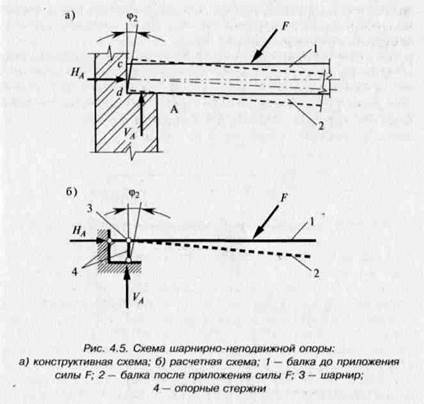
Конструктивная схема опоры А представлена на рис. 4.5, а. С точки зрения геометрии такая опора характерна тем, что препятствует вертикальному и горизонтальному перемещениям и допускает поворот сечения с—d на опоре на некоторый угол ф2. С точки зрения статики такая опора характеризуется возникновением двух составляющих реакций (ЯА и КА). Представим расчетную схему такой опоры в виде двух опорных стержней: вертикального и горизонтального (рис. 4.5, б). Полученная расчетная схема левой опоры вполне соответствует конструктивной схеме и по геометрическим признакам, так как опорные стержни препятствуют вертикальному и горизонтальному перемещениям, но не препятствуют повороту сечения, и по статическим признакам, так как по направлению каждого стержня возникает реакция. Строго говоря, возникает одна наклонная реакция, которую для удобства расчетов представляют в виде двух составляющих.
Такая опора (и ее расчетная схема) называется шарнирно-не-подвижной: шарнирной потому, что она допускает поворот сечения на опоре, и неподвижной потому, что не допускает никаких линейных перемещений конца балки.
Расчетная схема простой балки на двух опорах в целом представлена на рис. 4.6, б. Шарнирно-неподвижная опора также может изображаться в виде двух стержней, образующих треугольник (рис. 4.6, в). Оба варианта изображений опоры равноценны как с геометрической, так и со статической точки зрения.
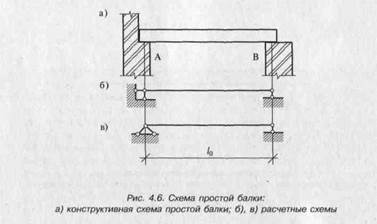
Поскольку в расчетной схеме простой балки не отражается материал, размеры, форма сечения и материал опор, ясно, что одной расчетной схеме может соответствовать несколько конструктивных схем. Например, для всех трех балок, изображенных на рис. 4.1 — железобетонной, металлической, деревянной, расчетная схема будет одна — та, что показана на рис. 4.6 (б или в).
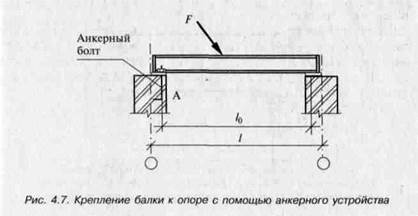
Построение расчетной схемы часто сопряжено с учетом очень многих факторов. Например, если сила Сбудет действовать не справа налево, а слева направо, как показано на рис. 4.7, то на левой опоре следует предусмотреть специальные устройства (анкеры, болты, прихватку сваркой закладных деталей балки и опоры — рис. 4.6) или поменять местами опоры. Последнее утверждение весьма условно, так как обычно опоры балки проектируются без учета направления нагрузок. Хотя в строительной практике наиболее часто встречаются вертикальные нагрузки, но опоры балки также должны обеспечивать ее неподвижность в горизонтальном направлении.
Опирание балок или плит на кирпичные стены может быть осуществлено в соответствии с рис. 4.8, а. Если исходить из принятых выше обозначений опор, то такая балка должна иметь две шарнирные неподвижные опоры (рис. 4.8, в). В реальных балочных конструкциях при таком опирании под действием нагрузки в результате деформации балки расстояние между ее концами уменьшается, не встречая сопротивления опор горизонтальным перемещениям концов балки (если нет специальных устройств, препятствующих этому перемещению), — рис. 4.8, б. Более того, между торцом балки и, например, кирпичной кладкой всегда имеется зазор. Эти обстоятельства дают возможность считать только одну (причем при вертикальной нагрузке — любую) опору неподвижной, а расчетную схему принимать по рис. 4.8, г.
Если балка опирается на стены, как показано на рис. 4.9, а, что возможно в период строительства, то в расчетной схеме следовало бы считать в соответствии с принятыми упрощениями обе опоры подвижными (рис. 4.9, б). При отсутствии трения балка пре-
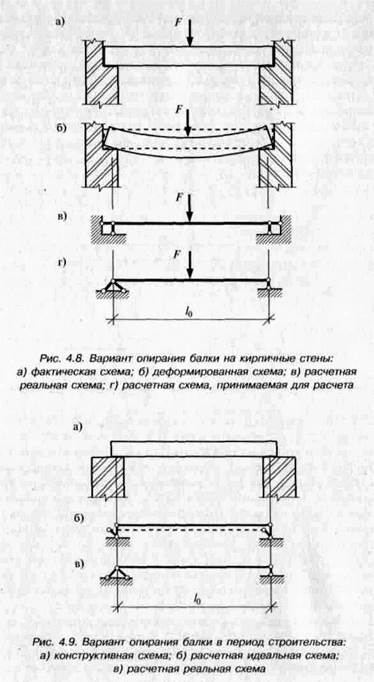
вращается в механизм, который начинает двигаться под действием незначительной случайной горизонтальной нагрузки, и поэтому не может быть конструкцией. В реальных конструкциях обязательно присутствует трение, которое обеспечивает неподвижность балки при незначительных горизонтальных нагрузках. Если они могут быть значительными, то необходимы специальные устройства, обеспечивающие неподвижность балки хотя бы на одном конце (анкеры, прихватка сваркой и т.п.). Поэтому расчетная схема такой балки может быть принята по рис. 4.9, в.
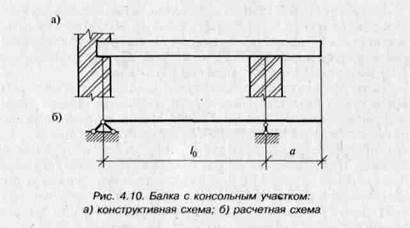
Балка на двух опорах может иметь один конец свободный (рис. 4.10, а), тогда участок балки длиной а, расположенный за опорой, называется консольным. Расчетная схема такой балки дана на рис. 4.10,б.
Опоры, показанные на приведенных рисунках, применяют для сравнительно коротких балок. Для большепролетных балок и ферм, например, мостовые опоры устраивают иначе. Это вызвано тем, что при большой длине балки ее температурные удлинения (укорочения) значительны и силы трения существенно препятствуют свободной деформации, поэтому опоры надо устроить так, чтобы по возможности уменьшить силы трения. Кроме того, специально обеспечивают свободный поворот сооружений на опорах. Опоры, обеспечивающие свободный поворот (шарнирные опоры), показаны на рис. 4.11. Правая опора выполнена подвижной (катковая опора), что обеспечивает свободу температурных деформаций.
Дата добавления: 2015-09-02; просмотров: 19498;
