Тема 5. Финансирование инновационной деятельности

ПОНЯТИЕ ФИНАНСЫОВЫХ ВЫЧИСЛЕНИЙ

Финансовые вычисления − это раздел экономико-математи­чес­кой науки, разрабатывающий методы соизмерения издержек и поступле­ний, относящихся к разным моментам времени, с учетом уровней риска. При оцен­ке собственности, в большинстве случаев, используется такой раздел финан­совых вычислений как «стандартные функции сложного процента». В настоящем параграфе пред­став­лена свод­ка основных понятий и формул, необходимых в оценоч­ной прак­тике.

В основе сложного процента лежит положение о том, что денежная сумма увеличивается пропорционально времени делового оборота и принятой ставке дохода на инвестиции. Этот процесс называется накоплением (compouding). Обратным ему является процесс дисконтирования (discounting). Используя ставку дисконта и время делового оборота, можно пересчитать известную будущую сумму денежных поступлений в эквивалентную текущую стоимость инвестиций, необходимых для получения анализируемых доходов.

Использование сложного процента при анализе процессов накопления и дисконтирования привело к выделению в теории и практике шести функций сложного процента, соответствующих различным схемам денежных поступлений по времени и размеру.

ОСНОВНЫЕ ФУНКЦИИ СЛОЖНЫХ ПРОЦЕНТОВ.

ПРЯМЫЕ И ОБРАТНЫЕ

В табличных формах приведены основные функции сложных процентов (таблица 5), сравнение формул сложного процента для рент пренумерандо и постнумерандо (таблица 6).

Прямые функции – будущая стоимость денежной единицы (аккумулированная сумма капитала), текущая стоимость обычного аннуитета, будущая стоимость обычного аннуитета.

Обратные функции – текущая стоимость будущей денежной единицы, взнос за амортизацию, фактор фонда возмещения.

Сводная таблица по шести функциям сложного процента

1.	Накопленная сумма единицы	PV FV $ 100 + $ 10 $110 + $11 $ 121 0 1 2	FV = PV (1 + i ) n	Показывает рост 1 р., положенного на депозит, при накоплении по сложному проценту
2.	Накопление единицы за период	FV % РМТ 1 РМТ 1 РМТ 2 РМТ 2 РМТ 3 0 1 2 3	FV = RMT	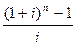Показывает, какой по истечении всего срока будет стоимость серии равных сумм по 1 р., депонированных в конце каждого из периодических интервалов
3.	Фактор фонда возмещения	FV       РМТ 1 РМТ 2	RMT = FV	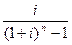Показывает сумму равновеликого периода взноса, который вместе с процентом необходим для того, чтобы к концу определенного периода накопить 1 р.
4.	Текущая стоимость единицы	$ FV PV 0 1 2 3	PV =	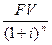Показывает текущую стоимость 1 р., который должен быть получен единовременно в будущем
5.	Текущая стоимость обычного аннуитета	РМТ 1 РМТ 2 РМТ 3 РV   0 1 2 3	PV = RMT	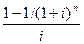Показывает текущую стоимость равномерного потока доходов. Первое поступление происходит в конце первого периода; последующее – в конце каждого последующего периода

6.

Взнос на амортизацию единицы

РМТ 1 РМТ 2 РМТ 3 РV   0 1 2 3

RMT = PV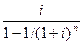

Показывает равновеликий периодический платеж, необходимый для полной амортизации кредита в 1 р.

Тема 5. Финансирование инновационной деятельности