Математическая модель потери работоспособности машиной

Определение величины наработки на отказ

Условный отказ машины наступает тогда, когда значение параметра, характеризующего техническое состояние машины, достигает предельно-допустимого значения (на рисунке 55 точка А). Считается, что в этот момент машина переходит в предотказное состояние и должна быть отправлена либо в ремонт, если отказ может быть устранён, либо на списание. Величина наработки машины в этот момент и принимается за наработку на отказ.

Модель потери работоспособности, для совокупности одноимённых машин.

Описанная выше модель (рисунок 57) справедлива для одной машины. Но в практике эксплуатации часто приходится иметь дело с совокупностью одноимённых машин. Например, в большинстве автотранспортных предприятий одновременно находиться в эксплуатации несколько автомобилей одной модели.

В таких ситуациях применима более общая модель потери работоспособности совокупности одноименных машин.

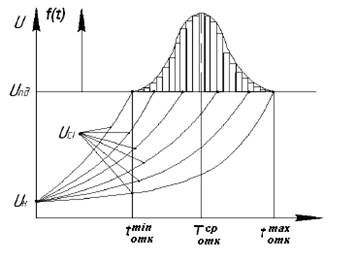
Рисунок 58 – Графическая модель потери работоспособности

парком одноименных машин

Для простоты построения модели примем ряд допущений:

- разброс значений U_н и U_пд незначителен и их значения при каждой величине наработки можно принять постоянными, равными средним значениям (U_ci);

- изменение параметра имеет постоянный характер (реализации не перемешиваются), но переменную скорость из-за большого количества факторов влияющих на машину в процессе её эксплуатации.

При этих допущениях общая графическая модель потери работоспособности машинами будет изображена в виде веерных кривых, отображающих возможные варианты изменения параметра в процессе эксплуатации (см. рисунок 58). В верхней части рисунка 58 представлена плотность распределения отказов машин (f(t)) и гистограмма.

Математическая модель потери работоспособности машиной

Как было сказано ранее, описание модели потери работоспособности машиной сводится к описанию изменения параметров, характеризующих техническое состояние машины по мере изменения наработки.

Характер изменения параметра является случайным процессом, протекающим под воздействием широкого спектра различных факторов. Известно, что наиболее полным описанием случайной функции является n - мерный закон. Однако на практике это связано с математическими трудностями [12,13].

С учетом этого, для упрощения математической модели описания процесса изменения параметра, принимается ряд допущений, а именно:

а) реализации случайного процесса изменения параметров изменяются во времени монотонно;

б) реализации не перемешиваются.

С учетом этих допущений подбирается тип аппроксимирующей функции.