Основные характеристики ферримагнитных материалов.
Классификация ферромагнитных материалов. Гистерезис.
Основные характеристики ферромагнитных материалов. Свойства ферромагнитных материалов принято характеризовать зависимостью магнитной индукции В от напряженности магнитного поля Н. Различают два основных типа этих зависимостей: кривые намагничивания и гистерезисные петли.
Под кривыми намагничивания понимают однозначную зависимость между В и Н. Кривые намагничивания подразделяют на начальную, основную и безгистерезисную (что будет пояснено далее).
Из курса физики известно, что ферромагнитным материалам присуще явление гистерезиса — отставание изменения магнитной индукции В от изменения напряженности магнитного поля Н. Он обусловлен необратимыми изменениями энергетического состояния под действием внешнего поля Н. При периодическом изменении напряженности поля зависимость между В и Н приобретает петлевой характер.
Различают несколько типов гистерезисных петель — симметричную, предельную и несимметричную (частный цикл).
На рис. 5 изображено семейство симметричных гистерезисных петель. Для каждой симметричной петли максимальное положительное значение В равно максимальному отрицательному значению B и соответственно Hmax = |-Hmax|.
Геометрическое место вершин симметричных гистерезисных петель называют основной кривой намагничивания. При очень больших Н вблизи ±Hmax восходящая и нисходящая ветви гистерезисной петли практически сливаются.
Предельной гистерезисной петлей или предельным циклом называют симметричную гистерезисную петлю, снятую при очень больших Hmax. Индукцию при Н = 0 называют остаточной индукцией и обозначают Вr.
Напряженность поля при В = 0 называют задерживающей или коэрцитивной силой и обозначают Hc.
Участок предельного цикла BrHc (рис. 1) принято называть кривой размагничивания или «спинкой» гистерезисной петли.
Этот участок используют при расчетах магнитных цепей с постоянными магнитами и магнитных элементов запоминающих устройств вычислительной техники.
Если изменять Н периодически и так, что +Hmax ≠ |-Hmax|, то зависимость между B и H будет иметь вид петли, но центр петли не совпадает с началом координат (рис. 6). Такие гистерезисные петли называют частными петлями гистерезиса или частными циклами.
Когда предварительно размагниченный ферромагнитный материал (В = 0, H = 0) намагничивают, монотонно увеличивая Н, получаемую зависимость между В и Н называют начальной кривой намагничивания.
Начальная и основная кривые намагничивания настолько близко расположены друг к другу, что практически во многих случаях их можно считать совпадающими (рис. 2).
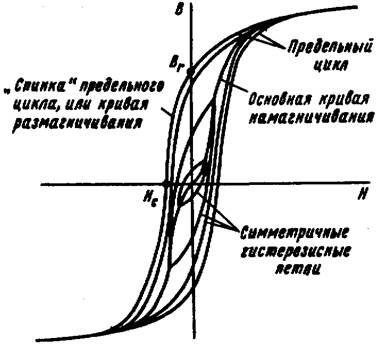
Рис. 1
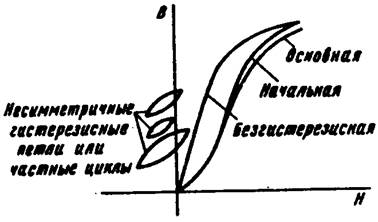
Рис. 2
Безгистерезисной кривой намагничивания называют зависимость между В и Н, возникающую, когда при намагничивании ферромагнитного материала его периодически постукивают или воздействуют на него полем, имеющим кроме постоянной составляющей еще и затухающую по амплитуде синусоидальную составляющую. При этом гистерезис как бы снимается.
Безгистерезисная кривая намагничивания резко отличается от основной кривой.
В различных справочниках, а также в ГОСТе в качестве однозначной зависимости между В и Н дается основная кривая намагничивания.
Потери, обусловленные гистерезисом. При периодическом перемагничивании ферромагнитного материала в нем совершаются необратимые процессы, на которые расходуется энергия от намагничивающего источника. В общем случае потери в ферромагнитном сердечнике обусловлены гистерезисом, макроскопическими вихревыми токами и магнитной вязкостью. Степень проявления различных видов потерь зависит от скорости перемагничивания ферромагнитного материала. Если сердечник перемагничивается во времени замедленно, то потери в сердечнике обусловлены практически только гистерезисом (потери от макроскопических вихревых токов и магнитной вязкости при этом стремятся к нулю).
Физически потери, обусловленные гистерезисом, вызваны инерционностью процессов роста зародышей перемагничивания, инерционностью процессов смещения доменных границ и необратимыми процессами вращения векторов намагниченности.
Площадь гистерезисной петли ∫HdB характеризует энергию, выделяющуюся в единице объема ферромагнитного вещества за один цикл перемагничивания.
Если ферромагнитный сердечник подвергается периодическому намагничиванию (например, в цепях переменного тока), то для уменьшения потерь на гистерезис в нем он должен быть выполнен из магнитомягкого материала.
Магнитомягкие и магнитотвердые материалы. Ферромагнитные материалы подразделяют на магнитомягкие и магнитотвердые.
Магнитомягкие материалы обладают круто поднимающейся основной кривой намагничивания и относительно малыми площадями гистерезисных петель. Их применяют во всех устройствах, которые работают или могут работать при периодически изменяющемся магнитном потоке (трансформаторах, электрических двигателях и генераторах, индуктивных катушках и т. п.).
Некоторые магнитомягкие материалы, например перминвар, сплавы 68НМП и др., обладают петлей гистерезиса по форме, близкой к. прямоугольной (рис. 3, а). Такие материалы получили распространение в вычислительных устройствах и устройствах автоматики.
В группу магнитомягких материалов входят электротехнические стали, железоникелевые сплавы типа пермаллоя и др.
Магнитотвердые материалы обладают полого поднимающейся основной кривой намагничивания и большой площадью гистерезисной петли. В группу магнитотвердых материалов входят углеродистые стали, сплавы магнико, вольфрамовые, платинокобальтовые сплавы и сплавы на основе редкоземельных элементов, например самарийкобальтовые. У последних Вr ≈ 0,9 Тл и Hc = 660 кА/м.
На рис. 3, б качественно сопоставлены гистерезисные петли для магнитомягкого материала типа пермаллоя (кривая 1) и для магнитотвердого материала (кривая 2).
Магнитодиэлектрики и ферриты. В радиотехнике, где используют колебания высокой частоты, сердечники индуктивных катушек изготовляют из магнитодиэлектриков или ферритов.
Магнитодиэлектрики — материалы, полученные путем смешения мелкоизмельченного порошка магнетита, железа или пермаллоя с диэлектриком. Эту смесь формуют и запекают. Каждую ферромагнитную крупинку обволакивает пленка из диэлектрика. Благодаря наличию таких пленок сердечники из магнитодиэлектриков не насыщаются; μr их находится в интервале от нескольких единиц до нескольких десятков.
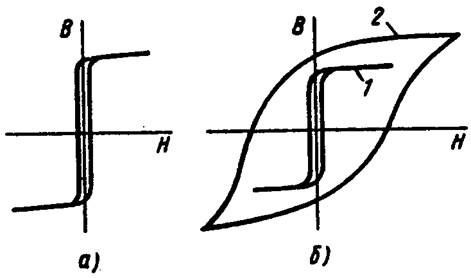
Рис. 3
Ферриты — ферримагнитные материалы. Магнитомягкие ферриты изготовляют из оксидов железа, марганца и цинка или из оксидов железа, никеля и цинка. Смесь формуют и обжигают, в результате получают твердый раствор. По своим электрическим свойствам ферриты являются полупроводниками. Их объемное сопротивление ρ = 1 ÷ 107 Ом•м, тогда как для железа ρ ~ 10-6 Ом • м.
Можно получить ферриты с различными магнитными свойствами. В отличие от магнитодиэлектриков ферриты могут насыщаться. Коэрцитивная сила магнитомягких ферритов составляет примерно 10 А/м. Маркируют их буквами и цифрой. Например, феррит 6000 НМ означает никель-марганцевый феррит, у которого на начальном участке кривой намагничивания μr = 6000. Магнитотвердые ферриты выполняют на основе феррита бария. Например, у феррита ЗБА Вr = 0.38 Тл; Нc = 145 А/м.
Закон полного тока
Магнитное поле создаётся энергетическими потоками; количественная связь между линейным интегралом от вектора напряжённости магнитного поля 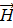 вдоль любого произвольного контура и алгебраической суммой
вдоль любого произвольного контура и алгебраической суммой 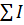 , охваченных этим контуром, определяется законом постоянного тока:
, охваченных этим контуром, определяется законом постоянного тока:
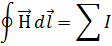
Положительное направление интегрирования d 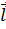 связанно с положительным направлением тока
связанно с положительным направлением тока 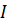 , правилом правого винта
, правилом правого винта
МДС(F) – называется произведение числа витков катушки W и протекающей по ней ток 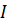 .
.
МДС W 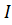 – вызывает магнитный поток в магнитной цепи подобно тому, как МДС вызывает электрический ток в электрической цепи.
– вызывает магнитный поток в магнитной цепи подобно тому, как МДС вызывает электрический ток в электрической цепи.
Как и ЭДС МДС величина направленная.
Положительное направления МДС совпадает с движением острия правого винта. 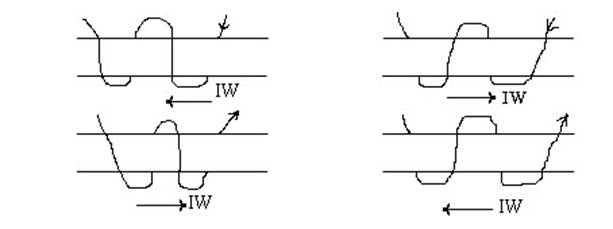
Для определения положительного направления МДС надо: если сердечник мысленно охватить правой рукой, расположить пальцы по току в обмотке, а затем отогнуть большой палец, то большой палец укажет направления МДС.
Разновидности магнитных цепей.
Магнитной цепью (М.Ц.) – называется совокупность МДС, ферромагнитных или иных тел или сред, по которой может замыкаться магнитный поток (М.П.).
М.Ц. – 1стр разветвленные и неразветвленные.
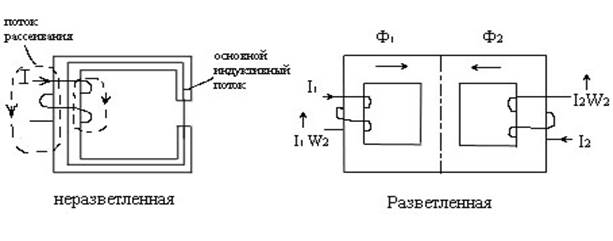
Разветвленная М.Ц. делится на симметричные и несимметричные .
Симметричная М.Ц. (см. рис.), где поток 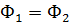 если обе части её, расположенные слева и права от вертикальной пунктирной линии, будут одинаковы в геометрическом отношении, изготовлены из одного и того же материала и при условии
если обе части её, расположенные слева и права от вертикальной пунктирной линии, будут одинаковы в геометрическом отношении, изготовлены из одного и того же материала и при условии

И потоки 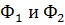 будут направлены встречно, в противном случае М.Ц. несимметрично.
будут направлены встречно, в противном случае М.Ц. несимметрично.
Роль ферромагнитных материалов.
Электрические машины, тр-ры и так далее, коммутируют ток, чтобы М.П. в них был большим.
Если в М.Ц. входит ферромагнитный материал, то поток в М.Ц. при одной и той же МДС и одинаковой геометрии цепи во много раз большим, чем при отсутствии ферромагнитного материала.

Пусть R=10 см, поперечное сечение S = 2 см2, W = 200, пропустим ток I = 1A.
Найдём потоки в теле сердечника по закону полного тока, напряженность поля не зависит от материала:

Магнитное поле в ферромагнитном сердечнике.
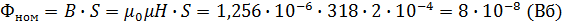
Для ферромагнитного сердечника «В» находим по кривой
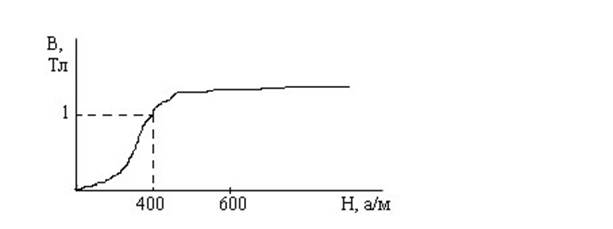
1=>В
В=>1,02(Тл)
А/М
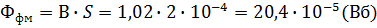
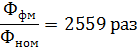
Кроме усиления потока ферромагнитным сердечником в М.Ц. сосредотачивает магнитное поле в определённой области пространства и придает ему определённую конфигурацию.
Падение магнитного напряжения (М.Н.)
Падением М.Н. между двумя точками М.Ц. называется линейность интеграла от напряженности магнитного поля между краями участка:
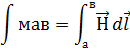
Если на этом участке 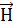 постоянна и совпадает по направлению с элементом пути
постоянна и совпадает по направлению с элементом пути 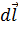 , то
, то
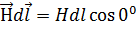
и 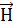 можно вывести из под знака
можно вывести из под знака 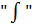
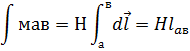
L длинна пути между точками «а» и «в»
М.Н. измеряют в [А/М]
Если несколько участков в М.Ц., то
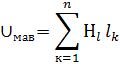
Законы Кирхгофа для М.Ц.
1-й закон Кирхгофа: алгебраическая сумма математических источников в любом узле М.Ц.=0
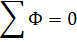
Что следует из принципа непрерывности магнитного потока (М.П.)
2-й закон Кирхгофа: алгебраическая сумма падения магнитного напряжений вдоль любого замкнутого контура равного алгебраической сумме МДС вдоль того же контура:
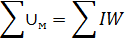
т. е эта иная запись закона полного тока.
Перед записью уравнений необходимо выбрать положительное направления Ф и отхода, если направления отхода и направления потоков совпадает, то падения магнитного напряжения в сумму 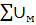 входит со знаком плюс, если нет то минус.
входит со знаком плюс, если нет то минус.
Тоже и МДС.
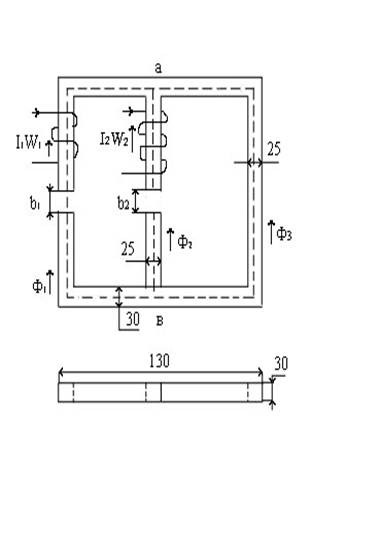 Произвольно выбранное направления потоков в ветвях(пусть всё к узлу «а»)
Произвольно выбранное направления потоков в ветвях(пусть всё к узлу «а»)
Число уравнений которые нужно составить по законам Кирхгофа, равно числу ветвей цепи (у нас - 3).
По первому закону число уравнений равно числу узлов, без единиц

По второму закону число уравнений равно числу ветвей за вычетом уравнений по 1-му закону.(3-1=2)' (обходим по часовой стрелки)
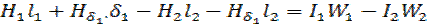

Определение МДС неразветвлённой М.Ц. по заданному потоку.
Последовательность расчета:
1) Разбиваем М.Ц. на участке постоянного сечения и определенной длины 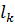 (м) и площади поперечного сечения
(м) и площади поперечного сечения 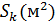 участков. Длину участков берём по средней силовой линии.
участков. Длину участков берём по средней силовой линии.
2) Исходя из постоянства потока вдоль всей цепи, по заданному потоку и сечениям Sk находим магнитные индукции на каждом участке:

3) По кривой намагничивания определим напряженность поля 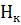 для ферромагнитных участков М.Ц. Направленность поля в в-з (
для ферромагнитных участков М.Ц. Направленность поля в в-з ( 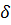 ) находим по формуле:
) находим по формуле:
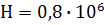 (А/М)
(А/М)
4) Подсчитываем сумму падения магнитных напряжения вдоль всей магнитной цепи 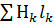 и:
и:
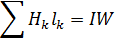
Всё это верно, если не учитывать потоки рассеяния, с увеличением « 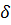 » поток рассеивания увеличивается.
» поток рассеивания увеличивается.
Пример:
Найти какой ток должен протекать в обмотке при W=500, чтобы В=1Тл
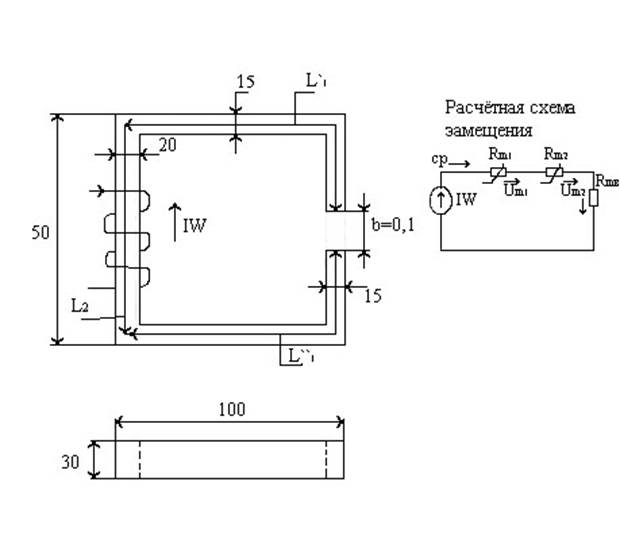
М.Ц. разбиваем на 3 участка.
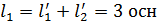
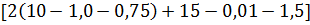
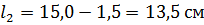
Воздушный зазор:
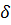 = 0,01 см
= 0,01 см
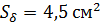
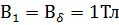 - по условию создается обмоткой
- по условию создается обмоткой
М.П.:
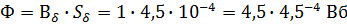
На участке «2»:
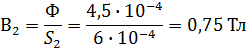
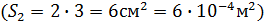
Напряженности на участках «1» и «2»: по кривым намагничивания B=f(H)

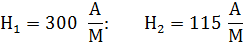
Напряженность поля в воздушном зазоре :
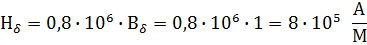
Падения магнитного напряжения вдоль всей М.Ц.:
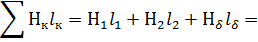
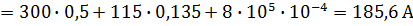
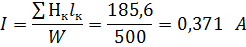
Определения М.П. в неразветвленной М.Ц. по заданной МДС.
(По предыдущему примеру)
Заданы геометрические размеры М.Ц. кривая намагничивания и полный ток, нужно найти поток и индукцию.
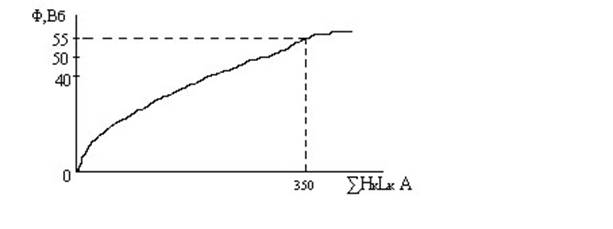
Строят зависимость Ф = f( 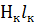 ) и найти на ней рабочую точку.
) и найти на ней рабочую точку.
Пусть IW = 350 A
Зададим значения 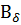 (0,5; 1,1; 1,2; 1,3 Тл) и для качественного значения подсчитываем
(0,5; 1,1; 1,2; 1,3 Тл) и для качественного значения подсчитываем  , и всё делаем как в предыдущий задачи, в результате строим зависимость Ф = f(
, и всё делаем как в предыдущий задачи, в результате строим зависимость Ф = f(  ) и по ней находим, что при IW = 350 A, Ф = 55·10-5 Вб, следовательно
) и по ней находим, что при IW = 350 A, Ф = 55·10-5 Вб, следовательно
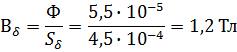
Сила тяги электромагнита.
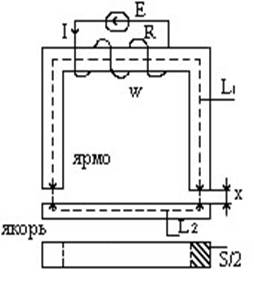 Якорь и ярмо выполнены из магнитного материала, ненасыщенный.
Якорь и ярмо выполнены из магнитного материала, ненасыщенный.
Пусть площадь сечения двух зазоров – «S»
Подсчитываем энергию М.П., заполненную в воздушном зазоре.
Магнитная энергия в воздушном зазоре.
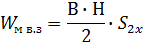
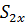 – объём воздушного зазора.
– объём воздушного зазора.
Насыщенность поля в якоре и ярме во много раз меньше, Нδ при одной и той же индукции, тогда
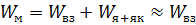
Подсчитаем силу при насыщенности М.П. исходя из 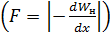
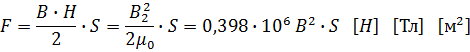
Пример:
R = 13,8 Ом, W = 900, F = 981 Н, S = 2·20 = 40 см2, l1 = 55 см, x = 0,2 см, l2 = 15 см, якорь и ярмо из одного ферромагнитного материала.
Определить ЭДС Е. т. к
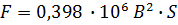 , то
, то
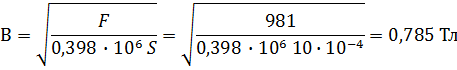
По закону полного тока
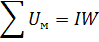
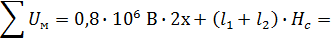
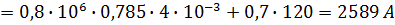
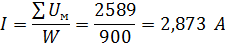
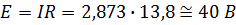
Дата добавления: 2015-11-18; просмотров: 3479;
