Совокупность (1) и (2) позволяет составить дифференциальные уравнения движения механической системы.
Составим выражение для кинетической энергии системы Т как функцию обобщенных скоростей 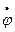 и
и 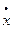 и обобщенных координат
и обобщенных координат 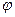 и
и 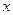 .
.
Кинетическая энергия системы равна сумме кинетической энергии Т1 звена Ι и Т2 звена 2.
Кинетическая энергия звена Ι, совершающего плоское движение:
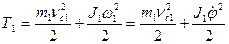 ,
,
где 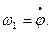
Учитывая, что 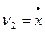 кинетическая энергия звена 2, совершающего плоское движение равна:
кинетическая энергия звена 2, совершающего плоское движение равна:
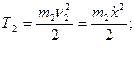
Продифференцировав по времени выражение (1) будем иметь:
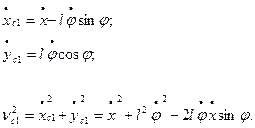
Тогда
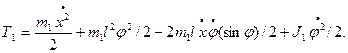
Таким образом:
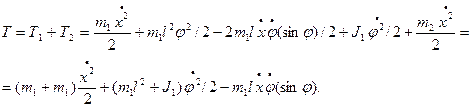
Найдем значения слагаемых уравнений Лагранжа:
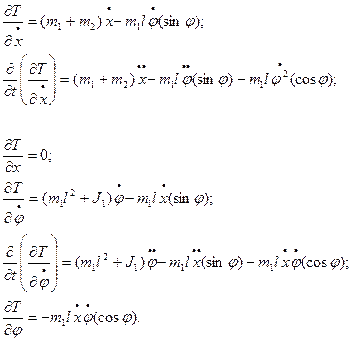
Определим обобщенные силы 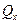 и
и 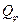 .
.
Для определения 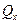 мысленно наложим на систему связь
мысленно наложим на систему связь 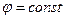 , сообщив системе возможную скорость
, сообщив системе возможную скорость 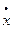 , вычислим возможную мощность сил, действующих на нее:
, вычислим возможную мощность сил, действующих на нее:
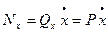
Отсюда видим:
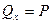
Аналогично, мысленно наложив на механическую систему связь 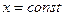 и сообщив ей возможную скорость
и сообщив ей возможную скорость 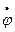 , получим выражение возможной мощности
, получим выражение возможной мощности 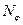 :
:
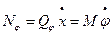
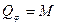
Действующие силы Qx и Qφ можно определить и из выражения работы элементарных перемещений системы, соответствующих вариации обобщенной координаты:
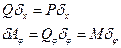
Получим:

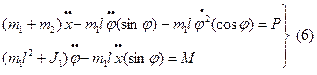
Захват D манипулятора по условию задачи должен двигаться перпендикулярно оси Х и на механизм дополнительно оказывает воздействие наложенная связь:
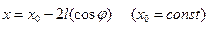
Следовательно:
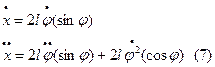
При подстановке (7) в (6), приходим к следующему соотношению:
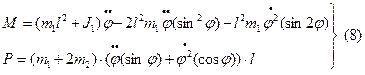
Равенства (8) представляют собой зависимость управляющего момента М и управляющего усилия Р от известных функций 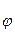 ,
, 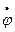 ,
, 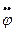 . Так как
. Так как 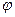 является заданной функцией времени, то вычисление производных
является заданной функцией времени, то вычисление производных 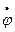 и
и 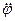 , а следовательно, и управляющего момента М и усилия Р не представляет труда.
, а следовательно, и управляющего момента М и усилия Р не представляет труда.
Определим М и Р в момент торможения звена Ι ( 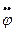 обращается в нуль, а производные соответственно равны):
обращается в нуль, а производные соответственно равны):
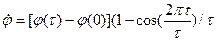

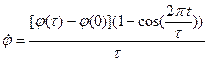 ;
;
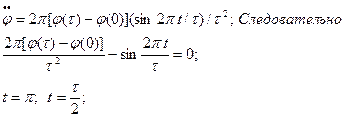
Таким образом, торможение звена Ι начинается в момент времени 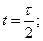
В этот момент времени:

При подстановке (9) в (8), получим:
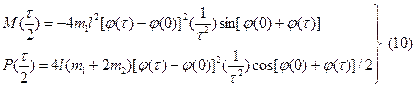
Учитывая условия задачи, имеем: 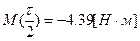 ;
; 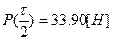
Дата добавления: 2015-11-18; просмотров: 1176;
