МАТЕМАТИЧЕСКИЕ МОДЕЛИ СРЕДСТВ ИЗМЕРЕНИЙ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ

СИ называется нестационарным, или СИ с переменными пара­метрами если его динамические свойства изменяются с течением времени. Кроме того, параметры СИ могут меняться как по времен­ной, так и по пространственной координатам. К нестационарным относятся СИ, содержащие хотя бы один преобразовательный элемент с переменными параметрами.

Факт изменения параметров во времени или пространстве корен­ным образом отличает с точки зрения динамики нестационарные СИ от стационарных. Динамика нестационарных СИ значительно" сложнее. Из нее, как простейшие частные случаи, вытекают основ­ные положения динамики стационарных СИ.

Давно известно, что к нестационарным относятся многие СИ механических и теплофизических величин. Однако сложность теорети­ческого исследования нестационарных СИ, разнообразие форм опи­сания, и, очевидно, решение других первоочередных задач в приборостроении привели к тому, что период интенсивного иссле­дования нестационарных СИ и систем следует отнести к последним десятилетиям. Поэтому сейчас еще нет установившегося мнения о том, какая форма описания является предпочтительной и более об­щей. Но наметилась тенденция к все большему применению интегрально-дифференциальных форм описания динамики [34].

Часто вопросы описания и исследования динамических свойств связываются с конкретным характером нестационарностей иссле­дуемых СИ. Используемые при этом в каждом конкретном случае методы и пути составления математической модели весьма разнооб­разны и основываются, как правило, на физических явлениях и конструктивно-технологических особенностях СИ. Некоторые приме­ры приведены в гл. 9.

Поэтому в данном параграфе рассмотрим лишь основные поло­жения о математических моделях и некоторые примеры описания нестационарных СИ в дифференциальной форме.

Следует заметить, что для составления математической модели нестационарных СИ могут быть использованы те же принципы и методы, что и для стационарных, например принцип измерительных преобразований и основанный на этом структурный метод, исполь­зование физических законов и др. Однако при этом необходимо учи­тывать нестационарность параметров преобразователей или СИ в целом, а это, естественно, приводит к усложнению как самих мето­дов, так и получаемых при этом моделей. Но это, очевидно, явля­ется закономерным, ибо разработка общих теоретических предпо­сылок нестационарных СИ является следующим шагом развития и обобщения теории стационарных СИ.

В простейшем случае нестационарное СИ с сосредоточенными параметрами может быть описано линейным дифференциальным уравнением с переменными во времени коэффициентами:

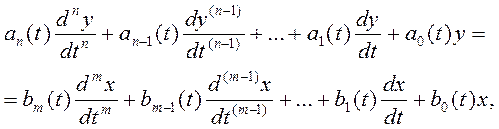(4.132)

где 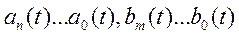— переменные во времени коэффициенты. Коэффициенты задаются либо в виде графиков и таб­лиц, построенных на основании экспериментов, либо аналити­чески.

Примером может быть уравнение простейшего ИП температуры

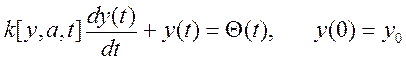(4.133)

где 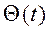— измеряемая температура; 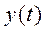— выходная величина измерительного преобразователя температуры; 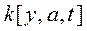— функ­ция, зависящая от текущих показаний измерительного преобразо­вателя, его конструктивно-технологических параметров, содержа­щихся в вектор-параметре а, и времени; 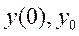— величины, определяющие начальные условия при .

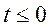Уравнением (4.133) описываются динамические свойства таких ИП, как термопары, термисторы и термометры сопротивления. Ана­логичным уравнением могут быть описаны, например, ИП давления с упругим чувствительным элементом без учета инерционности, анемометры и др. В условиях, когда 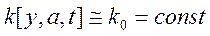, из (4.133) получим линейное дифференциальное уравнение с постоян­ными коэффициентами.

Большинство технических ИП температуры приближенно описывается уравнением [34 , 561

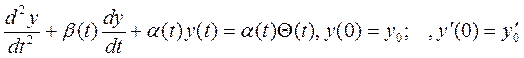(4,134)

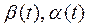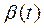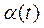где — переменные коэффициенты, характеризующие теплофизические свойства преобразователей и условия взаимодейст­вия со средой. Для и существуют приближенные аналити­ческие зависимости, вид которых зависит от конкретного техниче­ского исполнения. Кроме того, уравнение (4.134) является идеали­зированной моделью нелинейного уравнения, описывающего динамические свойства реальных ИП температуры.

Аналогично (4.134) динамические свойства ИП давления с учетом инерционности упругого элемента могут быть описаны уравнением

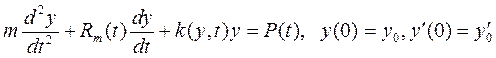_, (4.135)

где т — масса подвижных частей; у(t) — прогиб упругого элемен­та; 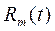— переменный коэффициент, характеризующий демпфи­рование; 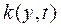— переменный коэффициент, характеризующий жесткость упругого элемента. В частности, пр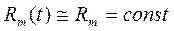и и 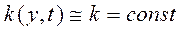R_m и k представляют коэффициенты демпфирования и жесткости, а уравнение (4.135) будет линейным дифференциальным уравнением с постоянными коэффициентами. Отсюда вытекает, что описание динамических свойств линейных ста­ционарных СИ является частным случаем нестационарных. Для линейных нестационарных СИ аналогично стационарным можно получить передаточную функцию. Однако если передаточная функция для стационарных средств измерений является универ­сальной полной динамической характеристикой и во многих случаях значительно упрощает исследования, то для линейных нестаци­онарных СИ применение передаточной функции менее эффективно, чем, например, импульсной характеристики. Поэтому для нестаци­онарных СИ передаточную функцию как динамическую характери­стику мы рассматривать не будем.

В заключение следует отметить, что для описания динамических свойств нестационарных СИ так же, как и для стационарных, могут быть использованы не только модели в виде дифференциальных уравнений типа (4.132), но и другие. Например [34], линейные мо­дели Вольтера, линейные модели Фредгольма, интегральные тож­дества, которые основываются на описании динамических свойств СИ в виде интегральных уравнений и др.