МАТЕМАТИЧЕСКИЕ МОДЕЛИ СРЕДСТВ ИЗМЕРЕНИЙ С ДИСКРЕТНЫМИ ЭЛЕМЕНТАМИ
Последнее десятилетие является периодом широкого внедрения цифровых приборов, которые обнаружили не только целый ряд преимуществ в сравнении с аналоговыми, но и обеспечили возможность использования цифровой вычислительной техники.
Методы составления математических моделей и определения основных характеристик цифровых измерительных приборов в связи с разнообразием используемых методов модуляции сигналов, аналого-цифрового преобразования и физических принципов построения являются весьма сложными и многогранными [25, 52].
СИ, содержащие дискретные элементы и микропроцессоры, могут относиться не только к цифровым измерительным приборам, но и являться частью или подсистемой информационно-измерительных систем [53], систем контроля параметров технологических процессов [34], систем управления объектами [54] и т. д. При этом использование операций дискретизации, квантования, кодирования и алгоритмов обработки информации микропроцессорами может предусматривать самые различные цели. Например, обработку результатов косвенных, совокупных или совместных измерений, коррекцию погрешностей и характеристик приборов, определение управляющего аналогового сигнала по результатам обработки информации, построение инвариантных СИ. В большинстве случаев процессы будут протекать в реальном масштабе времени. Поэтому, кроме основного уравнения цифрового измерительного прибора, определяющего зависимость между входом и выходом, и определения погрешностей квантования и дискретизации в данном случае весьма важное значение приобретают динамические характеристики. Для их определения в такой постановке задачи целесообразно воспользоваться развитой теорией импульсных систем автоматического управления.
Анализ использования ЭВМ и микропроцессоров [11, 34, 53, 54] показывает, что для описания их динамических свойств во многих случаях приемлемы разностные уравнения, дискретные передаточные функции и частотные характеристики. Вопросы полного математического описания СИ, содержащих дискретные элементы и микропроцессоры с учетом аналого-цифрового преобразования, кодирования, цифровой обработки и цифроаналогового преобразования, весьма многогранные и емкие.
Мы ограничимся лишь вопросами получения общей математической модели таких СИ в динамическом режиме. При этом основная цель — проиллюстрировать теснейшую аналогию как между методами описания и исследования, так и между характеристиками аналоговых СИ и СИ, содержащих дискретные элементы.
Для составления математической модели СИ, содержащих дискретные элементы, целесообразно, как и в случае наличия нелинейностей, выделить в нем дискретный элемент и непрерывную, или аналоговую, часть. Затем свести задачу к описанию дискретного элемента и использованию известных методов для описания линейной непрерывной части.
В соответствии с тремя возможными формами представления непрерывного во времени сигнала, квантованного по размеру, дискретного во времени, квантованного по размеру и дискретного во времени, различают три вида [55] дискретных элементов: релейные, импульсные и цифровые. Релейныеи цифровые преобразователи относятся к существенно нелинейным, так как их характеристики содержат разрывы первого рода. Методы описания таких элементов были рассмотрены в п. 4.8.
Импульсные элементы при дискретизации сигналов во времени заменяют непрерывную функцию решетчатой, которая определяется совокупностью выделенных ординат, или дискрет, модулированных по какому-либо параметру импульсной последовательности: амплитуде, ширине (длительности), периоду повторения импульсов и т. д. В соответствии с разновидностями импульсной модуляции сигналов (п. 2.5) различают амплитудно-импульсные, широтно-импульсные, время-импульсные и другие элементы. Наибольшее распространение получила амплитудно-импульсная модуляция.
Поэтому в дальнейшем ограничимся рассмотрением линейных СИ, содержащих импульсные элементы с амплитудно-импульсной модуляцией.
В этом случае реальный импульсный элемент может быть представлен в виде простейшего (идеального) импульсного элемента и формирующей цепи [33].
В случае использования в СИ ЭВМ и микропроцессоров эти устройства и будут представлять дискретную нелинейную часть. Ее в наиболее общем случае можно представить тремя блоками (рис. 4.16) — входным, центральным и выходным.
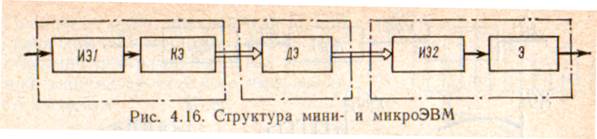
Во входном блоке производятся квантование и дискретизация сигналов по уровню и во времени. Первым элементом этого блока является импульсный элемент ИЭ1 мультиплексора, который выполняет преобразование аналогового сигнала в дискретные импульсы. Второй — кодирующий элемент КЭ — преобразует импульсы в код путем квантовании по уровню.
Центральный процессорный блок представляет собой дискретный элемент ДЭ без запаздывания. Он выполняет преобразование одного дискретного сигнала в другой в соответствии с принятым алгоритмом. Запаздыванием можно пренебречь, поскольку быстродействие, а, следовательно, и производительность современных микропроцессоров достаточно велики и несоизмеримы с периодом дискретизации сигнала.
Выходной блок состоит из нелинейного элемента, который преобразует код в последовательность импульсов; импульсного элемента ИЭ2 демультиплексора, который при необходимости разделяет каналы во времени; экстраполятора Э, который в большинстве случаев выполняет функции фиксирующего устройства, генерирующего непрерывную ступенчатую функцию.
Увеличивая число разрядов, ступень квантования можно выбрать настолько малой, чтобы результат округления практически не отличался от действительного значения величины. Это позволит при исследовании динамики не учитыватьквантование по уровню, то есть пренебречь элементами КЭ и ИЭ.
Положим, что ИЭ1 и ИЭ2 работают синхронно и синфазно. Тогда мини- или микроЭВМ и микропроцессоры могут быть представлены в виде простейшего импульсного элемента и экстраполятора. А экстраполятор можно рассматривать как аналог формирующей цепи импульсных систем.
Простейший импульсный элемент выполняет операцию дискретизации сигнала и на основании (2.85) его выходной сигнал х* (t) может быть представлен как произведение входного сигнала х (t) и немодулированной последовательности импульсов 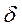 * (t):
* (t):
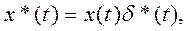 (4.112)
(4.112)
где
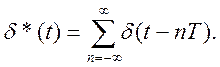
Формирующую цепь можно отнести к непрерывной части измерительной цепи.
Найдем преобразование Лапласа выходного сигнала простейшего импульсного элемента:
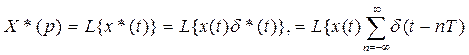 (4.113)
(4.113)
или
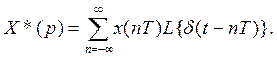
Учитывая, что  -функция, кроме точек
-функция, кроме точек  , везде равна нулю, а
, везде равна нулю, а
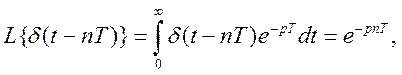
окончательно, для случая 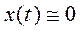 при
при 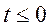 , имеем
, имеем
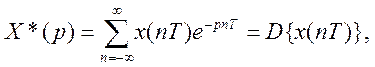 (4.114)
(4.114)
где 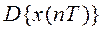 - дискретное преобразование Лапласа решетчатой или дискретной функции (рис. 2.14).
- дискретное преобразование Лапласа решетчатой или дискретной функции (рис. 2.14).
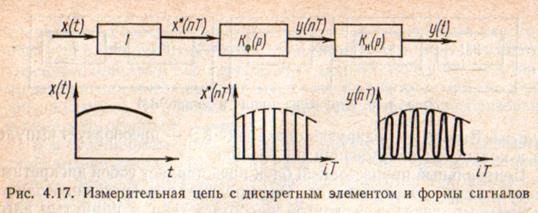
Поскольку измерительная цепь СИ (рис. 4.17) разделена на простейший импульсный элемент 1, формирующую цепь и непрерывную часть, то, зная уравнение простейшего импульсного элемента, нетрудно найти уравнение реального импульсного элемента:
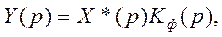
или измерительной цепи в целом:
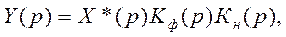 (4.115)
(4.115)
где 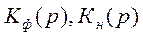 — передаточные функции формирующей цепи и непрерывной части измерительной цепи. При этом выходной сигнал реального импульсного элемента
— передаточные функции формирующей цепи и непрерывной части измерительной цепи. При этом выходной сигнал реального импульсного элемента 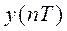 (рис. 4.17) будет представлять реакцию линейного элемента на импульсное входное воздействие, являющееся
(рис. 4.17) будет представлять реакцию линейного элемента на импульсное входное воздействие, являющееся 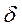 -функцией, или, что то же самое, импульсную переходную функцию h(t).
-функцией, или, что то же самое, импульсную переходную функцию h(t).
Используя выражение 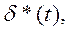 представленное рядом Фурье, на основании (4.113) получим
представленное рядом Фурье, на основании (4.113) получим
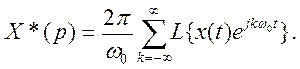
где 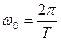 - частота, соответствующая периоду дискретизации.
- частота, соответствующая периоду дискретизации.
Справка: преобразование Фурье от 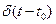
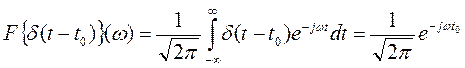
С учетом преобразований Лапласа
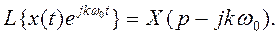
зависимость между изображением непрерывного сигнала на входе простейшего импульсного элемента X (р) и решетчатой функцией X* (р) на его выходе для 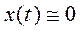 при
при 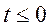
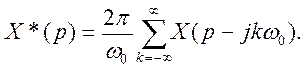 (4.116)
(4.116)
Полагая 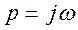 , определим из (4.116) связь между частотными характеристиками (спектрами) выходной и входной величин простейшего импульсного элемента:
, определим из (4.116) связь между частотными характеристиками (спектрами) выходной и входной величин простейшего импульсного элемента:
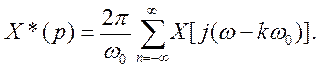 (4.117)
(4.117)
Отсюда следует, что спектр решетчатой функции равен сумме смещенных спектров входного сигнала.
Тогда, в зависимости от периода дискретизации Т или частоты 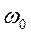 и максимальной частоты непрерывного входного сигнала
и максимальной частоты непрерывного входного сигнала 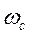 , их спектры могут перекрываться, что приводит к потере информации при восстановлении сигнала. На основании теоремы Котельникова (п. 2.4) допустимое значение периода дискретизации, не приводящее к потере информации:
, их спектры могут перекрываться, что приводит к потере информации при восстановлении сигнала. На основании теоремы Котельникова (п. 2.4) допустимое значение периода дискретизации, не приводящее к потере информации:
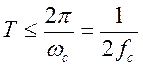
Итак, простейший импульсный элемент во временной области может быть описан уравнением (4.112), устанавливающим связь между входным непрерывным сигналом 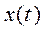 и дискретным выходным сигналом
и дискретным выходным сигналом 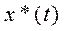 . Переход в область комплексного переменного осуществляется при помощи дискретных преобразований Лапласа. При этом изображения будут функциями
. Переход в область комплексного переменного осуществляется при помощи дискретных преобразований Лапласа. При этом изображения будут функциями 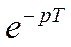 , а не переменной
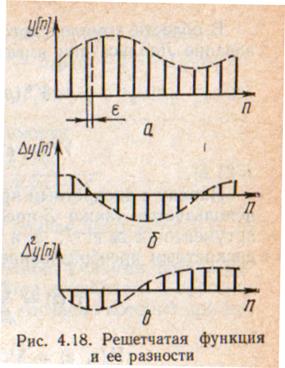
, а не переменной 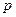 , как это имело место для непрерывных функций. Другой отличительной особенностью описания простейшего импульсного элемента является то, что для него не существует понятия передаточной функции как отношения изображений входной и выходной величин. Зависимость между выходом и входом реального импульсного элемента или измерительной цепи в области комплексного переменного может быть найдена на основании уравнений (4.115) и (4.117).
, как это имело место для непрерывных функций. Другой отличительной особенностью описания простейшего импульсного элемента является то, что для него не существует понятия передаточной функции как отношения изображений входной и выходной величин. Зависимость между выходом и входом реального импульсного элемента или измерительной цепи в области комплексного переменного может быть найдена на основании уравнений (4.115) и (4.117).
Однако как следует из уравнений (4.112) и (4.114), выходной сигнал простейшего импульсного элемента, или решетчатая функция (рис. 4.18, а), имеет значения только в моменты времени t= 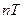 , а для времени
, а для времени 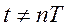 он тождественно равен нулю. Поэтому для установления значений (поведения) функции в промежутках дискретных моментов вводится смещение аргумента
он тождественно равен нулю. Поэтому для установления значений (поведения) функции в промежутках дискретных моментов вводится смещение аргумента 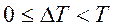 . Решетчатую функцию
. Решетчатую функцию 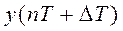 называют смещенной по отношению к
называют смещенной по отношению к 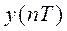 .
.
Вводя нормирование по времени 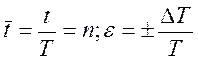 , решетчатую и смещенную функции можно представить в виде
, решетчатую и смещенную функции можно представить в виде
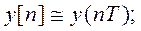
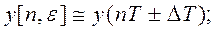 (4.118)
(4.118)
В области комплексного переменного как дискретное преобразование Лапласа они имеют вид
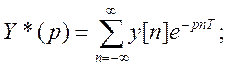
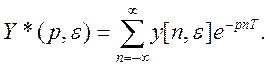 (4.119)
(4.119)
Наряду с дискретным преобразованием Лапласа (4.119), широко используется также Z-преобразование, отличающееся от первого аргументом 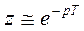 , а в остальном практически совпадающее с дискретным преобразованием Лапласа, то есть
, а в остальном практически совпадающее с дискретным преобразованием Лапласа, то есть
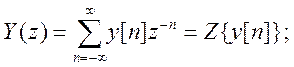
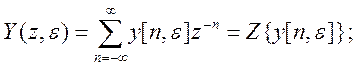 (4.120)
(4.120)
Решетчатая функция может быть описана также при помощи конечных разностей (рис. 4.18), являющихся аналогами производных непрерывных функций.
Первая разность (рис. 4.18, б) характеризует скорость изменения решетчатой функции у [п] и аналогична первой производной непрерывной функции:
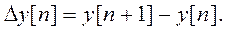
Вторую разность, или разность второго порядка (рис. 4.18, в), получаем аналогично по вычитаниям первых разностей, то есть
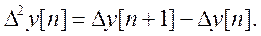
или через дискреты решетчатой функции:
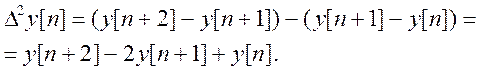 (4.121)
(4.121)
Следовательно, разность к-го порядка может быть определена как
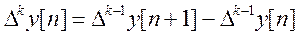 (4.122)
(4.122)
или через значения решетчатой функции:
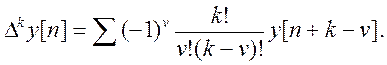 (4.123)
(4.123)
Разностные уравнения, используемые для описания преобразования в измерительной цепи решетчатых функций, представляющих входную дискретную последовательность х [n], могут быть получены на основании (4.122) через конечные разности:
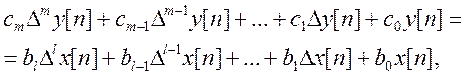 (4.124)
(4.124)
или на основании (4.123) через значения решетчатых функций:
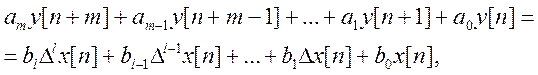 (4.125)
(4.125)
Коэффициенты 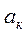 находятся из зависимости
находятся из зависимости
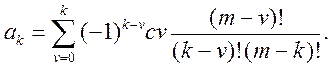 (4.126)
(4.126)
Если в уравнениях (4.125) и (4.126) правая часть 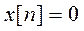 , то уравнения становятся однородными.
, то уравнения становятся однородными.
Для получения дискретной передаточной функции воспользуемся Z-преобразованием. Учитывая свойства линейности Z-преобразований [11] и применяя теорему сдвига, согласно которой при нулевых начальных условиях
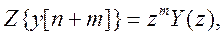
уравнение (4.126) может быть записано в алгебраической форме:
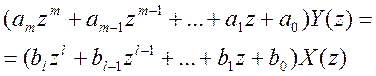
Тогда, взяв отношение изображений выходной и входной величин, получим
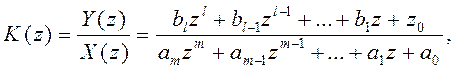 (4.127)
(4.127)
называемое при нулевых начальных условиях дискретной передаточной функцией.
Аналогично, воспользовавшись дискретным преобразованием Лапласа, может быть получена дискретная передаточная функция в форме полиномов от 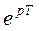 :
:
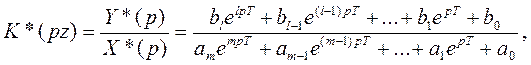 (4.128)
(4.128)
Дискретные передаточные функции (4.127) и (4.128) имеют те же значения для описания СИ, содержащих дискретные элементы или цифровую ЭВМ как элемент измерительной цепи, что и обычные передаточные функции для аналоговых СИ. Они как динамические характеристики представляют собой сокращенную запись разностных уравнений, которые описывают состояние СИ в дискретные моменты времени.
Составление разностных уравнений по дифференциальным уравнениям приведенной непрерывной части СИ довольно трудоемкий процесс. Поэтому для получения дискретной передаточной функции весьма часто используются передаточные функции непрерывной части и формирующей цепи дискретного элемента [11, 33].
Применим дискретное преобразование Лапласа к уравнению (4.115), определяющему выходной сигнал измерительной цепи:
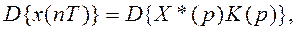 (4.129)
(4.129)
где К(р) — приведенная передаточная функция непрерывной части и формирующей цепи
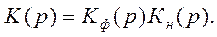
Используя теорему об умножении изображений непрерывной и решетчатой функции, согласно которой
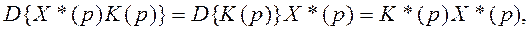
и так как
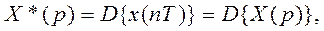
из (4.129) получим дискретную передаточную функцию
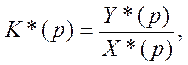 (4.130)
(4.130)
аналогичную (4.128), а при использовании Z-преобразования — (4.127).
Для измерительных цепей уравновешивающего преобразования на основании (3.21) можно показать [33], что дискретная передаточная функция в этом случае
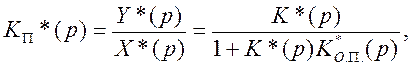 (4.131)
(4.131)
где 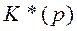 ,
, 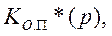 — дискретные передаточные функции прямой цени и обратного преобразователя.
— дискретные передаточные функции прямой цени и обратного преобразователя.
Частотная характеристика 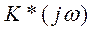 может быть получена из (4.130) или (4.131) при замене аргумента
может быть получена из (4.130) или (4.131) при замене аргумента 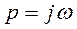 :
:
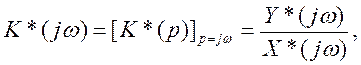
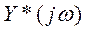 и
и 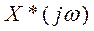 представляют собой дискретное преобразование Фурье выходного и входного сигналов.
представляют собой дискретное преобразование Фурье выходного и входного сигналов.
Таким образом, СИ, содержащие дискретные элементы, могут •быть описаны разностными уравнениями, дискретной передаточной функцией и частотной характеристикой. Эти динамические характеристики являются полными аналогами непрерывных СИ. С их использованием возможно получение частных динамических характеристик.
Если в алгоритмах обработки информации микроЭВМ или микропроцессоров необходимо учесть логические выражения или же нельзя пренебречь квантованием, длительностью импульсов и т. д., то измерительная цепь будет нелинейной. В таком случае более эффективной для описания цифровых СИ может оказаться математическая модель, полученная с использованием метода пространства состояний [54].
| <== предыдущая лекция | | | следующая лекция ==> |
| Профессиональное образование | | | МАТЕМАТИЧЕСКИЕ МОДЕЛИ СРЕДСТВ ИЗМЕРЕНИЙ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ |
Дата добавления: 2015-11-18; просмотров: 992;
