Монотонность и экстремумы функций

Определение 1. Функция 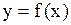называется постоянной на интервале 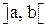, если во всех его точках она принимает одно и то же значение.

Теорема 1. Для того чтобы функция 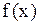была постоянной на интервале 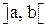, необходимо и достаточно, чтобы 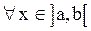выполнялось равенство .

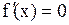Замечание. Формулировка условия необходимости в теореме 1 не содержит предположения о дифференцируемости рассматриваемой функции. Указанное свойство вытекает из того, что .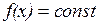

Определение 2. Функция 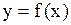называется возрастающей на интервале 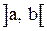, если

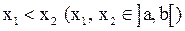
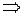
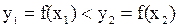
(то есть большему значению независимой переменной из рассматриваемого интервала соответствует большее значение функции).

Определение 3. Функция 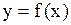называется убывающей на интервале 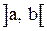, если

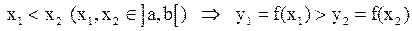
(то есть большему значению независимой переменной из рассматриваемого интервала соответствует меньшее значение функции).

График возрастающей функции простирается вправо и вверх, а график убывающей – вправо и вниз.

Определение 4. Функция 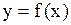называется неубывающейна интервале 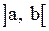, если

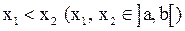
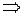
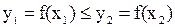
(то есть большему значению независимой переменной из рассматриваемого интервала соответствует не меньшее значение этой функции).

График неубывающей функции простирается вправо и не вверх. Ясно, что любая возрастающая функция является неубывающей. Обратное утверждение неверно.

Определение 5. Функция 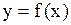называется невозрастающей на интервале 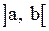, если

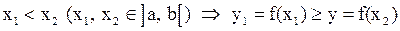
(то есть большему значению независимой переменной из рассматриваемого интервала соответствует не большее значение этой функции).

График невозрастающей функции простирается вправо и не вверх. Ясно, что любая убывающая функция является невозрастающей. Обратное утверждение неверно.

Неубывающие и невозрастающие функции объединяются термином – монотонные функции. При этом возрастающие и убывающиефункциичасто называютстрого монотонными.

Теорема 2. Если 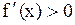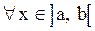, то функция 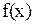возрастает на интервале .

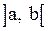Доказательство. Рассмотрим любые две точки 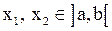такие, что 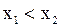. Применим к отрезку 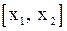теорему Лагранжа. Согласно неё найдётся по крайней мере одна точка 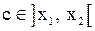такая, что выполняется равенство

.

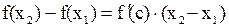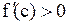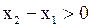Так как и , то 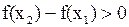. Таким образом, .

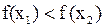Аналогично доказывается

Теорема 3. Если 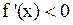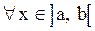, то функция 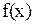убывает на интервале .

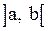Теорема 4. Для того чтобы функция 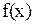была неубывающей на интервале 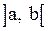, необходимо и достаточно, чтобы 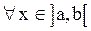выполнялось неравенство .

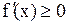Теорема 5. Для того чтобы функция 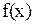была невозрастающей на интервале 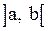, необходимо и достаточно, чтобы 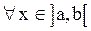выполнялось неравенство .

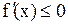Определение 6. Пусть функция 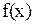определена в некоторой окрестности точки . Говорят, что 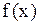имеет в точке максимум, если найдётся такая проколотая окрестность этой точки 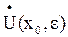, что 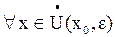выполняется неравенство

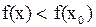. (1)

При этом называют точкой максимумафункции 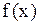, а значение функции в этой точке – максимальными пишут: .

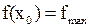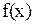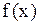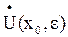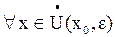Определение 7. Пусть функция определена в некоторой окрестности точки . Говорят, что имеет в точке минимум, если найдётся такая её проколотая окрестность , что выполняется неравенство

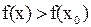. (2)

При этом называют точкой минимумафункции 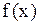, а значение функции в этой точке – минимальными пишут: .

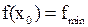Точки максимумаи точки минимумаобъединяются термином – точки экстремума функции. При этом говорят, что в точке функция 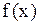имеет экстремум (достигает экстремума).

1 Необходимое условие экстремума функции

Теорема 6 (П. Ферма). Пусть – точка экстремума функции 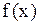. Если 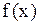дифференцируема в точке , то имеет место равенство

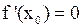. (3)

Доказательство. Предположим противное. Пусть, например, –

точка максимума функции 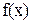и при этом 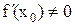. Предположим, для

определённости, что 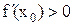. Так как

,

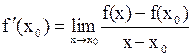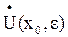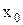то по свойству предела функции найдётся такая проколотая окрестность точки , что 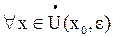выполняются одновременно два неравенства: (1) и

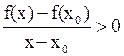. (4)

Если в указанной проколотой окрестности взять точку 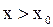, то придём к противоречию.

2 Достаточные условия экстремума функции

Выполнение равенства (2) не влечёт за собой наличия экстремума у функции 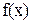в точке . В качестве контрпримера предлагается рассмотреть функцию 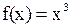в точке .

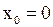Определение 8. Точка , для которой выполняется равенство (3), называется стационарной точкой (точкой, подозрительной на экстремум) функции .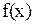

Теорема 7 (1-е правило). Пусть функция 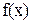дифференцируема в некоторой проколотой окрестности точки . Если 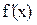меняет знак при переходе через , то – точка экстремума функции 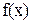. При этом, если

а) знак меняется с “ + ” на “ – ”, то – точка максимума.

б) знак меняется с “ – ” на “ + ”, то – точка минимума.

Если 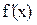не меняет знака при переходе через точку , то не является точкой экстремума функции .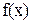

Теорема 8 (2-е правило). Пусть – стационарная точка функци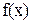и и 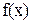имеет производную 2-го порядка в этой точке. Тогда

а) если 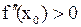, то – точка минимума функции ;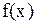

б) если 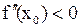, то – точка максимума функции .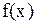

Если 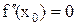, то для исследования функции 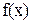на экстремум в точке нужно привлечь производные более высоких порядков.

Лекция №16

Асимптоты графика функции

Приведём сначала общее определение асимптоты линии на плоскости.

Определение 8. Пусть линия 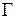содержит точки, расположенные сколь угодно далеко от начала координат. Говорят, что прямая линия 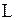является асимптотойлинии 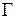, если неограниченное удаление от начала координат текущей точки 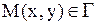влечёт за собой стремление к нулю расстояния от этой точки до , то есть (рис. 1)

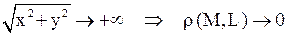. (1)

L

у

Г

х

Рис. 1

Как известно, в аналитической геометрии все прямые линии на плоскости согласно форме записи их уравнений разбивают на два класса: наклонные и вертикальные. Такая же классификация вводится для асимптот графика функции.