Покажем теперь, что равенство (1) влечёт за собой равенство
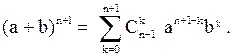
Действительно, если имеет место (1), то
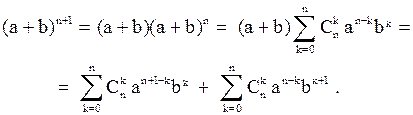
Обозначим
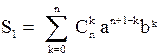 ,
, 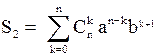 .
.
Записывая вторую сумму в виде
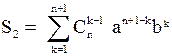 ,
,
получим:
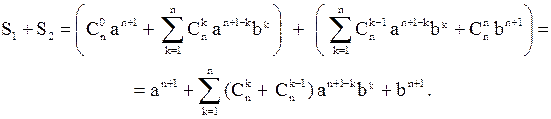
Остаётся воспользоваться непосредственно проверяемым равенством 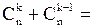
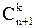
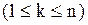 . В результате получаем:
. В результате получаем:
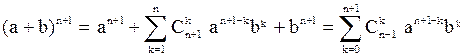 ,
,
что и требовалось доказать.
Числа 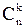 (
( 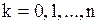 ) называются биномиальными коэффициентами.
) называются биномиальными коэффициентами.
Если в (1) положить 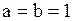 , то получим равенство
, то получим равенство
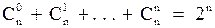 . (6)
. (6)
Оно связывает между собой все биномиальные коэффициенты при каждом фиксированном показателе степени 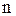 и замечательно, например, тем, что даёт ответ на вопрос о числе всех подмножеств множества, состоящего из
и замечательно, например, тем, что даёт ответ на вопрос о числе всех подмножеств множества, состоящего из 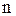 элементов. Действительно, из комбинаторики известно, что
элементов. Действительно, из комбинаторики известно, что 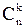 есть число всех k - элементных подмножеств такого множества (число всевозможных сочетаний из
есть число всех k - элементных подмножеств такого множества (число всевозможных сочетаний из 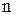 элементов по
элементов по 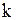 (
( 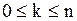 ) ). Равенство (6) означает, что число всех подмножеств такого множества (включая и пустое множество Æ) равно
) ). Равенство (6) означает, что число всех подмножеств такого множества (включая и пустое множество Æ) равно 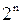 . (Соответствующий результат, естественно, без учёта Æ был получен в середине XVI в. итальянским математиком Дж. Кардано.)
. (Соответствующий результат, естественно, без учёта Æ был получен в середине XVI в. итальянским математиком Дж. Кардано.)
Лекция № 2
Понятие функции
| Часть решения осуществляется самим компьютером на основе применения аналоговых и цифровых способов, а другая часть выполняется или направляется человеком. Р.Беллман, “Математические методы в медицине”, 1983 г. |
1° Область определения, множество значений и
график функции
Определение 1. Пусть 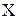 и
и 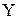 – два произвольных множества. Если каждому элементу
– два произвольных множества. Если каждому элементу 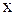
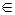
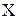 по некоторому правилу
по некоторому правилу 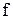 поставлен в соответствие в точности один элемент
поставлен в соответствие в точности один элемент 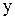
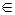
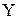 , то говорят, что на множестве
, то говорят, что на множестве 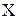 задана (определена) функция
задана (определена) функция 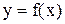 со значениями в множестве
со значениями в множестве 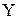 .
.
При этом пишут: 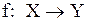 и говорят ещё, что функция
и говорят ещё, что функция 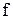 отображает множество Х в множество У.
отображает множество Х в множество У.
Элемент 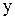 называется образом элемента
называется образом элемента 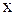 , а
, а 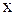 – прообразомэлемента
– прообразомэлемента 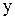 (рис.1). Множество
(рис.1). Множество 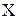 называется областью определенияфункции
называется областью определенияфункции 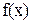 . Множество всех тех элементов
. Множество всех тех элементов 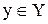 , каждый из которых является образом некоторого элемента
, каждый из которых является образом некоторого элемента 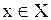 , называется множеством значений этой функции и обозначается символом
, называется множеством значений этой функции и обозначается символом 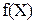 .
.
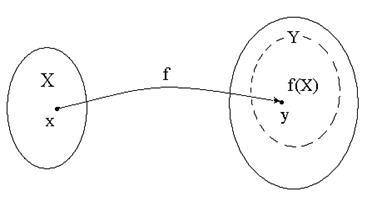
Рис. 1
Замечания.
1. Обратим внимание на единственность образа 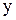 для каждого элемента
для каждого элемента 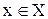 . Таким образом, постулируемое в определении 1 свойство однозначности является атрибутом понятия функции.
. Таким образом, постулируемое в определении 1 свойство однозначности является атрибутом понятия функции.
2. Имеет место включение 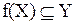 , то есть a priori множество
, то есть a priori множество 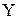 может оказаться выбранным с некоторым “запасом” по отношению к множеству значений
может оказаться выбранным с некоторым “запасом” по отношению к множеству значений 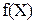 функции (рис.1).
функции (рис.1).
Правило 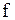 в определении функции может осуществляться различными способами. В ближайших лекциях предполагается, что
в определении функции может осуществляться различными способами. В ближайших лекциях предполагается, что 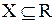 и
и 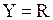 . Таким образом,
. Таким образом, 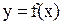 являются функциями одной независимой действительной переменной
являются функциями одной независимой действительной переменной 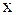 , принимающими действительные значения
, принимающими действительные значения 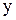 . Рассмотрим пример.
. Рассмотрим пример.
Пусть 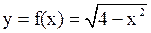 .
.
При указании области определения этой функции исходим из того, что должно выполнятся неравенство 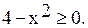 Решая его, находим что
Решая его, находим что 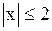 . Таким образом,
. Таким образом, 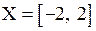 .
.
Историческая справка. До XIX века ограничивались тем, что так или иначе функцию отождествляли с некоторым аналитическим выражением, при подстановке в которое значений независимой переменной получаются соответствующие её значения. Накопление материала, как в количественном, так и в качественном отношении, привело к выявлению самой сущности рассматриваемого понятия. В результате выкристаллизовалось определение функции, заключающееся в постулировании как таковом соответствия между элементами двух множеств.
Определение 2. Графикомфункции 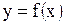 называется множество точек на плоскости вида:
называется множество точек на плоскости вида:
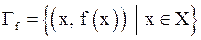 .
.
2° Взаимно однозначная и обратная функции
Определение 3. Функция 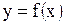 называется взаимно однозначной на множестве
называется взаимно однозначной на множестве 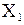 , являющемся подмножеством Х
, являющемся подмножеством Х 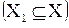 ,
,
если 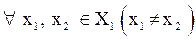 выполняется:
выполняется: 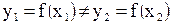 .
.
Говорят ещё, что отображение, осуществляемое функцией f , инъективнона множестве 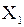 .
.
Имеется очень простой критерий взаимной однозначности функции
f: 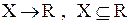 .
.
Именно, каждая горизонтальная прямая пересекает график этой функции не более чем в одной точке, имеющей абсциссу, принадлежащую 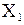 . Например,
. Например, 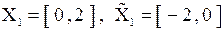 .
.
Определение 4. Пусть функция 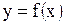 взаимно однозначна на множестве
взаимно однозначна на множестве 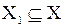 . Обратной к ней функцией называется функция, обозначаемая символом
. Обратной к ней функцией называется функция, обозначаемая символом 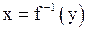 , определённая на множестве
, определённая на множестве 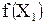 и задаваемая следующим образом.
и задаваемая следующим образом. 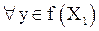 ставится в соответствие элемент
ставится в соответствие элемент 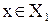 такой, что
такой, что 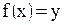 .
.
Обратная матрица осуществляет обратное отображение в случае, когда отображение задается невырожденной квадратной матрицей в соответствующем конечномерном пространстве.
Если данная функция не инъективна, обратная к ней функция не определена. Действительно, не указано, какой из элементов ( 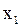 или
или 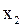 ) ставится в соответствие элементу
) ставится в соответствие элементу 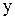 , соответствующему каждому из них при отображении f .
, соответствующему каждому из них при отображении f .
3° Сложная функция
Продемонстрируем эффективность использования в данном случае специализированных программных средств.
Задача 1 ([3], с. 31, № 210). Пусть 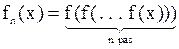 . Найти
. Найти 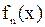 , если
, если 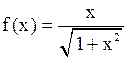 .
.
Решение. Найдём сначала выражения функций 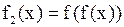 и
и
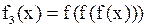 . Вводя в программу Maple выражение данной функции
. Вводя в программу Maple выражение данной функции 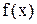 , будем иметь:
, будем иметь:
> f:=x->x/sqrt(1+x^2);
f[2]:=f(f(x));
simplify(f[2],symbolic);
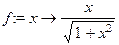
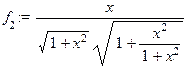
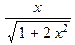
а также
>f:=x->x/sqrt(1+x^2):
f[3]:=f(f(f(x)));
simplify(f[3],symbolic);
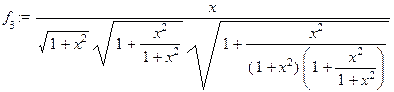
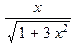
Анализируя полученные для функций 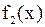 и
и 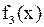 выражения, можно предположить, что имеет место формула
выражения, можно предположить, что имеет место формула
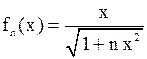
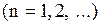 . (1)
. (1)
Докажем её методом математической индукции. Для 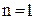 эта формула справедлива. Убедимся, что из (1) следует формула
эта формула справедлива. Убедимся, что из (1) следует формула
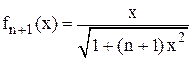 .
.
Вновь обращаясь к программе Maple, получим:
> f:=x->x/sqrt(1+x^2);
fn:=x->x/sqrt(1+n*x^2);
f(n+1):=f(fn(x)):
simplify(f(n+1),symbolic);
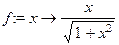
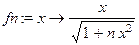
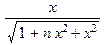
Остаётся сгруппировать слагаемые под корнем полученного выражения:
>collect(1+n*x^2+x^2,x^2);
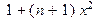
Лекция №11
Приложения дифференциального исчисления
В ряде приложений оказывается полезным понятие относительной производной функции или, как говорят в экономике, эластичностифункции.
Определение 1. Эластичностьюфункции 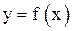 относительно независимой переменойв точке x называется число равное
относительно независимой переменойв точке x называется число равное
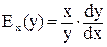 , (1)
, (1)
то есть произведению отношения независимой переменной к значению функции и производной функции в этой точке.
Для того, чтобы пояснить целесообразность введения такой функциональной характеристики, нам понадобится
Определение 2. Пусть 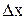 – некоторое приращение независимой переменной в точке x . Относительным приращением независимой переменной в точке
– некоторое приращение независимой переменной в точке x . Относительным приращением независимой переменной в точке 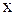 называется число
называется число 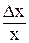 , а относительным приращением функции
, а относительным приращением функции 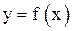 в этой точке – число
в этой точке – число 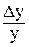 .
.
Естественно, подразумевается, что каждое из чисел 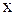 и
и 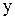 отлично от нуля.
отлично от нуля.
Предположим теперь, что 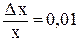 . Другими словами, пусть приращение
. Другими словами, пусть приращение 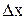 составляет 1% от числа
составляет 1% от числа 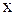 . В этом случае имеет место равенство
. В этом случае имеет место равенство
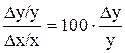 . (2)
. (2)
Сделаем простое замечание общего характера. Пусть 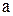 и
и 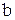 – два произвольных положительных числа. Тогда
– два произвольных положительных числа. Тогда 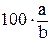 есть ничто иное, как число процентов, которое
есть ничто иное, как число процентов, которое 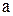 составляет от
составляет от 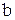 . Например, если,
. Например, если, 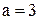 и
и 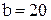 , то
, то 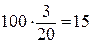 . Именно столько процентов число 3 составляет от числа 20.
. Именно столько процентов число 3 составляет от числа 20.
Возвращаясь к равенству (2), рассмотрим его правую часть. В силу сделанного замечания, она равна числу процентов, которое составит приращение 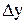 функции
функции 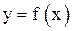 , последовавшее вслед за приращением
, последовавшее вслед за приращением 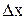 независимой переменной в точке
независимой переменной в точке 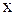 , от значения функции в этой точке. Но
, от значения функции в этой точке. Но
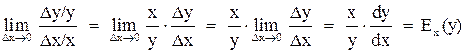 .
.
Следовательно, при малых приращениях 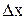 можно записать приближенное равенство
можно записать приближенное равенство
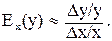
В частности, когда 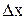 составляет 1% от
составляет 1% от 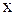 , будем иметь:
, будем иметь:
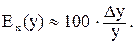
Итак, эластичность функции относительно независимой переменной приблизительно равна числу процентов, которое составит приращение функции, последовавшее вслед за увеличением независимой переменной на 1%, от исходного значения функции.
Отметим несколько необычные в среде математического анализа свойства введённого выше понятия.
Теорема 1.
(а) Эластичность произведения функций равна сумме эластичностей сомножителей.
(в) Эластичность частного функций равна разности эластичностей делимого и делителя.
Доказательство. Убедимся, например, в том, что если 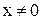 и
и 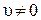 , то
, то
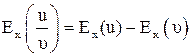 .
.
По определению эластичности функции
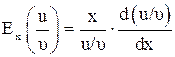 .
.
Пользуясь формулой для дифференциала частного 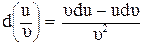 , получим:
, получим:
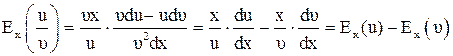 .
.
В качестве экономического приложения введённого выше понятия рассмотрим функцию 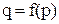 спроса относительно цены (см., например,).
спроса относительно цены (см., например,).
Так как в стабильной рыночной ситуации эта функция является не возрастающей, то имеет место неравенство 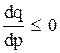 . Для того чтобы при практических вычислениях избежать отрицательных чисел, вместо
. Для того чтобы при практических вычислениях избежать отрицательных чисел, вместо 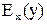 рассматривают величину, отличающуюся от неё знаком.
рассматривают величину, отличающуюся от неё знаком.
Определение 3. Эластичностьюспроса 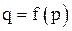 относительно цены
относительно цены 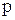 называется число, равное
называется число, равное
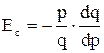 . (3)
. (3)
Таким образом, 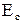 отличается знаком от соответствующей относительной производной
отличается знаком от соответствующей относительной производной 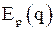 функции
функции 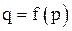 (см. (1)) и приблизительно равна числу процентов, которое составит уменьшение спроса на товар от исходного спроса, если цену на товар увеличить на 1%.
(см. (1)) и приблизительно равна числу процентов, которое составит уменьшение спроса на товар от исходного спроса, если цену на товар увеличить на 1%.
Если значения 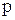 таковы, что выполняется неравенство
таковы, что выполняется неравенство 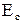 >1 , то говорят, что спрос эластичен относительно цены. В случаях, когда
>1 , то говорят, что спрос эластичен относительно цены. В случаях, когда 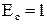 , либо, когда
, либо, когда 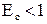 , говорят соответственно о нейтральностии неэластичности спроса относительно цены.
, говорят соответственно о нейтральностии неэластичности спроса относительно цены.
Приведём пример.
Пусть известно, что при 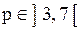 имеет место зависимость:
имеет место зависимость: 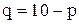 .
.
Так как 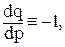 то
то 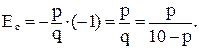 Решая уравнение
Решая уравнение 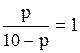 , находим, что
, находим, что 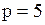 является единственной ценой, при которой спрос
является единственной ценой, при которой спрос 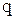 нейтрален (т.е. увеличение цены на 1% влечёт за собой падение спроса также на 1%). Соответственно получаем, что при
нейтрален (т.е. увеличение цены на 1% влечёт за собой падение спроса также на 1%). Соответственно получаем, что при 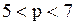 спрос эластичен, а при
спрос эластичен, а при 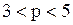 – неэластичен относительно цены. Например, если
– неэластичен относительно цены. Например, если 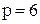 , то увеличение цены на 1% влечёт падение спроса на 1,5%.
, то увеличение цены на 1% влечёт падение спроса на 1,5%.
Лекция №12
Глобальные свойства непрерывных функций
Лемма (о стягивающихся отрезках). Пусть последовательность отрезков 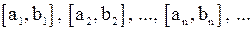 такова, что каждый последующий отрезок содержится в предыдущем и
такова, что каждый последующий отрезок содержится в предыдущем и
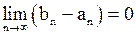 . (1)
. (1)
Тогда существует единственная точка 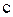 , принадлежащая каждому из этих отрезков. При этом
, принадлежащая каждому из этих отрезков. При этом
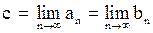 .
.
Доказательство. Рассмотрим две монотонные последовательности: и . Первая последовательность не убывает и ограничена сверху (например, числом ). Вторая не возрастает и ограничена снизу (например, числом ). Таким образом, каждая из этих последовательностей является сходящейся. Обозначим
И .
По теореме о пределе разности последовательностей получаем:
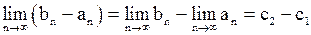 .
.
В силу предположения (1) отсюда следует, что 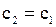 . Обозначим общий предел последовательностей
. Обозначим общий предел последовательностей 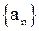 и
и 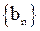 буквой
буквой 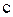 .
.
Заметим далее, что
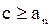 и
и 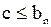
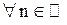 .
.
Таким образом, 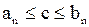
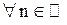 . Следовательно,
. Следовательно, 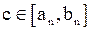
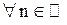 .
.
Предоставляем читателю убедиться, что не существует другой точки, отличной от точки 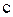 , принадлежащей всем отрезкам
, принадлежащей всем отрезкам 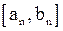 .
.
Теорема 1 (первая теорема Больцано-Коши). Пусть функция 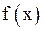 удовлетворяет условиям:
удовлетворяет условиям:
1° непрерывна на отрезке 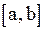 ;
;
2° 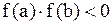 .
.
Дата добавления: 2015-11-18; просмотров: 980;
