Возрастание и убывание функции на промежутке.

Максимум и минимум

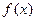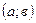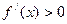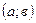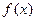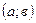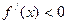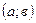Теорема 1. Пусть функция определена и дифференцируема на . Тогда если на , то монотонно возрастает на ; если на , то 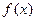монотонно убывает на .

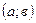Доказательство. Возьмем произвольные точки 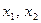. Причем 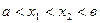. По теореме Лагранжа 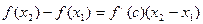, где 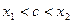. Т.к. 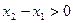, то .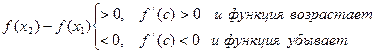

Теорема доказана.

Геометрически условие 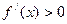означает, что угол наклона касательной острый, если 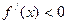- тупой.

Пример 1. .

.

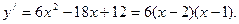
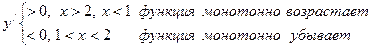Определение 1. Функция 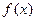в точке с имеет максимум (минимум), если существует окрестность этой точки, во всех точках 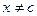которой выполняется неравенство .

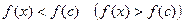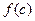- наибольшее (наименьшее) значение функции 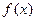в этой окрестности.

Максимум и минимум не обязательно наибольшее и наименьшее значения функции во всей области определения. Они являются таковыми лишь в соответствующих окрестностях точек. Поэтому их называют локальными (местными) максимумами и минимумами. Термины максимум и минимум объединяют под одним названием – экстремум.

Замечание 1. В определении 1 неравенства 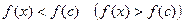являются строгими. Если их заменить более слабыми неравенствами 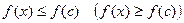, то в этом случае говорят о максимумах и минимумах в широком смысле, в отличии от строгих максимумов и минимумов в определении 1.

Теорема 2. (необходимое условие экстремума) Если функция 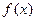, определенная в некоторой окрестности точки с, имеет экстремум в точке с, то 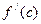либо равна нулю, либо не существует.

Доказательство. Пусть функция 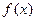определена в некоторой окрестности точки с, в которой 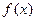имеет экстремум. Тогда существует окрестность 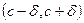, для которой 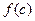является или наибольшим, или наименьшим значением. По теореме Ферма если 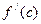существует, то 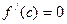. Т.о. либо 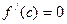, либо 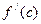не существует.

Теорема доказана.

Эта теорема является необходимым условием экстремума, т.е. экстремумы нужно искать только в тех точках, в которых 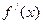либо равна нулю, либо не существует. Такие точки называются критическими. Те критические точки, в которых 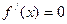называются стационарными.

Достаточным условием экстремума теорема 1 не является, т.е. не во всякой критической точке обязательно будет экстремум.

Пусть функция 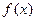дифференцируема в некоторой окрестности точки с, а в самой точке с непрерывна. Если 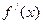на одном из двух интервалов 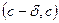, 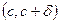положительна, а на другом отрицательна, то говорят, что 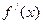при переходе х через с меняет знак.

Теорема 3. (достаточное условие экстремума) Пусть функция 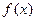дифференцируема в некоторой окрестности точки с за исключением, быть может, самой точки с, в которой 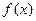непрерывна. Если 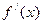при переходе х через с меняет знак, то 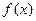в точке с имеет экстремум. Если 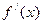меняет знак с положительного на отрицательный, то в точке с – max, а если с отрицательного на положительный – min.

Лекция 8.