Тема 4. Правило Лопиталя

Аннотация: Г. Лопиталь – французский математик, автор первого учебника по математическому анализу «Анализ бесконечно малых» (1696). В этой книге собраны и приведены в стройное целое отдельные вопросы, разбросанные до того в разных повременных изданиях, а ещё приводится Правило Лопиталя.

Ключевые слова: функция, производная, предел, неопределенность.

Методические рекомендации по изучению темы:

После изучения лекционного материала и изучения презентационного материала с разбором решений необходимо выполнить задание №4.

Источники информации:

1. Берман Г.Н. Сборник задач по курсу математического анализа / Г.Н.Берман. — М.: Наука, 1977.

2. Бугров Я.С., Никольский С.М. Дифференциальное и интегра­льное исчисление / Я.С. Бугров, С.М. Никольский.— М.: Наука, 1988.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. — М.: Высшая школа, 2001.

4. Бесплатный ресурс для студентов – http://math24.ru/calculus-list.html

5. Образовательный математический сайт – http://www.exponenta.ru/

6. Учебные материалы - http://math.fizteh.ru/study/

7. Учебные пособия - http://kpfu.ru/main_page?p_sub=14502

Список сокращений:

Глоссарий:

Абсцисса - Одна из декартовых координат точки, обычно первая, обозначаемая буквой x.

Аргумент функции - Независимая переменная величина, по значениям которой определяют значения функции.

График - Кривая на плоскости, изображающая зависимость функции от аргумента.

Дифференцирование - Термин, обозначающий нахождение, как производных функций, так и их дифференциалов.

Касательная - Предельное положение секущей, проходящей через данную точку и другую точку кривой, неограниченно приближающуюся к данной.

Константа - Постоянная величина при рассмотрении математических и других процессов.

Предел - Одно из основных понятий математики, означающее, что некоторая переменная величина в рассматриваемом процессе ее изменения неограниченно приближается к определенному постоянному значению.

Вопросы для изучения:

1. Правило Лопиталя для неопределенностей вида .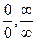

2. Правило Лопиталя для неопределенностей вида .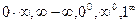

Лекция 6.

Правило Лопиталя

Пусть нужно найти предел функции, заданной формулой при стремлении аргумента к некоторой величине (к конечному числу или к ∞). Если при формальной подстановке этой величины в формулу получаем выражение 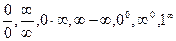, то эти выражения называются неопределенностями. Во всех этих случаях сразу нельзя сказать существует или нет предел и чему он равен.

Теорема 1. Пусть функции 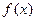и

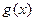
1. определены на ;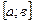

2. ;

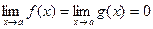3. 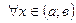существуют конечные производные 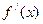и 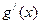, причем ;

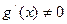4. Существует конечный или бесконечный .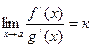

Тогда .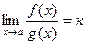

Пример 1. .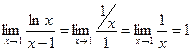

Теорема 2. Пусть функции 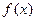и

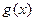
1. определены на ;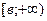

2. ;

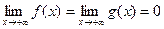3. 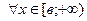существуют конечные производные 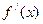и 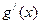, причем ;

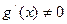4. Существует конечный или бесконечный .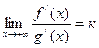

Тогда .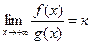

Замечание Правило Лопиталя можно использовать повторно, если каждый раз выполняются условия соответствующей теоремы.

Пример 2. .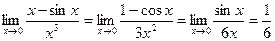

Теорема 3. Пусть функции 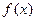и

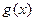
1. определены на ;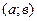

2. ;

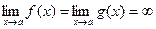3. 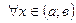существуют конечные производные 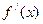и 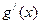, причем ;

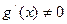4. Существует конечный или бесконечный .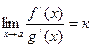

Тогда .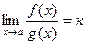

Если мы находимся в условиях применимости теорем, то пределы вычисляются согласно изложенному.

Все другие неопределенности сначала сводятся к неопределенностям вида , .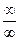

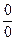1) 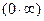. Преобразуем 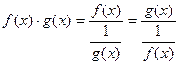. Получим, либо 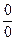, либо .

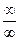2) . .

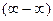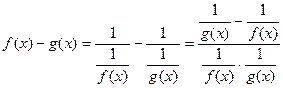3) 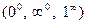. . 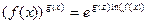Далее находим предел показателя согласно 1).

Пример 3. .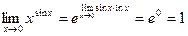

.

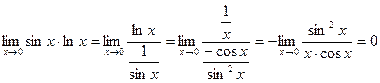Пример 4.

.

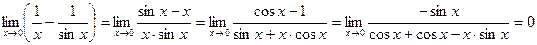Контрольные задания по теме: