Классификация по взаимодействию между частицами дисперсной фазы
(по подвижности дисперсной фазы)
Р.Зигмонди дисперсные системы разделил на свободнодисперные и связнодисперсные. В свободнодисперсных системах (золях, эмульсиях) частицы не связаны друг с другом, свободно перемещаются в дисперсионной среде под действием броуновского движения или силы тяжести. Лиозоли обладают текучестью.
В связнодисперсных системах частицы взаимодействуют друг с другом, под действием физических сил образуют пространственные сетки, структуры, поэтому не могут перемещаться. Такая система не может течь. Их называют гелями и студнями. К ним относятся пасты, концентрированные эмульсии, суспензии, пены, порошки, кремы.
Лекция 2
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЕ и ОПТИЧЕСКИЕ СВОЙСТВА КОЛЛОИДНЫХ СИСТЕМ
Молекулярно-кинетические свойства коллоидных систем, как и истинных растворов обнаруживаются в таких явлениях, как броуновское движение, диф-фузия, осмотическое давление и они связаны движением дисперсных частиц. Поскольку коллоидные частицы участвуют в тепловом движении и подчиняются молекулярно-кинетическим законам обычных растворов, экспериментально можно определить размер, массу и концентрацию частиц дисперсной фазы.
Диффузия. Диффузия – это самопроизвольный необратимый процесс вырав-нивания концентрации частиц по всему объёму раствора или газа под влиянием теплового движения. Процесс диффузии идёт самопроизвольно, поскольку он сопровождается увеличением энтропии системы, так как по второму закону тер-модинамики, равномерное распределение вещества в системе отвечает наиболее вероятному её состоянию. Для описания диффузии в коллоидных системах более справедливо применение I закона Фика:
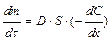 ,
,
где 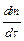 - масса вещества, диффундированного за единицу времени;
- масса вещества, диффундированного за единицу времени; 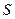 - пло-щадь диффузии,
- пло-щадь диффузии, 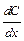 - градиент концентрации (знак «-» означает, что диффузия идёт в сторону уменьшения концентрации);
- градиент концентрации (знак «-» означает, что диффузия идёт в сторону уменьшения концентрации); 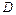 – коэффициент диффузии; это масса вещества, продиффундированного за единицу времени через единицу площади при градиенте концентрации, равном единице
– коэффициент диффузии; это масса вещества, продиффундированного за единицу времени через единицу площади при градиенте концентрации, равном единице 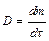 , т.е. масса вещества диффундирущего за единицу времени через поперечное сечение в 1 м2 при
, т.е. масса вещества диффундирущего за единицу времени через поперечное сечение в 1 м2 при 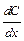 = 1 (физический смысл коэффициента диффузии).
= 1 (физический смысл коэффициента диффузии).
Эйнштейн показал, что коэффициент диффузии связан с размерами частиц, вязкости дисперсионной среды, температуры: 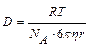 , м2/с. Как видно из формулы, чем меньше размер частиц, тем больше коэффициент диффузии. Для коллоидных систем D ~ 10-13 м2/с.
, м2/с. Как видно из формулы, чем меньше размер частиц, тем больше коэффициент диффузии. Для коллоидных систем D ~ 10-13 м2/с.
Так как в коллоидных системах размер частиц дисперсной фазы значительно больше размера молекул или ионов, скорость диффузии в коллоидных системах в целом небольшая, т.е. меньше скорости диффузии в истинных растворах.
Используя уравнение Эйнштейна можно определить размер частиц золей и молекулярную массу полимера. Для этого требуется экспериментально опреде-лить D. С этой целью, сначала оптическими методами, измеряя показатель пре-ломления или оптическую плотность раствора, измеряют скорость изменения концентрации в слое, а затем рассчитывают значение D.
В тех случаях, когда затруднено определение D через концентрацию, D и r частиц рассчитывают через смещение частиц.
После определения размера частиц можно рассчитать мицеллярную массу частиц или молекулярную массу полимера (что и было сделано впервые для белков). Для этого пользуются уравнением Перрена:
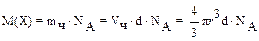 ,(а.е.м)
,(а.е.м)
где 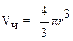 – объем одной частицы; d – плотность вещества.
– объем одной частицы; d – плотность вещества.
Дата добавления: 2015-11-12; просмотров: 1658;
