Встроенные функции VBA
VBA предоставляет большой набор встроенных функций и процедур, использование которых существенно упрощает программирование. Все функции можно разделить на следующие основные категории: математические функции, функции проверки определения и преобразования типов, преобразования форматов, обработки строк, времени и даты, финансовые функции.
Рассмотрим некоторые математические функции (табл.6).
| Таблица 6 | ||||
| Действие | Ключевое слово, синтаксис | Функция | Пример | Примечание |
| Тригонометрические вычисления | Atn (x) | Арктангенс числа | pi=4*Atn(1) | Вычисление значения pi |
| Cos (x) | Косинус угла | M=1/cos(ugol) | Вычисление секанса | |
| Sin (x) | Синус угла | M=1/sin(ugol) | Вычисление косеканса | |
| Tan (x) | Тангенс угла | M=1/tan(ugol) | Вычисление котангенса | |
| Общие вычисления | Exp(x) | Возведение числа е в степень x | M=Exp(A) | Вычисление еA |
| Log (x) | Логарифм натуральный | M=Log(A) | Вычисление Ln(A),A>0 | |
| Sqr (x) | Квадратный корень числа | M=Sqr(A) | Вычисление 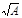 ,A>=0 ,A>=0
| |
| Вычисление абсолютного значения | Abs (x) | Абсолютное значение числа | M=Abs(A) | Вычисление |A| |
Выражения
Выражение – это комбинация операндов (констант, переменных, обращений к функциям), круглых скобок и знаков операций (операторов).
Операции определяют действия, которые надо выполнить над операндами. Например, в выражении (A + Sin(x) - 6) - A, Sin(x) и 6 – операнды; “+” и “-” – знаки операций (операторы) сложения и вычитания соответственно.
В простейшем случае выражение может состоять из одной переменной или константы.
Например:
Ø 123 (выражение – значение константы)
Ø Name (выражение – имя переменной или константы)
Круглые скобки в выражениях используются для управления порядком выполнения операций.
В зависимости от возвращаемого результата и используемых в выражении операторов различают числовые, строковые, логические выражения, выражения типа даты и объектные выражения.
Числовое выражение – это любое выражение, значением которого является число.
В числовых выражениях могут быть использованы только арифметические операции.
Например:
Ø Sin(x) + 3
Ø (2*x + b^5)/2
Ø (A + 1)\(x^2 + b) Mod (A + B)
Ø I Mod 2
Ø (Cos(x + 1) ^3) ^2
Пример 1.1. Вычислить значение выраженияy=sin ( 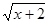 -1)
-1)
Фрагмент программы:
y = Sin(Sqr(x + 2) -1)
Пример 1.2. Вычислить значение выражения 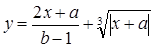
Фрагмент программы:
y= (2*x + a) / (b-1) + Abs(x + a) ^ (1/3)
Пример 1.3. Вычислить значение десятичного логарифма для выражения (x+1), т.е. y=lg(x+1)
Т.к. в VBA существует встроенная функция вычисления значения только натурального логарифма числового выражения, то для решения этой задачи потребуется формула приведения натурального логарифма к десятичному: Lg(x) =ln(x)/ln (10). Поэтому фрагмент программы будет выглядеть так:
y = log(x+1) / log (10)
Строковое выражение – любое выражение, значением которого является последовательность символов.
Операндами выражения могут быть функции, возвращающие строковые значения, строковые константы в явном представлении (литералы), строковые константы, строковые переменные.
В строковых выражениях могут быть использованы операции конкатенации.
Например:
Ø “1”& “ Мая”
Ø Fam & Im & Otch
Ø Kurs + Gruppa
Ø “Процент выполнения плана -” & Procent
Ø “Количество чисел, больших ” & Z & “ равно ” & K
Логическое выражение – любое выражение, возвращающее логическое значение. При составлении логического выражения могут быть использованы все виды операций.
Например:
Ø A>=B
Ø (x+1)<y
Ø (A(i)>x) And (A(i)<y)
Ø Name1=Name
Ø Sin(x+1)>(x+2)/3
Логическое выражение может быть простым или сложным.
Простые логические выражения могут содержать идентификаторы констант, переменных, обращений к функциям, числовые значения, арифметические и алгебраические выражения и обязательно какой-либо один из знаков отношения.
Например:
Ø x=2
Ø x+2>=3/(y+1)
Ø i<=N-i+1
Ø j<=M
Ø x>Z
Сложные логические выражения образуются объединением простых логических выражений с помощью логических операций.
Наиболее часто используются логические операции And (И) и Or (ИЛИ).
Например, если необходимо определить принадлежит ли значение переменной z промежутку [x;y], то используется сложное логическое выражение, состоящее из двух простых: z>=x и z<=y, - объединенных логической операцией And (И):
(z>=x) And (z<=y) или z>=x And z<=y
Если значение переменной z принадлежит заданному промежутку, то выражение принимает значение True, в противном случае значение выражения будет – False.

Если значение переменной z не должно принадлежать промежутку [x;y), то условие записывается с помощью следующего логического выражения
(z<x) Or (z>=y) или z<x Or z>=y
Если значение переменной z не принадлежит заданному промежутку, выражение принимает значение True, в противном случае значение выражения будет – False.
 Примеры сложных логических выражений:
Примеры сложных логических выражений:
Ø (i<=N) and (W=1)
Ø ((a>0) or (b<0)) and (c<>0)
Ø x>0 And (y>0 or z<0)
Ø (i>N) Or (i<M)
Ø c>3 or c>=10
Дата добавления: 2015-11-10; просмотров: 1532;
