Свойства плоской волны в однородной изотропной среде
Исследуем основные свойства плоской волны, распространяющейся в безграничной однородной изотропной среде. Она описывается уравнениями Даламбера (см. лекцию 2).
 (13)
(13)
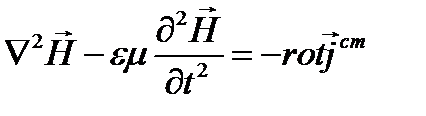 (14)
(14)
В комплексной форме эти уравнения записываются в виде:
 (8.15)
(8.15)
 (8.16)
(8.16)
Данные уравнения называются неоднородными уравнениями Гельмгольца. В случае, если источники, создающие волну, находятся за пределами рассматриваемой области уравнения (8.15), (8.16) (с учетом равенства  ) принимают вид
) принимают вид
 (8.17)
(8.17)
 (8.18)
(8.18)
Уравнения (8.17), (8.18) называются однородными уравнениями Гельмгольца. Поле рассматриваемой нами волны не зависит от координат х и у. Тогда уравнения (8.17) и (8.18) принимают вид
 (8.17)
(8.17)
 (8.18)
(8.18)
Решая уравнение для вектора 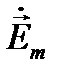 , получаем
, получаем
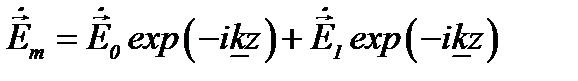 . (8.19)
. (8.19)
Для анализа формулы (8.19) необходимо в параметре  отделить действительную и мнимую части. Ограничимся рассмотрением случая, когда потери в среде обусловлены только ее проводимостью, т.е. будем считать, что
отделить действительную и мнимую части. Ограничимся рассмотрением случая, когда потери в среде обусловлены только ее проводимостью, т.е. будем считать, что 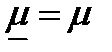 , а
, а  , где
, где  – тангенс угла электрических потерь. Полагая
– тангенс угла электрических потерь. Полагая  = Re
= Re  + i Im
+ i Im  , получаем Re
, получаем Re  + i Im
+ i Im  =
=  .
.
Возводя в квадрат обе части последнего равенства и разделяя затем вещественную и мнимую части, приходим к системе двух алгебраических уравнений относительно Re  и Im
и Im  :
:
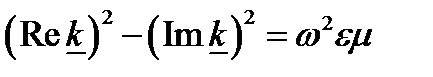 ;
; 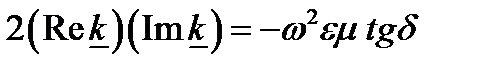 (8.20)
(8.20)
В результате получаем, что
 . (8.21)
. (8.21)
Так как ( 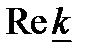 )2 не может быть отрицательной величиной, то в формуле (8.21) нужно выбрать знак"+". Вводя обозначение
)2 не может быть отрицательной величиной, то в формуле (8.21) нужно выбрать знак"+". Вводя обозначение
 , (8.22)
, (8.22)
получаем 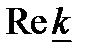 = ± β. Отметим, что β больше величины k в среде без потерь с теми же значениями ε и μ. Аналогично, обозначая
= ± β. Отметим, что β больше величины k в среде без потерь с теми же значениями ε и μ. Аналогично, обозначая
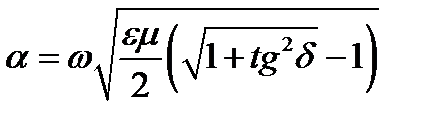 , (8.23)
, (8.23)
получаем Im  = ± α.
= ± α.
Из (8.20) видно, что Re  и Im
и Im  должны иметь разные знаки, т.е. возможны равенства
должны иметь разные знаки, т.е. возможны равенства  = β – iα и
= β – iα и  = –β + iα. Следовательно, входящие в (8.19) функции exp (-i
= –β + iα. Следовательно, входящие в (8.19) функции exp (-i  z) и exp (i
z) и exp (i  z) могут быть записаны одним из двух способов: 1) exp(–αz)exp(–iβz) и 2) exp(αz)exp(iβz). Рассмотрим волну 1). В момент t = t0 в точке z = z0 фаза напряженности электрического поля, соответствующего этой волне, равна ψ = ωt0 – βz0.
z) могут быть записаны одним из двух способов: 1) exp(–αz)exp(–iβz) и 2) exp(αz)exp(iβz). Рассмотрим волну 1). В момент t = t0 в точке z = z0 фаза напряженности электрического поля, соответствующего этой волне, равна ψ = ωt0 – βz0.

























Дата добавления: 2015-11-10; просмотров: 2288;
