Переход от сферической волны к плоской

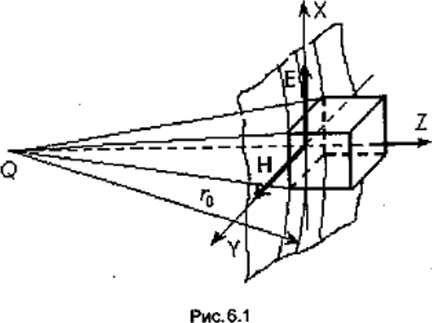
Рассмотрим электромагнитное поле, создаваемое ЭЭВ в дальней зоне в безграничной однородной изотропной среде без потерь. Предположим, что векторы Е и Н требуется знать только в области V, размеры которой малы по сравнению с расстоянием до источника (r₀). Введем декартову систему координат х у z, ось Z которой проведена вдоль радиус-вектора, соединяющего середину вибратора Q с точкой О, принятой за начало координат (рис. 6.1). В пределах области V можно пренебречь изменением амплитуд векторов 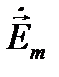и и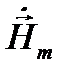, кроме того, считать, что их фазы зависят только от координаты z, т.е. считать, что sin Q/r = const, а ехр(–ikr)=ехр[–ik(r₀ + z)]. Вводя обозначение 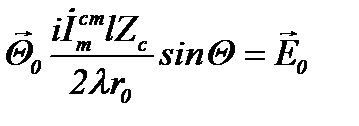, перепишем формулы для элементарного электрического вибратора в виде

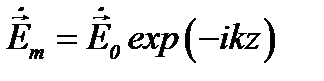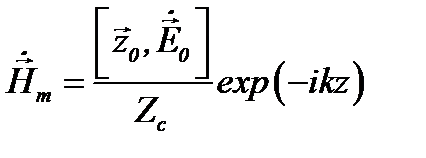, (8.14)

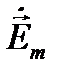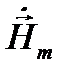В (8.14) учтено, что векторы и перпендикулярны друг другу и направлению распространения волны.

Поверхности равных фаз (ПРФ) определяются уравнением z = const, т.е. представляют собой плоскости, перпендикулярные оси Z. Волну. ПРФ которой образуют семейство параллельных плоскостей, называют плоской волной. Таким образом, сферическую волну, создаваемую ЭЭВ, в пределах области V можно рассматривать как плоскую волну.

Очевидно, аналогичный результат получится и в тех случаях, когда источником поля являются элементарный магнитный вибратор, элемент Гюйгенса, система таких излучателей и т.д.