Применение первого замечательного предела
Правило.Для раскрытия неопределенности вида 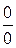 , содержащей тригонометрические выражения, используют первый замечательный предел:
, содержащей тригонометрические выражения, используют первый замечательный предел:
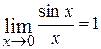 или
или 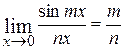 ,
,
где 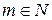 и
и 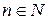 .
.
Примеры
Найти пределы функций:
1. 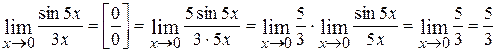 ;
;
2. 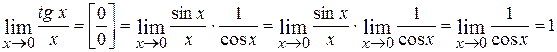 ;
;
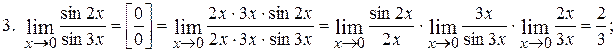
4. 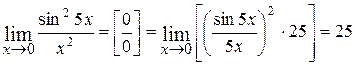 .
.
Применение эквивалентных бесконечно малых величин
Правило.Для раскрытия неопределенности вида 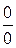 можно и числитель и знаменатель заменить величинами им эквивалентными (п.2.12).
можно и числитель и знаменатель заменить величинами им эквивалентными (п.2.12).
Примеры
Найти пределы функций:
1. 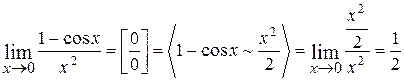 ;
;
2. 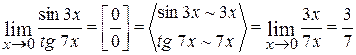 ;
;
3. 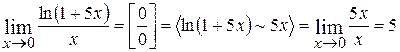 ;
;
4. 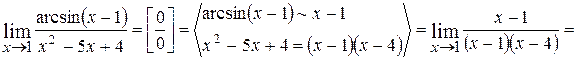
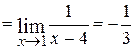 .
.
Неопределенности вида 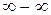 и
и 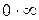
Если 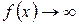 и
и 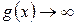 при
при 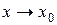
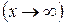 , то их разность
, то их разность 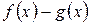 представляет собой неопределенность вида
представляет собой неопределенность вида 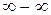 .
.
Если 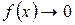 и
и 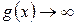 при
при 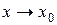
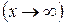 , то их произведение
, то их произведение 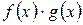 − это неопределенность вида
− это неопределенность вида 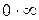 .
.
Правило.Неопределенности вида 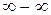 и
и 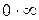 раскрываются путем их преобразования и сведения к неопределенностям вида
раскрываются путем их преобразования и сведения к неопределенностям вида 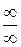 или
или 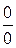 .
.
Примеры
Найти пределы функций:
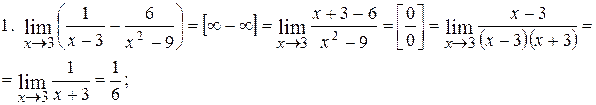
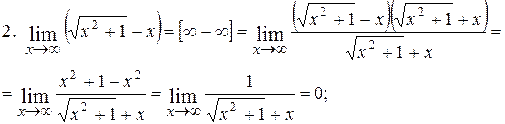
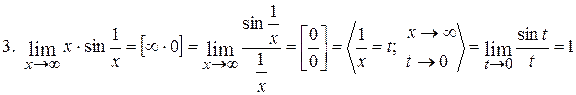 .
.
Неопределенности вида 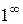 ,
, 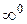 ,
, 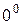
Пусть функция имеет вид:
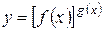 .
.
Если при 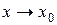
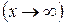 ,
, 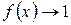 , а
, а 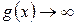 , то имеем неопределенность вида
, то имеем неопределенность вида 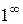 . Для раскрытия этой неопределенности применяют второй замечательный предел:
. Для раскрытия этой неопределенности применяют второй замечательный предел:
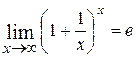 ;
; 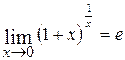 ;
;
или
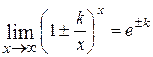 ;
; 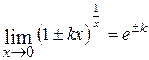 .
.
Примеры
Найти пределы функций:
1. 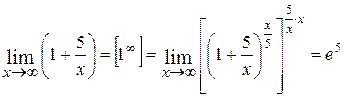 ;
;
2. 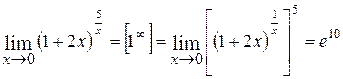 ;
;
3. 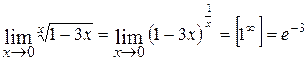 ;
;
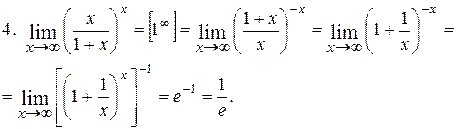
Если при 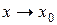
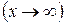 ,
,  , а
, а 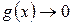 , то имеем неопределенность вида
, то имеем неопределенность вида 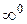 .
.
Если 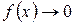 и
и 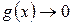 при
при 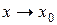
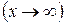 , то имеет место неопределенность
, то имеет место неопределенность 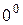 .
.
Для раскрытия неопределенностей вида 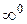 и
и 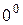 их преобразуют и сводят к неопределенности вида
их преобразуют и сводят к неопределенности вида 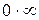 следующим образом:
следующим образом:
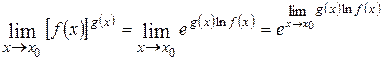 .
.
Примеры
Найти пределы функций:
1. 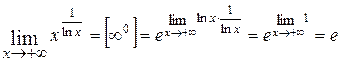 ;
;
2. 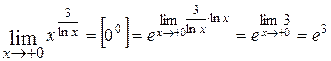 ;
;
В заключение отметим, что в дальнейшем будут рассмотрены более эффективные методы вычисления пределов функций, основанные на использовании понятия производной.
Упражнения
Односторонние пределы. Найти пределы:
1. 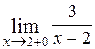 ; Ответ:
; Ответ: 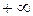 ;
;
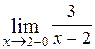 ; Ответ:
; Ответ: 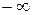 ;
;
2. 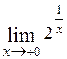 ; Ответь:
; Ответь: 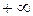 ;
;
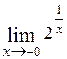 ; Ответ: 0.
; Ответ: 0.
Непосредственное вычисление пределов. Найти пределы:
3. 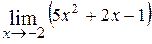 ; Ответ: 15;
; Ответ: 15;
4. 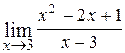 ; Ответ:
; Ответ: 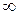 .
.
5. 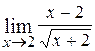 ; Ответ: 0.
; Ответ: 0.
Раскрытие неопределенности 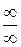 . Найти пределы:
. Найти пределы:
6. 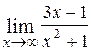 ; Ответ: 0;
; Ответ: 0;
7. 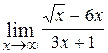 ; Ответ: -2;
; Ответ: -2;
8. 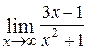 ; Ответ:
; Ответ: 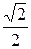 ;
;
9. 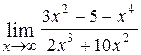 ; Ответ:
; Ответ: 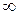 .
.
Раскрытие неопределенности 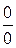 . Найти пределы:
. Найти пределы:
10. 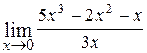 ; Ответ:
; Ответ: 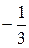 ;
;
11. 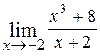 ; Ответ: -2;
; Ответ: -2;
12. 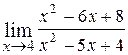 ; Ответ:
; Ответ: 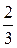 ;
;
13. 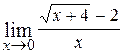 ; Ответ:
; Ответ: 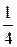 ;
;
14. 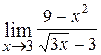 ; Ответ: -12;
; Ответ: -12;
15. 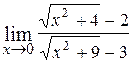 ; Ответ:
; Ответ: 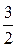 .
.
16. 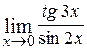 ; Ответ:
; Ответ: 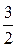 ;
;
17. 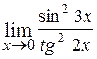 ; Ответ:
; Ответ: 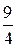 ;
;
18. 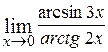 ; Ответ:
; Ответ: 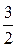 ;
;
19. 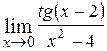 ; Ответ:
; Ответ: 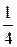 ;
;
20. 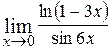 ; Ответ:
; Ответ: 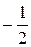 .
.
Раскрытие неопределенностей 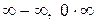 . Найти пределы:
. Найти пределы:
21. 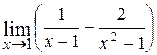 ; Ответ:
; Ответ: 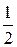 ;
;
22. 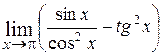 ; Ответ:
; Ответ: 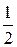 ;
;
23. 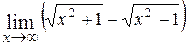 ; Ответ: 0;
; Ответ: 0;
24. 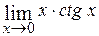 ; Ответ: 1.
; Ответ: 1.
Раскрытие неопределенности 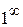 . Найти пределы:
. Найти пределы:
25. 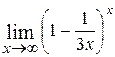 ; Ответ:
; Ответ: 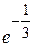 ;
;
26. 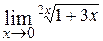 ; Ответ:
; Ответ: 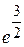 ;
;
27. 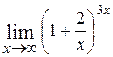 ; Ответ:
; Ответ: 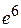 ;
;
28. 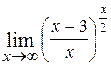 ; Ответ:
; Ответ: 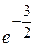 .
.
Дата добавления: 2015-11-10; просмотров: 950;
