Механическая вращательная подсистема

Фазовые переменные этой подсистемы — моменты сил М и угловые скорости ω — соответственно, аналоги токов и напряжений. Запишем уравнения трех типов простейших элементов.

1. Уравнение вязкого трения вращения М = ω/R_вр, где R_вр – 1/k — аналог электрического сопротивления; k — коэффициент трения вращения.

2. Основное уравнение динамики вращательного движения М = J(dω/dt), где J — аналог электрической емкости (момент инерции элемента).

3. Уравнение кручения бруса с круглым поперечным сечением М = GJ_pθ, где М — крутящий момент; G — модуль сдвига; J_p — полярный момент инерции сечения; θ = d 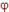/dl — относительный угол закручивания.

Рассмотрим брус конечной длины, тогда θ = 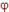/l, где 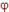— угол закручивания; l — длина бруса. Продифференцируем обе части уравнения по времени, т. е. dM/dt – (GJ_р/l)(d 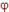/dt), или если учесть, что (d 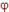/dt) = ω и L_вр = l/(GJ_p), то ω = L_вр (dM/dt), где L_вр — аналог электрической индуктивности (вращательная гибкость).

Аналогичное компонентное уравнение можно получить для спиральной пружины, М = с 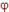, где с — жесткость пружины. Продифференцировав обе части уравнения по времени, получим ω = L_вp(dM/dt); L_вp = l/c.

13. Лекция: Математические модели (ММ) на различных иерархических уровнях //

//