Блок-схема метода деления отрезка пополам и числовой пример

Сужение отрезка производится путем замены границ а или b на текущее значение корня х. При этом значение f(a) вычисляется лишь один раз, так как нам нужен только знак функции f(x) на левой границе, а он в процессе итераций не меняется.

Метод деления отрезка пополам довольно медленный, однако он всегда сходится, т.е. при его использовании решение получается всегда, причем с заданной точностью.

На рис. 3.2 представлена блок-схема метода половинного деления.

Пример. Методом деления отрезка пополам найти хотя бы один корень уравнения с погрешностью e = 0,005.

Представим уравнение к виду 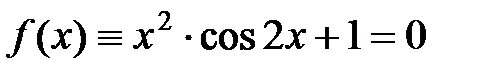. Для определения [a, b], на котором имеется хотя бы один корень, выполним табулирование

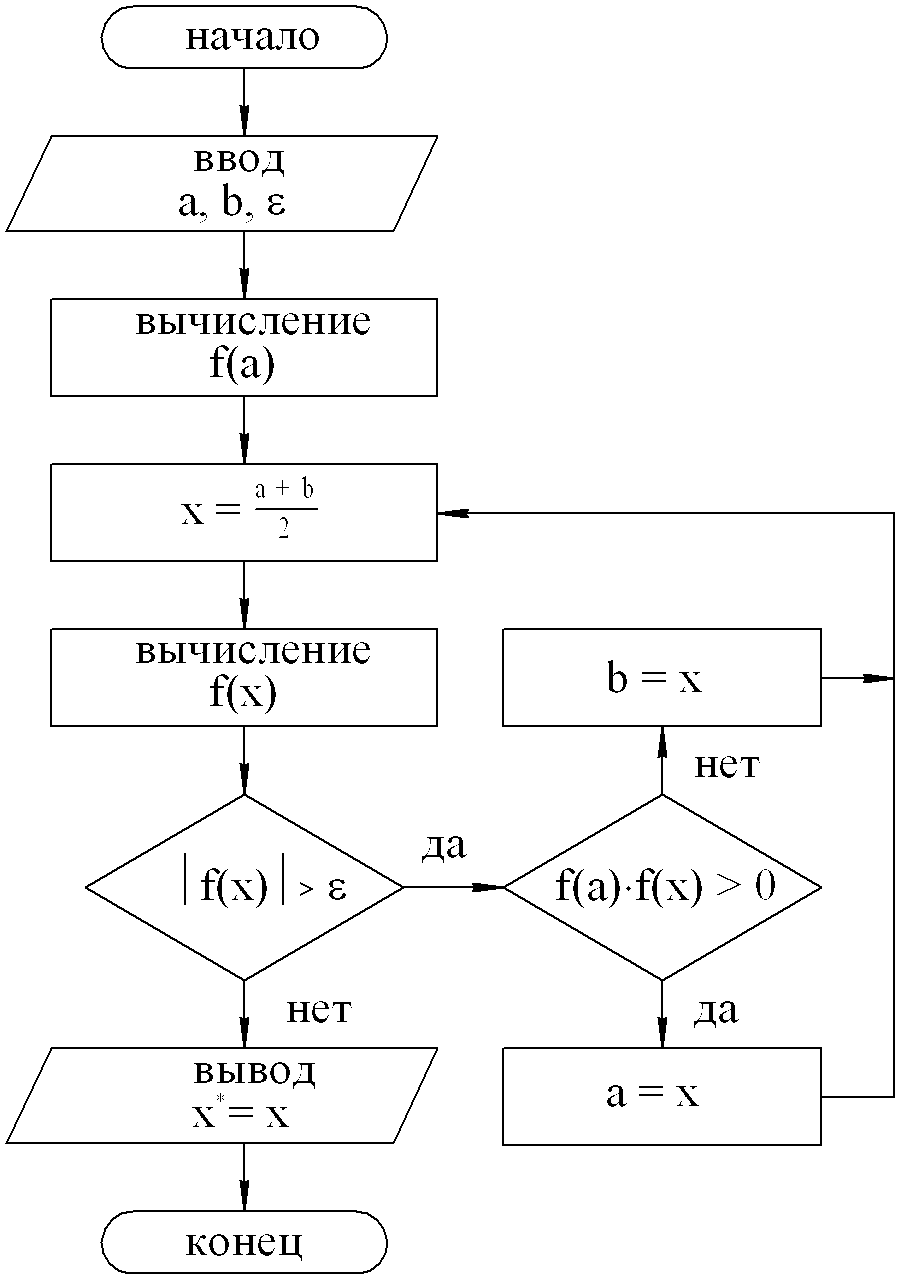
Рис. 3.2. Блок-схема метода половинного деления

функции f(x). Пусть уравнение описывает скорость изменения подвижного узла механизма в зависимости от угла поворота кривошипа: f(x) – скорость в м/с; х –

угол в радианах, х = 0…2π (0…6,28). Результаты табулирования функции представлены в табл. 3.1.

Можно принять а=0,9; b=1,2 , т.к. f(0,9)×f(1,2) < 0. Уточним значение а, т.к. видно, что корень х^* лежит ближе к b (f(b) ближе к 0).

Таблица 3.1

Результаты табулирования функции f(x)

Пусть а=1,1; f(1,1)=0,29. Окончательно: а=1,1, b=1,2, f(1,1)×f(1,2) < 0.

Значит корень .

Уточнение а позволяет снизить число итераций. Последовательно имеем:

1) f (1,1) = 0,289;

2) f (1,2) = -0,062;

3) f (x) = f [(a+b)/2] = f (1,15) = 0,119; n=1

4) f [(1,15+1,2)/2] = f (1,175) = 0,030; n=2

5) f [(1,175+1,2)/2] = f (1,1875) = -0,016; n=3

6) f [(1,175+1,1875)/2] = f (1,18125) = 0,007; n=4

7) f [(1,1875+1,18125)/2] = f (1,184375) =- 0,004; n=5

½ f (x)½< 0,005; (e = 0,005).

Корень х = х^* = 1,184375.