Метод деления отрезка пополам (метод половинного деления)
Позволяет решать нелинейные трансцендентные, а также алгебраические уравнения. Это один из простейших численных методов. На первом шаге необходимо найти отрезок [a; b], в котором расположено искомое значения корня х = х*; a < x*< b; 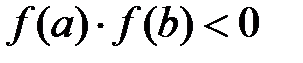 .
.
В качестве начального приближения корня х0 принимаем середину отрезка [a, b], т.е. х0 = (a+b)/2. Далее определяем значение функции f(x) в точках a, x0, b; т.е. на концах отрезков [a, x0] и [x0, b]. Тот из них, на концах которого f(x) имеет разные знаки, содержит искомый корень. Поэтому его принимают в качестве нового отрезка. Вторую половину отрезка [a, b], на которой знак f(x) не меняется, отбрасываем. В качестве первой итерации корня принимаем середину нового отрезка и т.д. Таким образом, после каждой итерации отрезок, на котором расположен корень, уменьшается вдвое. Т.е. после nитераций он сокращается в 2nраз.
Пусть для определенности f(a) < 0, f(b) > 0 (рис. 3.1).
Начальное приближение корня х0 = (a+b)/2. Т.к. f(x0) < 0, то x0 < x* < b и рассмотрим только [x0, b]. Следующее приближение: х1 = (х0+b)/2. Сейчас отбрасываем отрезок [x1, b], т.к. f(x1) > 0 и f(b) > 0. Т.е. x0 < x*< x1. Аналогично находим другие приближения: x2 = (x0+x1) /2 и т.д.

Рис. 3.1. Графическая иллюстрация метода половинного деления
Итерационный процесс продолжается до тех пор, пока значение функции
f(x) после n-ой итерации не станет меньшим по модулю некоторого малого заданного числа e, т.е. 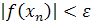 .
.
Дата добавления: 2015-08-21; просмотров: 2162;
