Связями
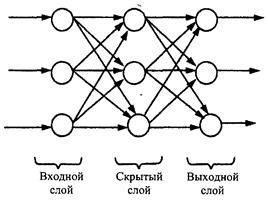
Рис.6.8.Трёхслойная сеть с прямыми связями
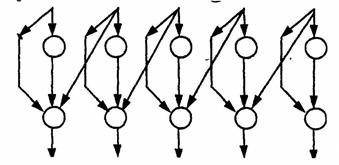Рис.6.9.Нейронная сеть с перекрёстными связями
На рис.6.6 представлена однослойная сеть с ортогональными связями между нейронами.
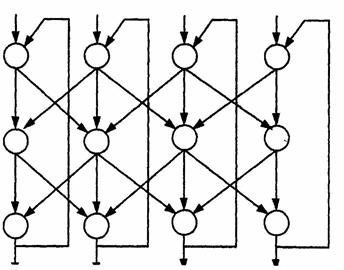
Рис.6.10.Нейронная сеть с обратными связями
В это сети любой из нейронов может быть выходным или входным. На рис.6.7 представлена сеть с прямыми связями. Характерной особенностью такой сети является равенство число входов, выходов и нейронов в каждом из двух слоёв сети, а также наличие так называемых латеральных связей между нейронами 1-го и 2-го слоёв. На рис.6.8 показана многослойная, в частности трёхслойная сеть. В общем случае скрытых слоёв может быть несколько. В многослойных сетях, как правило, нейроны одного слоя имеют функцию активации одного типа. На рис.6.9 представлена нейронная сеть с перекрёстными связями. Число связей может быть и больше, чем показано на рисунке. На рис.6.10 иллюстрирует топологию сети с обратными связями. Обратные связи могут быть как с внешнего слоя на входной, так и с внутренних (скрытых) слоёв на входной.
Следует отметить, что при конструировании сети в качестве исходных данных разработчик имеет:
- размерность вектора входного сигнала (-ов);
- размерность вектора выходного сигнала (-ов);
- формулировку решаемой задачи;
- заданную точность решения задачи.
При этом разработчик должен выбрать:
- тип топологии сети;
- общее число нейронов в сети и по слоям;
- функции активации нейронов;
- способ задания коэффициентов синоптической связи;
- метод доказательства работоспособности новой связи.
В работе А.И. Галушкина разработана методология синтеза многослойных НС как адаптивных систем определенного вида. Общая задача синтеза топология многослойных НС в настоящее время не решена – предлагаются лишь некоторые частные методики. В обычной практике построения нейронных сетей следуют следующим рекомендациям:
- число слоёв в выходном слое равно числу классов;
- все входные сигналы подаются всем нейронам;
- вариант топологии сети определяется на основе априорных знаний о задаче;
- для улучшения характеристик сети используются комбинированные многослойные сети, каждый слой которой представляется различной топологией и обучается по определённому алгоритму.
Классификация сложных систем, а нейронные сети являются таковыми, всегда проводится по определённому признаку. Ранее была приведена классификация нейронных сетей по топологии. Ещё раньше было упомянуто, что нейрокомпьютеры, а следовательно, и нейронные сети могут быть аналоговыми и цифровыми. Кроме этого, нейронные сети классифицируются по способу решения задач, выделяя формируемые сети, сети с формируемой матрицей связи и обучаемые.
Формируемые сети – это сети класса проектируются для формализуемых задач, имеющих чётко сформулированный в нейросетевом базисе алгоритм решения конкретной задачи.
Сети с формируемой матрицей связи. Сети этого класса применяются для трудноформализуемых задач. Как правило, эти сети имеют одинаковую структуру и различаются лишь матрицей связи. Примером таких сетей является сеть Хопфилда. Достоинством таких сетей является их наглядность в работе.
Обучаемые сети – это обучаемые сети используют для решения неформализуемых задач. В процессе обучения сети автоматически изменяются такие её параметры, как коэффициенты синоптической связи, а в некоторых случаях и топология. Серьёзным препятствием в широком применении нейрокомпьютеров все ещё остаётся большое время обучении сети. Поэтому выбор и разработка алгоритма обучения является ключевой задачей разработчика нейронных систем. Для сетей с формулируемой матрицей связи и обучаемых характерным является процедура обучения.
Обучение нейронных сетей. В процессе функционирования нейронная сеть формирует выходной сигнал Y в соответствии с входным сигналом Х, реализуя некоторую функцию g: Y=g(X). Если архитектура сети задана, то вид функции g определяется значениями весов связей (синаптических весов) между нейронами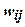 
и смещений нейронов в сети (b). Обозначим буквой G множество всех возможных функций g, соответствующих заданной архитектуре сети. Пусть решение некоторой задачи – функция F: Y=F(X), заданная парами входных и выходных данных 
, 
,…, 
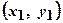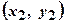, для которых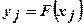 
, 
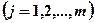, и пусть 
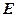- функция ошибки, показывающая для каждой из функций g степень близости к F.
Решить поставленную задачу с помощью нейронной сети заданной архитектуры – это значит построить (синтезировать) функцию, подобрав параметры нейронов (синаптические веса и смещения) таким образом, чтобы функционал качества являлся оптимальным для всех пар . Задача обучения определяется совокупностью пяти элементов: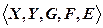 
, где 
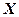и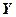 
- вход и выход нейронной сети соответственно; 
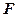- функция, определяющая желаемый результат обучения ( в задаче обучения по примерам функция 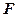задаётся парами входных и выходных данных: 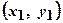, ,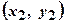…, , для 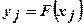, , 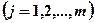при этом архитектура связей нейронной сети считается заданной до начала обучения и определяет множество функций 
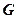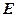); - функция ошибки, показывающая для каждого входного вектора степень близости реализуемой функции к .
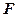Обучение состоит в поиске (синтезе) функции 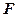, оптимальной по 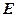. Обучение – это итерационная процедура, причём на каждой итерации происходит уменьшение значения функции ошибки 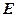до заранее заданной величины. В общем случае такая задача при ограниченном наборе данных имеет бесконечное множество решений.
Таким образом, результатом обучения нейронной сети должно стать отображение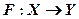 
, такое, чтобы для каждого возможного входного сигнала формировался правильный выходной сигнал Y; если используется единственный выход сети, то Y является скаляром. Отображение задаётся конечным набором пар (вход – известный выход). Число таких пар (обучающих примеров) существенно меньше общего числа возможных сочетаний значений входных и выходных сигналов. Совокупность всех обучающих примеров называется обучающей выборкой. В результате построения отображения необходимо добиться того, чтобы обеспечивалось формирование правильных выходных сигналов в соответствии:
1) со всеми примерами обучающей выборки;
2) со всеми возможными входными сигналами, которые не вошли в обучающую выбору.
Второе требование связано с необходимостью реализации процедуры предсказания значения выхода в зависимости от входного сигнала. Иными словами, необходимого построить такое при подаче входного вектора X на выходе сети определяло бы значение одного или нескольких правильных выходных сигналов. Решение этой задачи в значительной степени зависит от качества обучающей выборки в общем виде в настоящее время не решена и требует дальнейшей проработки.
Задача построения отображения 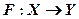опирается на известную теорему А.Н. Колмогорова о предоставлении непрерывных функций нескольких переменных в виде суперпозиции непрерывных функций одного переменного и операции сложения, примененную затем Хехт – Нильсеном к нейронным сетям. Основной результат этого обобщения – возможность реализации произвольной функции 
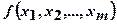нейронной сетью. Уже доказано, что для любого множества пар ( 
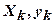), где 
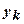-скаляр, существует двухслойная однородная (с одинаковыми функциями активации каждого нейрона) нейронная сеть первого порядка с последовательными связями и с конечным числом нейронов, которая выполняет отображение 
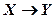, выдавая на каждый входной сигнал 
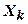правильный выходной сигнал 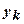. Таким образом, отображение 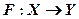может быть построено с помощью двухслойной нейронной сети.
Однако теорема Хехт - Нильсена не конструктивна, это лишь теорема существования, в ней не заложена методика определения числа нейронов в сети для конкретной обучающей выборки. Для первоначальной оценки числа нейронов в скрытых слоях однородных нейронных сетей часто используется формула для оценки необходимого числа синаптических весов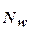 
в многослойной сети:
,
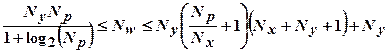где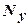 
- размерность выходного сигнала; 
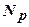- число элементов обучающей выборки; 
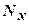- размерность входного сигнала.
Оценив 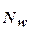можно рассчитать число нейронов в скрытых слоях.
Контрольные вопросы к лекции 6
Дата добавления: 2015-08-21; просмотров: 1269;