Основные алгоритмы сжатия
Алгоритмы архивации без потерь
Алгоритм RLE
Первый вариант алгоритма
Данный алгоритм необычайно прост в реализации. Групповое кодирование — от английского Run Length Encoding (RLE) — один из самых старых и самых простых алгоритмов архивации графики. Изображение в нем (как и в нескольких алгоритмах, описанных ниже) вытягивается в цепочку байт по строкам растра. Само сжатие в RLE происходитза счет того, что в исходном изображении встречаются цепочки одинаковых байт. Замена их на пары <счетчик повторений, значение> уменьшает збыточность данных.
В данном алгоритме признаком счетчика (counter) служат единицы в двух верхних битах считанного файла:
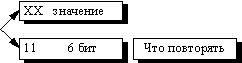 Соответственно оставшиеся 6 бит расходуются на счетчик, который может принимать значения от 1 до 64. Строку из 64 повторяющихся байтов мы превращаем в два байта, т.е. сожмем в 32 раза.
Упражнение: Составьте алгоритм компрессии для первого варианта алгоритма RLE.
Алгоритм рассчитан на деловую графику — изображения с большими областями повторяющегося цвета. Ситуация, когда файл увеличивается, для этого простого алгоритма не так уж редка. Ее можно легко получить, применяя групповое кодирование к обработанным цветным фотографиям. Для того, чтобы увеличить изображение в два раза, его надо применить к изображению, в котором значения всех пикселов больше двоичного 11000000 и подряд попарно не повторяются.
Вопрос к экзамену: Предложите два-три примера “плохих” изображений для алгоритма RLE. Объясните, почему размер сжатого файла больше размера исходного файла.
.
Характеристики алгоритма RLE:
Коэффициенты компрессии:Первый вариант: 32, 2, 0,5. Второй вариант: 64, 3, 128/129.(Лучший, средний, худший коэффициенты)
Класс изображений: Ориентирован алгоритм на изображения с небольшим количеством цветов: деловую и научную графику.
Симметричность: Примерно единица.
Характерные особенности: К положительным сторонам алгоритма, пожалуй, можно отнести только то, что он не требует дополнительной памяти при архивации и разархивации, а также быстро работает. Интересная особенность группового кодирования состоит в том, что степень архивации для некоторых изображений может быть существенно повышена всего лишь за счет изменения порядка цветов в палитре изображения.
Соответственно оставшиеся 6 бит расходуются на счетчик, который может принимать значения от 1 до 64. Строку из 64 повторяющихся байтов мы превращаем в два байта, т.е. сожмем в 32 раза.
Упражнение: Составьте алгоритм компрессии для первого варианта алгоритма RLE.
Алгоритм рассчитан на деловую графику — изображения с большими областями повторяющегося цвета. Ситуация, когда файл увеличивается, для этого простого алгоритма не так уж редка. Ее можно легко получить, применяя групповое кодирование к обработанным цветным фотографиям. Для того, чтобы увеличить изображение в два раза, его надо применить к изображению, в котором значения всех пикселов больше двоичного 11000000 и подряд попарно не повторяются.
Вопрос к экзамену: Предложите два-три примера “плохих” изображений для алгоритма RLE. Объясните, почему размер сжатого файла больше размера исходного файла.
.
Характеристики алгоритма RLE:
Коэффициенты компрессии:Первый вариант: 32, 2, 0,5. Второй вариант: 64, 3, 128/129.(Лучший, средний, худший коэффициенты)
Класс изображений: Ориентирован алгоритм на изображения с небольшим количеством цветов: деловую и научную графику.
Симметричность: Примерно единица.
Характерные особенности: К положительным сторонам алгоритма, пожалуй, можно отнести только то, что он не требует дополнительной памяти при архивации и разархивации, а также быстро работает. Интересная особенность группового кодирования состоит в том, что степень архивации для некоторых изображений может быть существенно повышена всего лишь за счет изменения порядка цветов в палитре изображения.
|
Алгоритм LZW
Название алгоритм получил по первым буквам фамилий его разработчиков — Lempel, Ziv и Welch. Сжатие в нем, в отличие от RLE, осуществляется уже за счет одинаковых цепочек байт.
Алгоритм LZ
Существует довольно большое семейство LZ-подобных алгоритмов, различающихся, например, методом поиска повторяющихся цепочек. Один из достаточно простых вариантов этого алгоритма, например, предполагает, что во входном потоке идет либо пара <счетчик, смещение относительно текущей позиции>, либо просто <счетчик> “пропускаемых” байт и сами значения байтов (как во втором варианте алгоритма RLE). При разархивации для пары <счетчик, смещение> копируются <счетчик> байт из выходного массива, полученного в результате разархивации, на <смещение> байт раньше, а <счетчик> (т.е. число равное счетчику) значений “пропускаемых” байт просто копируются в выходной массив из входного потока. Данный алгоритм является несимметричным по времени, поскольку требует полного перебора буфера при поиске одинаковых подстрок. В результате нам сложно задать большой буфер из-за резкого возрастания времени компрессии. Однако потенциально построение алгоритма, в котором на <счетчик> и на <смещение> будет выделено по 2 байта (старший бит старшего байта счетчика — признак повтора строки / копирования потока), даст нам возможность сжимать все повторяющиеся подстроки размером до 32Кб в буфере размером 64Кб.
 При этом мы получим увеличение размера файла в худшем случае на 32770/32768 (в двух байтах записано, что нужно переписать в выходной поток следующие 215 байт), что совсем неплохо. Максимальный коэффициент сжатия составит в пределе 8192 раза. В пределе, поскольку максимальное сжатие мы получаем, превращая 32Кб буфера в 4 байта, а буфер такого размера мы накопим не сразу. Однако, минимальная подстрока, для которой нам выгодно проводить сжатие, должна состоять в общем случае минимум из 5 байт, что и определяет малую ценность данного алгоритма. К достоинствам LZ можно отнести чрезвычайную простоту алгоритма декомпрессии.
Упражнение: Предложите другой вариант алгоритма LZ, в котором на пару <счетчик, смещение> будет выделено 3 байта, и подсчитайте основные характеристики своего алгоритма.
Алгоритм LZW
Рассматриваемый нами ниже вариант алгоритма будет использовать дерево для представления и хранения цепочек. Очевидно, что это достаточно сильное ограничение на вид цепочек, и далеко не все одинаковые подцепочки в нашем изображении будут использованы при сжатии. Однако в предлагаемом алгоритме выгодно сжимать даже цепочки, состоящие из 2 байт.
Процесс сжатия выглядит достаточно просто. Мы считываем последовательно символы входного потока и проверяем, есть ли в созданной нами таблице строк такая строка. Если строка есть, то мы считываем следующий символ, а если строки нет, то мы заносим в поток код для предыдущей найденной строки, заносим строку в таблицу и начинаем поиск снова.
Характеристики алгоритмаLZW:
Коэффициенты компрессии: Примерно1000, 4, 5/7 (Лучший, средний, худший коэффициенты). Сжатие в 1000 раз достигается только на одноцветных изображениях размером кратным примерно 7 Мб.
Класс изображений: Ориентирован LZW на 8-битные изображения, построенные на компьютере. Сжимает за счет одинаковых подцепочек в потоке.
Симметричность: Почти симметричен, при условии оптимальной реализации операции поиска строки в таблице.
Характерные особенности: Ситуация, когда алгоритм увеличивает изображение, встречается крайне редко. LZW универсален — именно его варианты используются в обычных архиваторах.
При этом мы получим увеличение размера файла в худшем случае на 32770/32768 (в двух байтах записано, что нужно переписать в выходной поток следующие 215 байт), что совсем неплохо. Максимальный коэффициент сжатия составит в пределе 8192 раза. В пределе, поскольку максимальное сжатие мы получаем, превращая 32Кб буфера в 4 байта, а буфер такого размера мы накопим не сразу. Однако, минимальная подстрока, для которой нам выгодно проводить сжатие, должна состоять в общем случае минимум из 5 байт, что и определяет малую ценность данного алгоритма. К достоинствам LZ можно отнести чрезвычайную простоту алгоритма декомпрессии.
Упражнение: Предложите другой вариант алгоритма LZ, в котором на пару <счетчик, смещение> будет выделено 3 байта, и подсчитайте основные характеристики своего алгоритма.
Алгоритм LZW
Рассматриваемый нами ниже вариант алгоритма будет использовать дерево для представления и хранения цепочек. Очевидно, что это достаточно сильное ограничение на вид цепочек, и далеко не все одинаковые подцепочки в нашем изображении будут использованы при сжатии. Однако в предлагаемом алгоритме выгодно сжимать даже цепочки, состоящие из 2 байт.
Процесс сжатия выглядит достаточно просто. Мы считываем последовательно символы входного потока и проверяем, есть ли в созданной нами таблице строк такая строка. Если строка есть, то мы считываем следующий символ, а если строки нет, то мы заносим в поток код для предыдущей найденной строки, заносим строку в таблицу и начинаем поиск снова.
Характеристики алгоритмаLZW:
Коэффициенты компрессии: Примерно1000, 4, 5/7 (Лучший, средний, худший коэффициенты). Сжатие в 1000 раз достигается только на одноцветных изображениях размером кратным примерно 7 Мб.
Класс изображений: Ориентирован LZW на 8-битные изображения, построенные на компьютере. Сжимает за счет одинаковых подцепочек в потоке.
Симметричность: Почти симметричен, при условии оптимальной реализации операции поиска строки в таблице.
Характерные особенности: Ситуация, когда алгоритм увеличивает изображение, встречается крайне редко. LZW универсален — именно его варианты используются в обычных архиваторах.
|
Алгоритм Хаффмана
Классический алгоритм Хаффмана
Один из классических алгоритмов, известных с 60-х годов. Использует только частоту появления одинаковых байт в изображении. Сопоставляет символам входного потока, которые встречаются большее число раз, цепочку бит меньшей длины. И, напротив, встречающимся редко — цепочку большей длины. Для сбора статистики требует двух проходов по изображению.
Для начала введем несколько определений.
Определение.Пусть задан алфавит Y ={a1, ..., ar}, состоящий из конечного числа букв. Конечную последовательность символов из Y
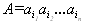 будем называть словом в алфавите Y , а число n — длиной слова A. Длина слова обозначается как l(A).
Пусть задан алфавит W , W ={b1, ..., bq}. Через B обозначим слово в алфавите W и через S(W ) — множество всех непустых слов в алфавите W .
Пусть S=S(Y ) — множество всех непустых слов в алфавите Y , и S' — некоторое подмножество множества S. Пусть также задано отображение F, которое каждому слову A, A? S(Y ), ставит в соответствие слово
B=F(A), B? S(W ).
Слово В будем назвать кодом сообщения A, а переход от слова A к его коду — кодированием.
Определение.Рассмотрим соответствие между буквами алфавита Y и некоторыми словами алфавита W :
a1 — B1, a2 — B2, . . . ar — Br
Это соответствие называют схемой и обозначают через S . Оно определяет кодирование следующим образом: каждому слову
будем называть словом в алфавите Y , а число n — длиной слова A. Длина слова обозначается как l(A).
Пусть задан алфавит W , W ={b1, ..., bq}. Через B обозначим слово в алфавите W и через S(W ) — множество всех непустых слов в алфавите W .
Пусть S=S(Y ) — множество всех непустых слов в алфавите Y , и S' — некоторое подмножество множества S. Пусть также задано отображение F, которое каждому слову A, A? S(Y ), ставит в соответствие слово
B=F(A), B? S(W ).
Слово В будем назвать кодом сообщения A, а переход от слова A к его коду — кодированием.
Определение.Рассмотрим соответствие между буквами алфавита Y и некоторыми словами алфавита W :
a1 — B1, a2 — B2, . . . ar — Br
Это соответствие называют схемой и обозначают через S . Оно определяет кодирование следующим образом: каждому слову 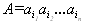 из S'(W )=S(W ) ставится в соответствие слово из S'(W )=S(W ) ставится в соответствие слово 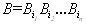 , называемое кодом слова A. Слова B1 ... Br называются элементарными кодами. Данный вид кодирования называют алфавитным кодированием.
Определение. Пусть слово В имеет вид
B=B' B"
Тогда слово B'называется началом или префиксом слова B, а B" — концом слова B. При этом пустое слово L и само слово B считаются началами и концами слова B.
Определение. Схема Sобладает свойством префикса, если для любыхiи j(1?i, j? r, i? j) слово Bi не является префиксом слова Bj.
Теорема 1. Если схема Sобладает свойством префикса, то алфавитное кодирование будет взаимно однозначным.
Предположим, что задан алфавит Y ={a1,..., ar} (r>1) и набор вероятностей p1, . . . , pr , называемое кодом слова A. Слова B1 ... Br называются элементарными кодами. Данный вид кодирования называют алфавитным кодированием.
Определение. Пусть слово В имеет вид
B=B' B"
Тогда слово B'называется началом или префиксом слова B, а B" — концом слова B. При этом пустое слово L и само слово B считаются началами и концами слова B.
Определение. Схема Sобладает свойством префикса, если для любыхiи j(1?i, j? r, i? j) слово Bi не является префиксом слова Bj.
Теорема 1. Если схема Sобладает свойством префикса, то алфавитное кодирование будет взаимно однозначным.
Предположим, что задан алфавит Y ={a1,..., ar} (r>1) и набор вероятностей p1, . . . , pr 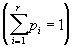 появления символов a1,..., ar. Пусть, далее, задан алфавит W , W ={b1, ..., bq} (q>1). Тогда можно построить целый ряд схем S алфавитного кодирования
a1 — B1, . . . ar — Br
обладающих свойством взаимной однозначности.
Для каждой схемы можно ввести среднюю длину lср, определяемую как математическое ожидание длины элементарного кода: появления символов a1,..., ar. Пусть, далее, задан алфавит W , W ={b1, ..., bq} (q>1). Тогда можно построить целый ряд схем S алфавитного кодирования
a1 — B1, . . . ar — Br
обладающих свойством взаимной однозначности.
Для каждой схемы можно ввести среднюю длину lср, определяемую как математическое ожидание длины элементарного кода:
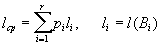 — длины слов.
Длина lср показывает, во сколько раз увеличивается средняя длина слова при кодировании со схемой S .
Можно показать, что lср достигает величины своего минимума l* на некоторой Sи определена как — длины слов.
Длина lср показывает, во сколько раз увеличивается средняя длина слова при кодировании со схемой S .
Можно показать, что lср достигает величины своего минимума l* на некоторой Sи определена как
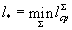 Определение. Коды, определяемые схемой S сlср= l*, называются кодами с минимальной избыточностью, или кодами Хаффмана.
Коды с минимальной избыточностью дают в среднем минимальное увеличение длин слов при соответствующем кодировании.
В нашем случае, алфавит Y ={a1,..., ar} задает символы входного потока, а алфавит W ={0,1}, т.е. состоит всего из нуля и единицы.
Алгоритм построения схемы S можно представить следующим образом:
Шаг 1. Упорядочиваем все буквы входного алфавита в порядке убывания вероятности. Считаем все соответствующие слова Bi из алфавита W ={0,1} пустыми.
Шаг 2. Объединяем два символа air-1 и air с наименьшими вероятностями pi r-1 и pi r в псевдосимвол a'{air-1 air} c вероятностью pir-1+pir. Дописываем 0 в начало слова Bir-1 (Bir-1=0Bir-1), и 1 в начало слова Bir (Bir=1Bir).
Шаг 3. Удаляем из списка упорядоченных символов air-1 и air, заносим туда псевдосимвол a'{air-1air}. Проводим шаг 2, добавляя при необходимости 1 или ноль для всех слов Bi, соответствующих псевдосимволам, до тех пор, пока в списке не останется 1 псевдосимвол.
Пример: Пусть у нас есть 4 буквы в алфавите Y ={a1,..., a4} (r=4), p1=0.5, p2=0.24, p3=0.15, p4=0.11
Определение. Коды, определяемые схемой S сlср= l*, называются кодами с минимальной избыточностью, или кодами Хаффмана.
Коды с минимальной избыточностью дают в среднем минимальное увеличение длин слов при соответствующем кодировании.
В нашем случае, алфавит Y ={a1,..., ar} задает символы входного потока, а алфавит W ={0,1}, т.е. состоит всего из нуля и единицы.
Алгоритм построения схемы S можно представить следующим образом:
Шаг 1. Упорядочиваем все буквы входного алфавита в порядке убывания вероятности. Считаем все соответствующие слова Bi из алфавита W ={0,1} пустыми.
Шаг 2. Объединяем два символа air-1 и air с наименьшими вероятностями pi r-1 и pi r в псевдосимвол a'{air-1 air} c вероятностью pir-1+pir. Дописываем 0 в начало слова Bir-1 (Bir-1=0Bir-1), и 1 в начало слова Bir (Bir=1Bir).
Шаг 3. Удаляем из списка упорядоченных символов air-1 и air, заносим туда псевдосимвол a'{air-1air}. Проводим шаг 2, добавляя при необходимости 1 или ноль для всех слов Bi, соответствующих псевдосимволам, до тех пор, пока в списке не останется 1 псевдосимвол.
Пример: Пусть у нас есть 4 буквы в алфавите Y ={a1,..., a4} (r=4), p1=0.5, p2=0.24, p3=0.15, p4=0.11 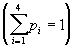 . Тогда процесс построения схемы можно представить так: . Тогда процесс построения схемы можно представить так:
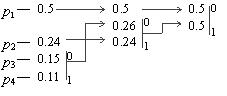 Производя действия, соответствующие 2-му шагу, мы получаем псевдосимвол с вероятностью 0.26 (и приписываем 0 и 1 соответствующим словам). Повторяя же эти действия для измененного списка, мы получаем псевдосимвол с вероятностью 0.5. И, наконец, на последнем этапе мы получаем суммарную вероятность 1.
Для того, чтобы восстановить кодирующие слова, нам надо пройти по стрелкам от начальных символов к концу получившегося бинарного дерева. Так, для символа с вероятностью p4, получим B4=101, для p3 получим B3=100, для p2 получим B2=11, для p1 получим B1=0. Что означает схему:
a1 — 0, a2 — 11 a3 — 100 a4 — 101
Эта схема представляет собой префиксный код, являющийся кодом Хаффмана. Самый часто встречающийся в потоке символ a1 мы будем кодировать самым коротким словом 0, а самый редко встречающийся a4 длинным словом 101.
Для последовательности из 100 символов, в которой символ a1 встретится 50 раз, символ a2 — 24 раза, символ a3 — 15 раз, а символ a4 — 11 раз, данный код позволит получить последовательность из 176 бит (
Производя действия, соответствующие 2-му шагу, мы получаем псевдосимвол с вероятностью 0.26 (и приписываем 0 и 1 соответствующим словам). Повторяя же эти действия для измененного списка, мы получаем псевдосимвол с вероятностью 0.5. И, наконец, на последнем этапе мы получаем суммарную вероятность 1.
Для того, чтобы восстановить кодирующие слова, нам надо пройти по стрелкам от начальных символов к концу получившегося бинарного дерева. Так, для символа с вероятностью p4, получим B4=101, для p3 получим B3=100, для p2 получим B2=11, для p1 получим B1=0. Что означает схему:
a1 — 0, a2 — 11 a3 — 100 a4 — 101
Эта схема представляет собой префиксный код, являющийся кодом Хаффмана. Самый часто встречающийся в потоке символ a1 мы будем кодировать самым коротким словом 0, а самый редко встречающийся a4 длинным словом 101.
Для последовательности из 100 символов, в которой символ a1 встретится 50 раз, символ a2 — 24 раза, символ a3 — 15 раз, а символ a4 — 11 раз, данный код позволит получить последовательность из 176 бит ( 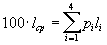 ). Т.е. в среднем мы потратим 1.76 бита на символ потока.
Доказательства теоремы, а также того, что построенная схема действительно задает код Хаффмана, смотри в [10].
Как стало понятно из изложенного выше, классический алгоритм Хаффмана требует записи в файл таблицы соответствия кодируемых символов и кодирующих цепочек.
На практике используются его разновидности. Так, в некоторых случаях резонно либо использовать постоянную таблицу, либо строить ее “адаптивно”, т.е. в процессе архивации/разархивации. Эти приемы избавляют нас от двух проходов по изображению и необходимости хранения таблицы вместе с файлом. Кодирование с фиксированной таблицей применяется в качестве последнего этапа архивации в JPEG и в рассмотренном ниже алгоритме CCITT Group 3.
Характеристики классического алгоритма Хаффмана:
Коэффициенты компрессии:8, 1,5, 1 (Лучший, средний, худший коэффициенты).
Класс изображений: Практически не применяется к изображениям в чистом виде. Обычно используется как один из этапов компрессии в более сложных схемах.
Симметричность: 2 (за счет того, что требует двух проходов по массиву сжимаемых данных).
Характерные особенности: Единственный алгоритм, который не увеличивает размера исходных данных в худшем случае (если не считать необходимости хранить таблицу перекодировки вместе с файлом). ). Т.е. в среднем мы потратим 1.76 бита на символ потока.
Доказательства теоремы, а также того, что построенная схема действительно задает код Хаффмана, смотри в [10].
Как стало понятно из изложенного выше, классический алгоритм Хаффмана требует записи в файл таблицы соответствия кодируемых символов и кодирующих цепочек.
На практике используются его разновидности. Так, в некоторых случаях резонно либо использовать постоянную таблицу, либо строить ее “адаптивно”, т.е. в процессе архивации/разархивации. Эти приемы избавляют нас от двух проходов по изображению и необходимости хранения таблицы вместе с файлом. Кодирование с фиксированной таблицей применяется в качестве последнего этапа архивации в JPEG и в рассмотренном ниже алгоритме CCITT Group 3.
Характеристики классического алгоритма Хаффмана:
Коэффициенты компрессии:8, 1,5, 1 (Лучший, средний, худший коэффициенты).
Класс изображений: Практически не применяется к изображениям в чистом виде. Обычно используется как один из этапов компрессии в более сложных схемах.
Симметричность: 2 (за счет того, что требует двух проходов по массиву сжимаемых данных).
Характерные особенности: Единственный алгоритм, который не увеличивает размера исходных данных в худшем случае (если не считать необходимости хранить таблицу перекодировки вместе с файлом).
|
JBIG
Алгоритм разработан группой экспертов ISO (Joint Bi-level Experts Group) специально для сжатия однобитных черно-белых изображений [5]. Например, факсов или отсканированных документов. В принципе, может применяться и к 2-х, и к 4-х битовым картинкам. При этом алгоритм разбивает их на отдельные битовые плоскости. JBIG позволяет управлять такими параметрами, как порядок разбиения изображения на битовые плоскости, ширина полос в изображении, уровни масштабирования. Последняя возможность позволяет легко ориентироваться в базе больших по размерам изображений, просматривая сначала их уменьшенные копии. Настраивая эти параметры, можно использовать описанный выше эффект “огрубленного изображения” при получении изображения по сети или по любому другому каналу, пропускная способность которого мала по сравнению с возможностями процессора. Распаковываться изображение на экране будет постепенно, как бы медленно “проявляясь”. При этом человек начинает анализировать картинку задолго до конца процесса разархивации.
Алгоритм построен на базе Q-кодировщика [6], патентом на который владеет IBM. Q-кодер, так же как и алгоритм Хаффмана, использует для чаще появляющихся символов короткие цепочки, а для реже появляющихся — длинные. Однако, в отличие от него, в алгоритме используются и последовательности символов.
Алгоритмы архивации с потерями
Алгоритм JPEG
JPEG — один из самых новых и достаточно мощных алгоритмов. Практически он является стандартом де-факто для полноцветных изображений [1]. Оперирует алгоритм областями 8х8, на которых яркость и цвет меняются сравнительно плавно. Вследствие этого, при разложении матрицы такой области в двойной ряд по косинусам (см. формулы ниже) значимыми оказываются только первые коэффициенты. Таким образом, сжатие в JPEG осуществляется за счет плавности изменения цветов в изображении.
Алгоритм разработан группой экспертов в области фотографии специально для сжатия 24-битных изображений. JPEG — Joint Photographic Expert Group — подразделение в рамках ISO — Международной организации по стандартизации. Название алгоритма читается ['jei'peg]. В целом алгоритм основан на дискретном косинусоидальном преобразовании (в дальнейшем ДКП), применяемом к матрице изображения для получения некоторой новой матрицы коэффициентов. Для получения исходного изображения применяется обратное преобразование.
ДКП раскладывает изображение по амплитудам некоторых частот. Таким образом, при преобразовании мы получаем матрицу, в которой многие коэффициенты либо близки, либо равны нулю. Кроме того, благодаря несовершенству человеческого зрения, можно аппроксимировать коэффициенты более грубо без заметной потери качества изображения.
Для этого используется квантование коэффициентов (quantization). В самом простом случае — это арифметический побитовый сдвиг вправо. При этом преобразовании теряется часть информации, но могут достигаться большие коэффициенты сжатия.
Как работает алгоритм
Итак, рассмотрим алгоритм подробнее. Пусть мы сжимаем 24-битное изображение.
Шаг 1.
Переводим изображение из цветового пространства RGB, с компонентами, отвечающими за красную (Red), зеленую (Green) и синюю (Blue) составляющие цвета точки, в цветовое пространство YCrCb (иногда называют YUV).
В нем Y — яркостная составляющая, а Cr, Cb — компоненты, отвечающие за цвет (хроматический красный и хроматический синий). За счет того, что человеческий глаз менее чувствителен к цвету, чем к яркости, появляется возможность архивировать массивы для Cr и Cb компонент с большими потерями и, соответственно, большими коэффициентами сжатия. Подобное преобразование уже давно используется в телевидении. На сигналы, отвечающие за цвет, там выделяется более узкая полоса частот.
Упрощенно перевод из цветового пространства RGB в цветовое пространство YCrCb можно представить с помощью матрицы перехода:
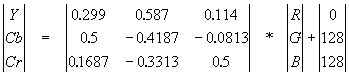 Обратное преобразование осуществляется умножением вектора YUV на обратную матрицу.
Обратное преобразование осуществляется умножением вектора YUV на обратную матрицу.
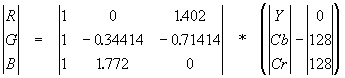 Шаг 2.
Разбиваем исходное изображение на матрицы 8х8. Формируем из каждой три рабочие матрицы ДКП — по 8 бит отдельно для каждой компоненты. При больших коэффициентах сжатия этот шаг может выполняться чуть сложнее. Изображение делится по компоненте Y — как и в первом случае, а для компонент Cr и Cb матрицы набираются через строчку и через столбец. Т.е. из исходной матрицы размером 16x16 получается только одна рабочая матрица ДКП. При этом, как нетрудно заметить, мы теряем 3/4 полезной информации о цветовых составляющих изображения и получаем сразу сжатие в два раза. Мы можем поступать так благодаря работе в пространстве YCrCb. На результирующем RGB изображении, как показала практика, это сказывается несильно.
Шаг 3.
Применяем ДКП к каждой рабочей матрице. При этом мы получаем матрицу, в которой коэффициенты в левом верхнем углу соответствуют низкочастотной составляющей изображения, а в правом нижнем — высокочастотной.
В упрощенном виде это преобразование можно представить так:
Шаг 2.
Разбиваем исходное изображение на матрицы 8х8. Формируем из каждой три рабочие матрицы ДКП — по 8 бит отдельно для каждой компоненты. При больших коэффициентах сжатия этот шаг может выполняться чуть сложнее. Изображение делится по компоненте Y — как и в первом случае, а для компонент Cr и Cb матрицы набираются через строчку и через столбец. Т.е. из исходной матрицы размером 16x16 получается только одна рабочая матрица ДКП. При этом, как нетрудно заметить, мы теряем 3/4 полезной информации о цветовых составляющих изображения и получаем сразу сжатие в два раза. Мы можем поступать так благодаря работе в пространстве YCrCb. На результирующем RGB изображении, как показала практика, это сказывается несильно.
Шаг 3.
Применяем ДКП к каждой рабочей матрице. При этом мы получаем матрицу, в которой коэффициенты в левом верхнем углу соответствуют низкочастотной составляющей изображения, а в правом нижнем — высокочастотной.
В упрощенном виде это преобразование можно представить так:
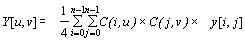 где
где 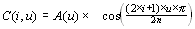
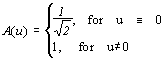 Шаг 4.
Производим квантование. В принципе, это просто деление рабочей матрицы на матрицу квантования поэлементно. Для каждой компоненты (Y, U и V), в общем случае, задается своя матрица квантования q[u,v] (далее МК).
Шаг 4.
Производим квантование. В принципе, это просто деление рабочей матрицы на матрицу квантования поэлементно. Для каждой компоненты (Y, U и V), в общем случае, задается своя матрица квантования q[u,v] (далее МК).
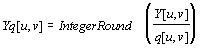 На этом шаге осуществляется управление степенью сжатия, и происходят самые большие потери. Понятно, что, задавая МК с большими коэффициентами, мы получим больше нулей и, следовательно, большую степень сжатия.
В стандарт JPEG включены рекомендованные МК, построенные опытным путем. Матрицы для большего или меньшего коэффициентов сжатия получают путем умножения исходной матрицы на некоторое число gamma.
С квантованием связаны и специфические эффекты алгоритма. При больших значениях коэффициента gamma потери в низких частотах могут быть настолько велики, что изображение распадется на квадраты 8х8. Потери в высоких частотах могут проявиться в так называемом “эффекте Гиббса”, когда вокруг контуров с резким переходом цвета образуется своеобразный “нимб”.
Шаг 5.
Переводим матрицу 8x8 в 64-элементный вектор при помощи “зигзаг”-сканирования, т.е. берем элементы с индексами (0,0), (0,1), (1,0), (2,0)...
На этом шаге осуществляется управление степенью сжатия, и происходят самые большие потери. Понятно, что, задавая МК с большими коэффициентами, мы получим больше нулей и, следовательно, большую степень сжатия.
В стандарт JPEG включены рекомендованные МК, построенные опытным путем. Матрицы для большего или меньшего коэффициентов сжатия получают путем умножения исходной матрицы на некоторое число gamma.
С квантованием связаны и специфические эффекты алгоритма. При больших значениях коэффициента gamma потери в низких частотах могут быть настолько велики, что изображение распадется на квадраты 8х8. Потери в высоких частотах могут проявиться в так называемом “эффекте Гиббса”, когда вокруг контуров с резким переходом цвета образуется своеобразный “нимб”.
Шаг 5.
Переводим матрицу 8x8 в 64-элементный вектор при помощи “зигзаг”-сканирования, т.е. берем элементы с индексами (0,0), (0,1), (1,0), (2,0)...
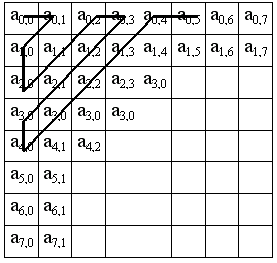 Таким образом, в начале вектора мы получаем коэффициенты матрицы, соответствующие низким частотам, а в конце — высоким.
Шаг 6.
Свертываем вектор с помощью алгоритма группового кодирования. При этом получаем пары типа (пропустить, число), где “пропустить” является счетчиком пропускаемых нулей, а “число” — значение, которое необходимо поставить в следующую ячейку. Так, вектор 42 3 0 0 0 -2 0 0 0 0 1 ... будет свернут в пары (0,42) (0,3) (3,-2) (4,1) ... .
Шаг 7.
Свертываем получившиеся пары кодированием по Хаффману с фиксированной таблицей.
Процесс восстановления изображения в этом алгоритме полностью симметричен. Метод позволяет сжимать некоторые изображения в 10-15 раз без серьезных потерь.
Таким образом, в начале вектора мы получаем коэффициенты матрицы, соответствующие низким частотам, а в конце — высоким.
Шаг 6.
Свертываем вектор с помощью алгоритма группового кодирования. При этом получаем пары типа (пропустить, число), где “пропустить” является счетчиком пропускаемых нулей, а “число” — значение, которое необходимо поставить в следующую ячейку. Так, вектор 42 3 0 0 0 -2 0 0 0 0 1 ... будет свернут в пары (0,42) (0,3) (3,-2) (4,1) ... .
Шаг 7.
Свертываем получившиеся пары кодированием по Хаффману с фиксированной таблицей.
Процесс восстановления изображения в этом алгоритме полностью симметричен. Метод позволяет сжимать некоторые изображения в 10-15 раз без серьезных потерь.
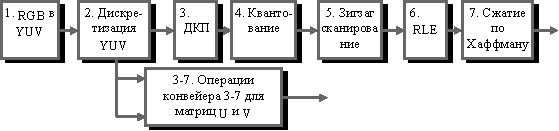 Конвейер операций, используемый в алгоритме JPEG.
Существенными положительными сторонами алгоритма является то, что: Конвейер операций, используемый в алгоритме JPEG.
Существенными положительными сторонами алгоритма является то, что:
|
Фрактальный алгоритм
Идея метода
Фрактальная архивация основана на том, что мы представляем изображение в более компактной форме — с помощью коэффициентов системы итерируемых функций (Iterated Function System — далее по тексту как IFS). Прежде, чем рассматривать сам процесс архивации, разберем, как IFS строит изображение, т.е. процесс декомпрессии.
Строго говоря, IFS представляет собой набор трехмерных аффинных преобразований, в нашем случае переводящих одно изображение в другое. Преобразованию подвергаются точки в трехмерном пространстве (х_координата, у_координата, яркость).
Наиболее наглядно этот процесс продемонстрировал Барнсли в своей книге “Fractal Image Compression”. Там введено понятие Фотокопировальной Машины, состоящей из экрана, на котором изображена исходная картинка, и системы линз, проецирующих изображение на другой экран:
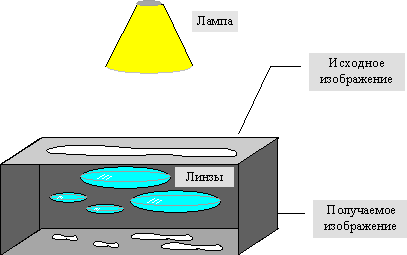 Расставляя линзы и меняя их характеристики, мы можем управлять получаемым изображением. Одна итерация работы Машины заключается в том, что по исходному изображению с помощью проектирования строится новое, после чего новое берется в качестве исходного. Утверждается, что в процессе итераций мы получим изображение, которое перестанет изменяться. Оно будет зависеть только от расположения и характеристик линз, и не будет зависеть от исходной картинки. Это изображение называется “неподвижной точкой” или аттрактором данной IFS. Соответствующая теория гарантирует наличие ровно одной неподвижной точки для каждой IFS.
Поскольку отображение линз является сжимающим, каждая линза в явном виде задает самоподобные области в нашем изображении. Благодаря самоподобию мы получаем сложную структуру изображения при любом увеличении. Таким образом, интуитивно понятно, что система итерируемых функций задает фрактал (нестрого — самоподобный математический объект).
Наиболее известны два изображения, полученных с помощью IFS: “треугольник Серпинского” и “папоротник Барнсли”. “Треугольник Серпинского” задается тремя, а “папоротник Барнсли” четырьмя аффинными преобразованиями (или, в нашей терминологии, “линзами”). Каждое преобразование кодируется буквально считанными байтами, в то время как изображение, построенное с их помощью, может занимать и несколько мегабайт.
Расставляя линзы и меняя их характеристики, мы можем управлять получаемым изображением. Одна итерация работы Машины заключается в том, что по исходному изображению с помощью проектирования строится новое, после чего новое берется в качестве исходного. Утверждается, что в процессе итераций мы получим изображение, которое перестанет изменяться. Оно будет зависеть только от расположения и характеристик линз, и не будет зависеть от исходной картинки. Это изображение называется “неподвижной точкой” или аттрактором данной IFS. Соответствующая теория гарантирует наличие ровно одной неподвижной точки для каждой IFS.
Поскольку отображение линз является сжимающим, каждая линза в явном виде задает самоподобные области в нашем изображении. Благодаря самоподобию мы получаем сложную структуру изображения при любом увеличении. Таким образом, интуитивно понятно, что система итерируемых функций задает фрактал (нестрого — самоподобный математический объект).
Наиболее известны два изображения, полученных с помощью IFS: “треугольник Серпинского” и “папоротник Барнсли”. “Треугольник Серпинского” задается тремя, а “папоротник Барнсли” четырьмя аффинными преобразованиями (или, в нашей терминологии, “линзами”). Каждое преобразование кодируется буквально считанными байтами, в то время как изображение, построенное с их помощью, может занимать и несколько мегабайт.
|
 =>
=> 
В худшем случае, если не будет применяться оптимизирующий алгоритм, потребуется перебор и сравнение всех возможных фрагментов изображения разного размера. Даже для небольших изображений при учете дискретности мы получим астрономическое число перебираемых вариантов. Причем, даже резкое сужение классов преобразований, например, за счет масштабирования только в определенное количество раз, не дает заметного выигрыша во времени. Кроме того, при этом теряется качество изображения. Подавляющее большинство исследований в области фрактальной компрессии сейчас направлены на уменьшение времени архивации, необходимого для получения качественного изображения.
Далее приводятся основные определения и теоремы, на которых базируется фрактальная компрессия. Этот материал более детально и с доказательствами рассматривается в [3] и в [4].
Определение. Преобразование 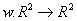 , представимое в виде , представимое в виде
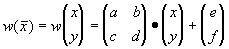 где a, b, c, d, e, f действительные числа и
где a, b, c, d, e, f действительные числа и 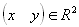 называется двумерным аффинным преобразованием.
Определение. Преобразование называется двумерным аффинным преобразованием.
Определение. Преобразование 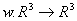 , представимое в виде , представимое в виде
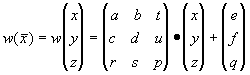 где a, b, c, d, e, f, p, q, r, s, t, u действительные числа и
где a, b, c, d, e, f, p, q, r, s, t, u действительные числа и 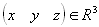 называется трехмерным аффинным преобразованием.
Определение. Пусть называется трехмерным аффинным преобразованием.
Определение. Пусть 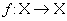 — преобразование в пространстве Х. Точка — преобразование в пространстве Х. Точка 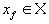 такая, что такая, что 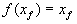 называется неподвижной точкой (аттрактором) преобразования.
Определение. Преобразование называется неподвижной точкой (аттрактором) преобразования.
Определение. Преобразование 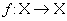 в метрическом пространстве (Х, d) называется сжимающим, если существует число s: в метрическом пространстве (Х, d) называется сжимающим, если существует число s: 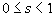 , такое, что , такое, что
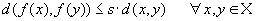 Замечание: Формально мы можем использовать любое сжимающее отображение при фрактальной компрессии, но реально используются лишь трехмерные аффинные преобразования с достаточно сильными ограничениями на коэффициенты.
Теорема. (О сжимающем преобразовании)
Пусть
Замечание: Формально мы можем использовать любое сжимающее отображение при фрактальной компрессии, но реально используются лишь трехмерные аффинные преобразования с достаточно сильными ограничениями на коэффициенты.
Теорема. (О сжимающем преобразовании)
Пусть 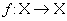 в полном метрическом пространстве (Х, d). Тогда существует в точности одна неподвижная точка в полном метрическом пространстве (Х, d). Тогда существует в точности одна неподвижная точка 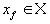 этого преобразования, и для любой точки этого преобразования, и для любой точки 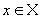 последовательность последовательность 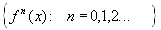 сходится к сходится к 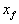 .
Более общая формулировка этой теоремы гарантирует нам сходимость.
Определение. Изображением называется функция S, определенная на единичном квадрате и принимающая значения от 0 до 1 или .
Более общая формулировка этой теоремы гарантирует нам сходимость.
Определение. Изображением называется функция S, определенная на единичном квадрате и принимающая значения от 0 до 1 или 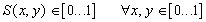 Пусть трехмерное аффинное преобразование
Пусть трехмерное аффинное преобразование 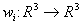 , записано в виде , записано в виде
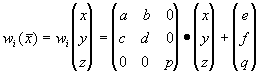 и определено на компактном подмножестве
и определено на компактном подмножестве 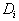 декартова квадрата [0..1]x[0..1]. Тогда оно переведет часть поверхности S в область декартова квадрата [0..1]x[0..1]. Тогда оно переведет часть поверхности S в область 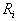 , расположенную со сдвигом (e,f) и поворотом, заданным матрицей , расположенную со сдвигом (e,f) и поворотом, заданным матрицей
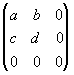 .
При этом, если интерпретировать значение S как яркость соответствующих точек, она уменьшится в p раз (преобразование обязано быть сжимающим) и изменится на сдвиг q.
Определение. Конечная совокупность W сжимающих трехмерных аффинных преобразований .
При этом, если интерпретировать значение S как яркость соответствующих точек, она уменьшится в p раз (преобразование обязано быть сжимающим) и изменится на сдвиг q.
Определение. Конечная совокупность W сжимающих трехмерных аффинных преобразований 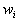 , определенных на областях , определенных на областях 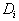 , таких, что , таких, что 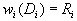 и и 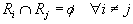 , называется системой итерируемых функций (IFS).
Системе итерируемых функций однозначно сопоставляется неподвижная точка — изображение. Таким образом, процесс компрессии заключается в поиске коэффициентов системы, а процесс декомпрессии — в проведении итераций системы до стабилизации полученного изображения (неподвижной точки IFS). На практике бывает достаточно 7-16 итераций. Области , называется системой итерируемых функций (IFS).
Системе итерируемых функций однозначно сопоставляется неподвижная точка — изображение. Таким образом, процесс компрессии заключается в поиске коэффициентов системы, а процесс декомпрессии — в проведении итераций системы до стабилизации полученного изображения (неподвижной точки IFS). На практике бывает достаточно 7-16 итераций. Области 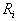 в дальнейшем будут именоваться ранговыми, а области в дальнейшем будут именоваться ранговыми, а области 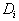 — доменными.
Построение алгоритма
Как уже стало очевидным из изложенного выше, основной задачей при компрессии фрактальным алгоритмом является нахождение соответствующих аффинных преобразований. В самом общем случае мы можем переводить любые по размеру и форме области изображения, однако в этом случае получается астрономическое число перебираемых вариантов разных фрагментов, которое невозможно обработать на текущий момент даже на суперкомпьютере.
В учебном варианте алгоритма, изложенном далее, сделаны следующие ограничения на области: — доменными.
Построение алгоритма
Как уже стало очевидным из изложенного выше, основной задачей при компрессии фрактальным алгоритмом является нахождение соответствующих аффинных преобразований. В самом общем случае мы можем переводить любые по размеру и форме области изображения, однако в этом случае получается астрономическое число перебираемых вариантов разных фрагментов, которое невозможно обработать на текущий момент даже на суперкомпьютере.
В учебном варианте алгоритма, изложенном далее, сделаны следующие ограничения на области:
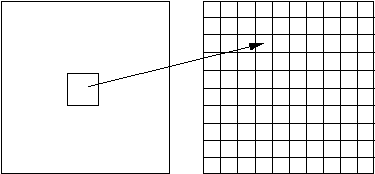 Эти ограничения позволяют:
Эти ограничения позволяют:
|
Рекурсивный (волновой) алгоритм
Английское название рекурсивного сжатия — wavelet. На русский язык оно переводится как волновое сжатие, и как сжатие с использованием всплесков. Этот вид архивации известен довольно давно и напрямую исходит из идеи использования когерентности областей. Ориентирован алгоритм на цветные и черно-белые изображения с плавными переходами. Идеален для картинок типа рентгеновских снимков. Коэффициент сжатия задается и варьируется в пределах 5-100. При попытке задать больший коэффициент на резких границах, особенно проходящих по диагонали, проявляется “лестничный эффект” — ступеньки разной яркости размером в несколько пикселов.
Идея алгоритма заключается в том, что мы сохраняем в файл разницу — число между средними значениями соседних блоков в изображении, которая обычно принимает значения, близкие к 0.
Так два числа a2i и a2i+1 всегда можно представить в виде b1i=(a2i+a2i+1)/2 и b2i=(a2i-a2i+1)/2. Аналогично последовательность ai может быть попарно переведена в последовательность b1,2i.
Разберем конкретный пример: пусть мы сжимаем строку из 8 значений яркости пикселов (ai): (220, 211, 212, 218, 217, 214, 210, 202). Мы получим следующие последовательности b1i, и b2i: (215.5, 215, 215.5, 206) и (4.5, -3, 1.5, 4). Заметим, что значения b2i достаточно близки к 0. Повторим операцию, рассматривая b1i как ai. Данное действие выполняется как бы рекурсивно, откуда и название алгоритма. Мы получим из (215.5, 215, 215.5, 206): (215.25, 210.75) (0.25, 4.75). Полученные коэффициенты, округлив до целых и сжав, например, с помощью алгоритма Хаффмана с фиксированными таблицами, мы можем поместить в файл.
Заметим, что мы применяли наше преобразование к цепочке только два раза. Реально мы можем позволить себе применение wavelet- преобразования 4-6 раз. Более того, дополнительное сжатие можно получить, используя таблицы алгоритма Хаффмана с неравномерным шагом (т.е. нам придется сохранять код Хаффмана для ближайшего в таблице значения). Эти приемы позволяют достичь заметных коэффициентов сжатия.
Упражнение: Мы восстановили из файла цепочку (215, 211) (0, 5) (5, -3, 2, 4) (см. пример). Постройте строку из восьми значений яркости пикселов, которую воссоздаст алгоритм волнового сжатия.
Алгоритм для двумерных данных реализуется аналогично. Если у нас есть квадрат из 4 точек с яркостями a2i,2j, a2i+1, 2j, a2i, 2j+1, и a2i+1, 2j+1, то
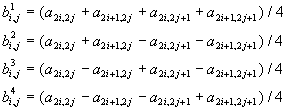
Используя эти формулы, мы для изображения 512х512 пикселов получим после первого преобразования 4 матрицы размером 256х256 элементов: |
 --
-- 
В первой, как легко догадаться, будет храниться уменьшенная копия изображения. Во второй — усредненные разности пар значений пикселов по горизонтали. В третьей — усредненные разности пар значений пикселов по вертикали. В четвертой — усредненные разности значений пикселов по диагонали. По аналогии с двумерным случаем мы можем повторить наше преобразование и получить вместо первой матрицы 4 матрицы размером 128х128. Повторив наше преобразование в третий раз, мы получим в итоге: 4 матрицы 64х64, 3 матрицы 128х128 и 3 матрицы 256х256. На практике при записи в файл, значениями, получаемыми в последней строке ( 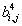 ), обычно пренебрегают (сразу получая выигрыш примерно на треть размера файла — 1- 1/4 - 1/16 - 1/64...).
К достоинствам этого алгоритма можно отнести то, что он очень легко позволяет реализовать возможность постепенного “прояв–ления” изображения при передаче изображения по сети. Кроме того, поскольку в начале изображения мы фактически храним его уменьшенную копию, упрощается показ “огрубленного” изображения по заголовку.
В отличие от JPEG и фрактального алгоритма данный метод не оперирует блоками, например, 8х8 пикселов. Точнее, мы оперируем блоками 2х2, 4х4, 8х8 и т.д. Однако за счет того, что коэффициенты для этих блоков мы сохраняем независимо, мы можем достаточно легко избежать дробления изображения на “мозаичные” квадраты.
Характеристики волнового алгоритма:
Коэффициенты компрессии: 2-200 (Задается пользователем).
Класс изображений:Как у фрактального и JPEG.
Симметричность: ~1.5
Характерные особенности: Кроме того, при высокой степени сжатия изображение распадается на отдельные блоки. ), обычно пренебрегают (сразу получая выигрыш примерно на треть размера файла — 1- 1/4 - 1/16 - 1/64...).
К достоинствам этого алгоритма можно отнести то, что он очень легко позволяет реализовать возможность постепенного “прояв–ления” изображения при передаче изображения по сети. Кроме того, поскольку в начале изображения мы фактически храним его уменьшенную копию, упрощается показ “огрубленного” изображения по заголовку.
В отличие от JPEG и фрактального алгоритма данный метод не оперирует блоками, например, 8х8 пикселов. Точнее, мы оперируем блоками 2х2, 4х4, 8х8 и т.д. Однако за счет того, что коэффициенты для этих блоков мы сохраняем независимо, мы можем достаточно легко избежать дробления изображения на “мозаичные” квадраты.
Характеристики волнового алгоритма:
Коэффициенты компрессии: 2-200 (Задается пользователем).
Класс изображений:Как у фрактального и JPEG.
Симметричность: ~1.5
Характерные особенности: Кроме того, при высокой степени сжатия изображение распадается на отдельные блоки.
|
Дата добавления: 2015-08-21; просмотров: 2283;
