Физические представления и гипотезы, формализация закона сохранения

Принципиальным отличием естественных наук от «не естественных» является отсутствие у последних переменных, в которых необходимо думать. Поэтому приведем несколько определений понятий, позволяющих в дальнейшем банковскому работнику понять физика.

1. Параметром состояния системы называется физическая величина, которая по мнению исследователя существенно определяет поведение системы. Заметим, что ключевыми словами здесь являются «физическая величина». Она характеризуется двумя составляющими: физическая величина это отвлеченное число + наименование, название ее. Например, длина ресниц секретарши президента банка может быть параметром состояния коммерческого банка: это действительно физическая величина и ее несложно измерить. Предостережем не физиков, что математические операции над отвлеченными числами не всегда можно проводить над физическими величинами. Например, операция алгебраического сложения имеет смысл над физическими величинами только одинаковой размерности. Складывать танки и ромашки нехорошо.

2. Потенциалом некоторого взаимодействия системы с внешней средой называется такой параметр состояния, разность значений которого в системе и во внешнем мире является необходимым условием обмена (энергией, массой, количеством движения, информацией и .... деньгами) системы с внешней средой.

3. Координатой состояния этого рода взаимодействия называется такой параметр состояния, изменение которого в системе (и, конечно, во внешнем мире) является достаточным условием обмена.

4. Уравнением состояния системы называется зависимость потенциала от всех координат.

5. Элементарным количеством воздействия внешнего мира данного рода на рассматриваемый объект называется произведение потенциала на приращение (дифференциал) координаты того же рода взаимодействия.

6. Первый закон термодинамики это запись закона сохранения некоторой субстанции: дифференциал ее равен сумме элементарных количеств воздействия всех родов внешней среды на рассматриваемую систему.

Итак, каждый род взаимодействия характеризуется своим потенциалом и координатой, а если последняя меняется, то и количеством взаимодействия. Далее, из этих определений понятий следует: сколько родов взаимодействия, столько потенциалов истолько уравнений состояния, столько слагаемых в первом законе термодинамики.

Чтобы понять, чем занимается коммерческий банк, каковы взаимодействия его с внешней средой, рассмотрим технологическую схему типичного коммерческого банка на рис. 9.1.

Банк территориально расположен в некотором регионе, население которого получает доходы от своей деятельности. Часть доходов уходит на потребление (ради этого и осуществляется эта деятельность), остаток образует накопление. Физические лица делают накопления для приобретения дорогостоящих товаров, предметов потребления и услуг. Юридические лица (корпоративные вкладчики), открыв свой счет в банке, делают накопления для обновления производства, приобретения нового оборудования, для расширения производства.

Эти накопления вкладчики приносят в банк, и их деньги являются сырьем для банка, для совершения некоторых переделов над этим сырьем. Все вклады собираются в емкость под названием «актив». Каждый вклад и все разнообразие вкладов характеризуется суммой вклада, сроком возврата и банковским % по вкладу.

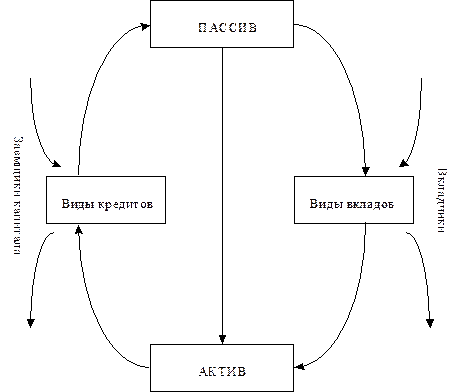
Рис. 9.1. Технологическая схема типичного коммерческого банка.

Далее сырье из емкости «актив» направляется в различные операции, процедуры, которые при всем их разнообразии в сути и в названиях носят чисто кредитный характер. В банк приходят заемщики капитала и получают некоторую сумму денег для своих надобностей. Каждый кредит характеризуется суммой, сроком возврата и платой за кредит в виде банковского % за кредит.

При наступлении срока возврата кредита заемщик капитала выполняет свои обязательства перед банком, т.е. возвращает долг с %-ми, который идет в емкость под названием «пассив». Из этой емкости банк выполняет свои обязательства перед вкладчиками, а доходы от кредита направляет в «актив».

Таким образом, технологическая схема коммерческого банка замкнута, имеет контур в контуре. По большому контуру движутся деньги вкладчиков, по малому, внутреннему контуру и деньги вкладчиков и доходы банка от кредитных операций.

Из опыта разработки, пуска и эксплуатации химико-технологических систем известно, что такая схема крайне неустойчива и нестабильна. Владельцы банковского капитала это хорошо знают по собственному печальному опыту и пытаются принимать «успокоительные» меры.

Но не будем отвлекаться на надежность коммерческого банка, это особая тема, отправимся в намеченный путь построения термодинамики коммерческого банка. Из технологической схемы банка видно, что он испытывает существенные воздействия внешней среды по крайней мере трех родов.

1. Воздействие вкладчиков. Что, собственно, заставляет, стимулирует вкладчика отдавать, хоть и на время, свои деньги - накопления в банк? Суть главной гипотезы нашего рассмотрения состоит в том, что вкладчики хотят, простите, «халявы»: «Меньше дать, больше взять, да еще побыстрее.». Формализуем это очаровательное желание.

Пусть N(t = 0) - величина вклада в начальный момент времени. Прирост меновой стоимости этого вклада характеризуется уравнением:

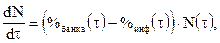при

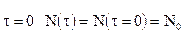
где %_БАНКА(t) - банковский процент по вкладу, выраженный не в %, а в долях. Размерность его (день)^-1. %_ИНФ(t) - процент инфляции, (день)^-1. Заметим, что невежественный вкладчик не подозревает об инфляции, т.е. уменьшения меновой стоимости его денег за время вклада. К моменту времени t + Dt, где Dt - срок депозита

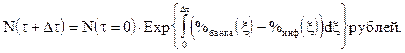
Заметим, что %_БАНКА(t) здесь записан функцией от времени. Наш дорогой сбербанк позволяет себе без согласия и уведомления вкладчиков менять %_БАНКА , как в любой бандитской стране. То обстоятельство, что %_ИНФ(t) является функцией от времени чувствует, хотя и не понимает, любая старушка в магазине: «Опять цены выросли!»

Величина прибыли вкладчика в меновой стоимости равна:

N(τ + Δτ) – N(τ = 0) = Exp{∫(%_банка(ξ) - %_инф(ξ))dξ, рублей.

А норма прибыли соответственно равна:

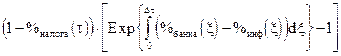рублей прибыли / рубль затрат.

Чтобы отразить стремление биологического вида homo sapience не просто к «халяве», а к быстрой «халяве», разделим норму прибыли на время депозита Dt. Тогда потенциалом P_N воздействия вкладчиков на банк (или банка на вкладчиков) назовем именно эту скорость нормы прибыли:

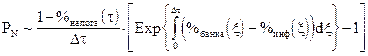(9.1)

рублей прибыли / рубль затрат* день.

Обращаем внимание читателя с гуманитарным образованием, что 1 рубль в кармане покупателя ¹ 1 рублю в банке, ¹ 1 рублю налога, ¹ 1 рублю прибыли; что 1% налога ¹ 1% инфляции ¹ 1 % банка ¹ 1% кредита и т.д. Вроде бы, там рубли, там %-ты, но это разныерубли и %-ты, т.е. разные физические величины, так как они имеют разное наименование.

Всякий банк имеет собственный капитал, который он пускает по внутреннему контуру (см. рис. 9.1), чтобы получить доход от кредитных операций. А так как банковские владельцы капитала принадлежат к тому же биологическому типу, что и вкладчики, то выражение P_N будет тем же, только их %_БАНКА(t) º 0, но для нашей модели это не существенно.

В качестве координаты состояния, обусловленного этим видом воздействия, примем одномоментное количество накоплений N, находящихся в распоряжении банка. В величине N находятся средства частных и юридических лиц, кредит от «дружественных» банков и собственные высоко ликвидные средства. Размерность N - рубли.

2. Воздействие заемщиков капитала. Повторимся, что при всем разнообразии операций, процедур и услуг заемщикам капитала все они носят кредитный характер. Разобьем всю сумму активов банка на две части:

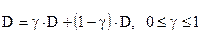
где g - доля активов, направленных на операции с ценными бумагами, и 1 - g - доля, направленная на кредитование промышленности, торговли и производства услуг. Величину g определяет руководство коммерческим банком или акционерное собрание.

Рассмотрим операции с ценными бумагами (векселями, валютой, государственными казначейскими облигациями, акциями каких-то фирм и т. д.). Пусть X₀ - стоимость ценной бумаги у эмитента (продавца), который гарантирует некоторый доход в виде % от X₀ через какой-то промежуток времени Dt дней. Пусть X - рыночная стоимость этой ценной бумаги на рынке. Биржевой курс ценной бумаги, выраженный не в %, а в долях от 1, представляется в виде:

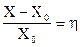
Если h > 0, да еще и увеличивается от торга к торгу, то предприятие - эмитент неплохо работает, если h уменьшается и становится отрицательным, то такое предприятие явно разоряется.

Если банк покупает ценные бумаги с общей стоимостью X₀ эмитента, то на рынке он затратит

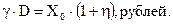
После реализации ценных бумаг, после их погашения эмитент обязан выдать владельцу сумму X₀ плюс доход %*X₀ рублей. Следовательно, доход банка от операции с ценными бумагами составит величину:

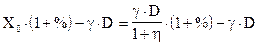
Из этого выражения следует, что не отрицательность дохода будет при % ³ h, т.е. биржевой курс ценной бумаги должен не превосходить доходности ее, иначе банк потерпит убыток.

Прибыль получается после уплаты налогов государству, т.е.

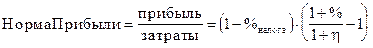рублей прибыли / рубль затрат,

Скорость нормы прибыли получим делением нормы прибыли на время операции с ценными бумагами Dt:

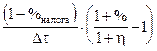рублей прибыли / рубль затрат в день.

Рассмотрим процесс кредитования банком промышленности, торговли и производства услуг. Если банк дает кредит в размере (1 - g)D рублей, то хочет получить через Dt_КРЕДИТ дней обратно всю эту сумму плюс плату за кредит в размере %_КРЕДИТ*(1 - g)D рублей. Доход банка составит:

Прибыль будет равна:

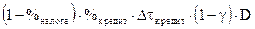рублей прибыли.

Норма прибыли представится выражением:

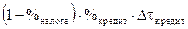рублей прибыли / рубль затрат.

Скорость нормы прибыли имеет совсем простое выражение:

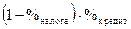рублей прибыли / рубль затрат в день.

Общая скорость нормы прибыли от всех кредитных операций коммерческого банка равна сумме скоростей, но с весом g и 1 - g. Отсюда потенциал P_D взаимодействия банка и заемщиков капитала пропорционален

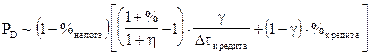(9.2)

Координатой состояния второго рода взаимодействия банка с внешним миром принимаем всю сумму кредитов D, одномоментно находящихся на руках заемщиков капитала. Говоря «банковским» языком, D представляет собой работающие (рисковые) активы.

3. Третий род взаимодействия. Само существование банковского механизма в некоторой среде невозможно без затрат на свое бытие. Банк должен платить за аренду помещения или земли, платить городу за коммунальные услуги, за все виды связи и энергию, за банковское оборудование и его обслуживание, приходится платить за охрану и заработную плату банковским наемным служащим и т.д. и т.п. Все эти затраты Z(t) по существу определяют себестоимость 1 рубля прибыли, ради которой и организован сам банк.

Часть этих затрат банку удается взвалить на плечи своих клиентов: банк требует оплаты за процедуру любого движения денег вкладчиков, владельцев счетов и заемщиков капитала, Обозначим этот новый груз на клиентов как ZZ(t) рублей поборов / год.

Потенциалом третьего рода взаимодействия внешней среды с банком назовем величину:

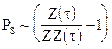(9.3)

Рассмотрим координату состояния этого рода взаимодействия. Чем больше видов операций, процедур и услуг может производить банк, тем, вообще-то, он больше привлекает к себе клиентов, но, одновременно, и больше поле проявления хаоса, беспорядка, ошибок персонала, сбоев и отказов банковского механизма. Если банк делает i = 1,2,3,...i₀ операций, процедур и услуг, и если каждая из них востребована m_i раз в год, а общее их число M, то m_i / M ® P_i есть частота свершения i-ой операции. Вводим меру разнообразия операций в банке по Шеннону:

i = 1,2,3,....i₀ .

Аналогично, как в теории надежности технологических систем, все виды ошибок, сбоев и отказов банковского механизма, безграмотные решения руководства, администраторов всех рангов разобьем на отдельные, узкие, специфичные группы. Пронумеруем эти группы j = 1,2,3,...j₀ . Из статистического анализа состояния банка за какой-то период времени можно получить вероятность отказов по каждой группе P₁,P₂,P₃,....P_j0 . Вводим меру хаоса и беспорядка в банке тоже в манере Шеннона

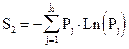j = 1,2,3,...j₀ .

Может быть, банковским деятелям будет интересно узнать, что максимум S₁ и S₂ наступает при P₁ = P₂ = P₃ =.... и эти максимумы равны max S₁ = ln i₀ и max S₂ = ln j₀ .

Третьей координатой состояния примем величину S = S₁ + S₂ .

Приведем уравнения состояния (9.1 – 9.3) P_N , P_D , P_S = f(N, D, S) от общего вида к наивозможно явной связи с операционными банковскими характеристиками, т.е. аргументами задачи N, D, S.

Сразу отметим экспериментальный факт в деятельности банков: время кредитных операций Dt_КРЕДИТ, как правило, меньше времени депозита Dt, времени вклада денег населением в банк. Последний старается много раз пропустить эти деньги по внутреннему технологическому контуру, получая доход при каждом таком обороте. Обозначим буквой c число таких оборотов. Тогда

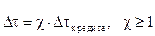
Относительно потенциала P_D = f(N, D, S) предположим, что он зависит от величины N, от доли актива a, которую банки держат в качестве резерва, и от меры хаоса и разнообразия. Эту зависимость представим в виде:

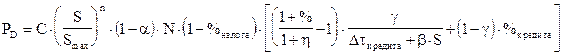(9.2`)

Здесь длительность банковской кредитной операции Dt_{КРЕДИТА} увеличили линейно на функцию от S, считая, что хаос и ошибки увеличивают протяженность во времени этой операции (b ³ 0). Размерность [b] = дни. Величина С - эмпирическая постоянная с размерностью (рубль)^-1. Сами величины С, n, a, b находятся экспериментально в процессе адаптации предлагаемой модели к какому-то конкретному банку.

Относительно потенциала вкладчика P_N можно предположить, что он не зависит от количества денег в активной кредитной форме D, но зависит от меры хаоса и разнообразия S:

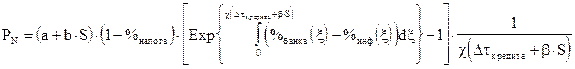(9.1`)

Наконец, выражение потенциала «бытия» банка во взаимосвязи с внешним миром представим в виде:

. (9.3`)

В (9.3`) предполагается, что этот потенциал пропорционален объему средств, находящихся в переработке банком, и обратно пропорционален времени кредита. Здесь коэффициент пропорциональности q и показатель степени m являются эмпирическими постоянными, свойственными каждому банку. Размерность величин q и m - нулевая.

И последнее соображение перед формальной записью первого закона термодинамики коммерческого банка. Рассматривая какой-то объект, термодинамический метод анализа требует обозначить некоторую абстрактную область и ее границу: внутри области находится изучаемый объект, снаружи - внешний мир. В каждой точке границы построим единичную нормаль, а о направлении ее (во внутрь или наружу) будем договариваться, т.к. это не принципиально. Всем людям нравится получать, и они расстраиваются, если надо платить и отдавать долги. В соответствии с этими эмоциями направим вектор единичной нормали во внутрь области, где находится банк. Тогда приход денег приносит радость, поэтому соответствующее элементарное количество внешнего воздействия пишем со знаком « +». В противном случае пишем знак минус.

Запишем сумму всех элементарных количеств воздействия внешнего мира на коммерческий банк с учетом замечания о знаках и приравняем ее дифференциалу некоторой функции U(N, D, S).

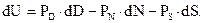(9.4)

Выражение (9.4) и представляет собой формальную запись «первого закона термодинамики» для коммерческого банка. Первое слагаемое (имеющее размерность «рубль прибыли / день», как и размерность остальных слагаемых) представляет собой скорость прихода прибыли от кредитных операций банка, второе - скорость прибыли вкладчиков, которую банк обязан обеспечить для них, третье - потери прибыли банка, связанные с «бытием» банка и расплата за хаос и беспорядок. Напомним, что в P_S входит зарплата служащих банка от уборщицы до президента, а в U входит прибыль, которую получат акционеры в виде дивидентов. Физический смысл функции U(N, D, S) - скорость прибыли банка.

Выражение (9.4) в сочетании с уравнениями состояния (9.1` - 9.3`) несет в себе максимум содержания в термодинамическом методе анализа. Больше ничего в нем нет, и в этом его сила, но в этом и его недостатки. Заметим, что нас не интересует микромир банка, нам не интересны взаимоотношения какого-то заведующего отделом с одним из вице президентов банка, мы не учитываем и не рассматриваем потоки денег, материи, информации внутри термодинамического объекта анализа. Мы рассматриваем коммерческий банк с большого расстояния и не видим деталей, которые крайне существенны для работников банка и его акционеров. Нас интересуют взаимодействия внешнего мира и организации, желающей извлекать прибыль из этого мира. И термодинамические закономерности этого взаимодействия полностью определяют жизнь банка, даже если его сотрудники об этом не подозревают.

2. Обработка модели и результаты.

1. Координата состояния S достигает максимума при соизмеримости S₁ и S₂. Следовательно, абсолютный максимум S происходит при i₀ = j₀ и равняется

.

Следовательно, если необходимо достичь роста или максимума S, необходимо делать меру разнообразия операций, процедур и услуг банка близкой к мере хаоса и беспорядка в банковском механизме. Естественное стремление банкиров уменьшить последнюю ведет к узкой специализации банков, что и наблюдается в истории развития банковской системы развитых стран.

Мера хаоса и беспорядка в банке зависит от условий труда его работников, их квалификации и опыта, совершенства банковского оборудования и вычислительных систем, уровнем некомпетентности и комплексами неполноценности руководителей всех рангов. Короче говоря, культура среды, в которую помещен банк, определяет надежность выполнения разнообразных технологических переделов.

Еще одно следствие: функция y = ln(x), x ³ 1 довольно сильно изменяется при небольших, близких к 1 значениях аргумента х, а далее с ростом х ее изменение не существенно. Это свойство логарифмической функции следует учитывать при любых реорганизациях банковского механизма, изменениях его структуры.

2. Рассмотрим вектор 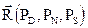и найдем скалярное произведение двух векторов 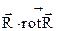. Равенство нулю этого произведения при ВСЕХ значениях аргументов N, D, S в области определения (9.1` - 9.3`) является необходимым условием полноты дифференциала dU в (9.4). Оказалось, что это произойдет при одновременном выполнении двух условий:

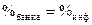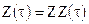и (9.5)

Первое условие означает, что вкладчики, получив в срок возврата большую сумму, чем ранее отдали, не увеличивают меновую стоимость своих денег, т.е. количество товаров и услуг могут приобрести по-прежнему столько же. Отечественный сбербанк практикует такое мероприятие постоянно, даже делает %_БАНКА < %_ИНФ., а вкладчикам деваться некуда, т.к. другие банки оказались ненадежными. В развитых странах реакция на (9.5) мгновенна: потенциал P_N = 0, и физические лица заберут свои вклады и будут искать другие способы капитализации своих накоплений.

Второе условие означает, что все затраты на содержание банка полностью лежат на клиентах банка, следовательно, клиентами могут быть только такие, для которых оплата услуг банка незначительна по сравнению с доходами от этих услуг. Следовательно, мелкие вкладчики должны быть отторгнуты банком.

Условия (9.5) могут быть реализованы при больших уставных, собственных капиталах банка, при широкой эмиссии их акций и высокой рыночной стоимости их на фондовых биржах. В этом случае банк запускает большие средства по внутреннему контуру (см. рис. 9.1) и становится ростовщиком, этаким Гопсеком.

Такая ситуация возникает лишь на малый промежуток времени и только для крупных банков, а для средних и мелких вообще исключена, так как без капиталов вкладчиков эти банки не могут существовать. Кроме того, конкуренция за вкладчиков между банками заставляет уменьшать поборы ZZ(t) и часто просто делать их нулевыми.

Итак, dU(N, D, S), как правило, не является полным дифференциалом, следовательно, функция U(N, D, S) является функцией процесса, а ее изменение DU(N, D, S) зависит от траектории движения банка в координатах (N, D, S).

Косвенным подтверждением этого математического следствия является сам способ прогнозирования стратегии развития, направления поведения банков в развитых странах. Суть этого способа состоит в следующем. Политическая, экономическая и социальная ситуация вокруг банка требует изменения (как правило, увеличения) функции U на величину DU. Команда экспертов или каждый из них предлагает набор мероприятий, обеспечивающий это задание. В нашей терминологии предлагается набор траекторий перехода с уровня U(N, D, S) на уровень U + DU. Каждый вариант мероприятий, предложенный экспертами, просчитывается на ЭВМ и далее отбирается оптимальный, наверное, по срокам реализации и по минимальным затратам. Просчет одного варианта, оказывается, очень дорогим делом (1 - 1,5 миллиона долларов), поэтому число просчитанных вариантов не может быть большим (для крупного банка < 10) и, в целом, такой способ «русского авось» очень дорог для поиска оптимальной стратегии развития банка. Но, кажется, Запад другого не знает, а специалисты в области точных, естественных наук не ведают о таких затруднениях своих дорогих и любимых банкиров, которые отчужденно варятся в своем соку вот уже не одну сотню лет.

3. Рассмотрим снова выражения (9.1` - 9.3`) уравнений состояния и выпишем все эмпирические параметры, свойственные какому-то конкретному банку: С, n, a, b, g, c, a, b, q, m - всего их 10. Во множестве всех коммерческих банков эти 10 параметров являются такими же независимыми переменными, аргументами задачи, как и координаты состояния N, D, S, Следовательно, каждый банк имеет 13 степеней свободы, Просто диву даешься, как господа банкиры могут управлять своим хозяйством. Научный сотрудник в области точных, естественных наук здесь сразу бы сдался.

Кроме указанных 13 степеней свободы в (9.1` - 9.3`) входят параметры внешнего мира: %_НАЛОГА на доходы банка и его клиентов, % доходности ценных бумаг, курсовая цена этих бумаг h, %_ИНФ, банковский %_БНК по вкладам. Следовательно, внешняя среда, куда помещен банк, характеризуется еще 5-ю параметрами.

Такое изобилие параметров задачи является следствием детальности рассмотрения процессов переноса в банковской технологии, хотя заведомо найдутся оппоненты, считающие эту детальность недостаточной. Множественность параметров в (9.4) не позволяет сделать обобщения и универсализацию результатов исследования.

Начнем решительно уменьшать размерность задачи без искажения ее сути. Рассмотрим частный случай: S = const. Он регулярно встречается в банковском деле в периоды между двумя соседними реконструкциями банка, между сменами приоритетов, целей и структуры банка. Для этого частного случая первый закон термодинамики коммерческого банка (автор уже храбро не ставит кавычек у этого набора слов) принимает двучленную форму:

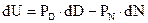, (9.4)

а координата состояния S становится параметром в сумме с 10 предыдущих.

Как принято в обобщенном анализе, обезразмерим (9.4) на соответствующие натуральные масштабы U_#, D_#, N_# и найдем систему определительных уравнений:

,

,

.

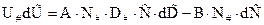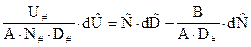Здесь величины с крышечками вверху - безразмерны. Система определительных уравнений имеет вид:

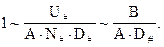
Выражения для А и В через параметры задачи легко прослеживаются в (9.1` - 9.2`). Итак, число искомых натуральных масштабов - 3, число независимых определительных уравнений -2, Причем видно, что масштаб D_# находится однозначно. Для поиска U_# и N_# придется привлечь информацию из внешней для банка среды, просто больше неоткуда, так как задача оказалась инвариантной к одному из двух оставшихся масштабов.

Масштаб N_# можно оценить следующим образом. Пусть в регионе, где территориально расположен коммерческий банк, имеется К рабочих мест в промышленности, сельском хозяйстве, в сфере услуг. Пусть средняя зарплата работников этого региона равна l, а минимальная потребительская корзина стоит р рублей в месяц. Тогда в течение года в банке будет накоплений не больше

.

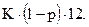Пусть в этом же регионе развили свою деятельность I фирм, юридических лиц, которые держат свои капиталы и оборотные средства J в рассматриваемом банке. Следовательно, оценка натурального масштаба N_# денежных средств, находящихся одномоментно в распоряжении коммерческого банка, имеет величину:

рублей.

Натуральный масштаб активно работающих средств банка D_# получаем из уравнения

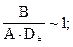
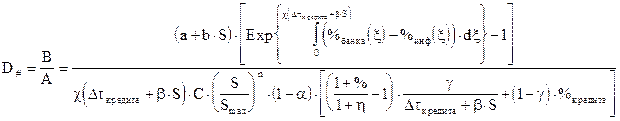
Натуральный масштаб искомой функции скорости прибыли U_# коммерческого банка получаем из уравнения:

или

В принципе это несложная алгебраическая процедура.

Физический смысл масштаба N_# ясен из предыдущего: это способность физических лиц к накоплению плюс оборотные и собственные средства фирм и предприятий, которые держат свои счета в банке. Вообще-то, все логично: в центре пустыни Сахара никто коммерческий банк не организует.

Натуральный масштаб D_# - размер активов банка, получен из условия соизмеримости скоростей нормы прибыли вкладчиков и самого банка от операций в кредитной сфере.

Натуральный масштаб U_# - скорость прибыли банка получен из условия, что скорость прибыли банка соизмерима со скоростью прибыли от кредитных операций.

Наверное, такой физический смысл полученных масштабов не вызовет особых возражений у специалистов банковского дела, работающих в условиях развитой рыночной экономики. В нашей стране, где пока «Боливар не вывезет двоих», эти рассуждения покажутся скучными.

В результате применения метода натуральных масштабов к первому закону термодинамики коммерческого банка имеем:

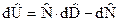(9.9)

т.е. получили автомодельную форму записи первого закона термодинамики коммерческого банка. Иными словами, уравнение (9.9) показывает, что все банки имеют один и тот же закон сохранения скорости прибыли в безразмерной форме, ВСЕ в этом смысле одинаковы. Но это и понятно, и ничего другого и быть не должно, так как ВСЕ банки делают одно и то же, одним и тем же механизмом: больше взять, меньше дать, быстро и долго.

Все детали, нюансы, особенности, отличия одного банка от другого сосредоточились в натуральных масштабах, в них же находятся параметры внешнего мира. Именно сами масштабы являются инструментами управления банком. Те параметры состояния банка, которые руководство может изменять по своей воле, следует изменять так, чтобы увеличивались масштабы N_# и D_#. Тогда увеличивается масштаб вожделенной скорости прибыли U_# ~ A*N_#*D_# .

С точки зрения теории обобщенного анализа результат (9.9) очень показателен: вместо 18 степеней свободы (13 - для самого банка и 5 - для внешней среды) получили всего 2 -е степени, 2 -а аргумента задач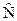и и 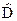. Теперь банком может управлять не только гений-банкир, а и хороший научный сотрудник в области точных наук. Выражение (9.9) представляет собой наивысшую степень обобщения и универсализации результата.

Для любопытных и любознательных продолжим применение метода термодинамического анализа к коммерческому банку, четко сознавая, что без натуральных масштабов это было бы очень затруднительно, если не невозможно.

В математике существует теория линейных дифференциальных форм вида

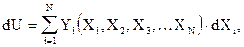
которые называются Пфаффовыми формами по имени известного немецкого математика. Пфафф доказал теорему о том, что двухчленная линейная дифференциальная форма всегда имеет интегрирующий множитель. Применим эту теорему к (9.9), обозначив этот интегрирующий множитель как . Тогда умножим (9.9) справа и слева на , получим

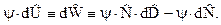(9.10)

Дифференциал 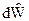уже является полным дифференциалом. Для (9.9) интегрирующий множитель удалось найти: 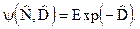Функция 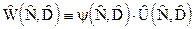теперь уже является функцией состояния, а не процесса, как . Ее изменение

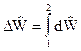
зависит уже только от координаты начала 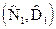и конца 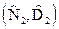движения фазовой точки банка, и НЕ зависит от траектории движения (см. рис 9.2.).

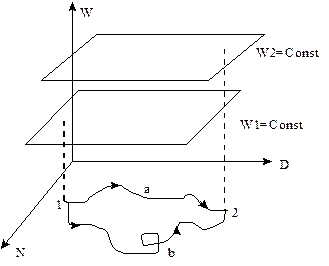
Рис 9.2. Иллюстрация смысла полноты дифференциала dW`.

DW` по траектории 1а2 равна DW` по траектории 1в2.

Получился очень важный результат для банковской практики: имеется принципиальная возможность определять стратегию развития коммерческого банка без архидорогого «русского авось», как это сейчас делают западные банки (отечественным, к сожалению, просто не надо).

Замечаниедля специалистов по термодинамике. Если выражение закона сохранения, которым оперирует термодинамика, не является полным дифференциалом, то сам термодинамический метод исследования далее просто останавливается. Дело в том, что апофеозом термодинамического метода анализа являются дифференциальные соотношения, которые не существуют в случае неполноты дифференциала. Сам способ записи закона сохранения в виде суммы элементарных количеств воздействия внешней среды на изучаемый объект

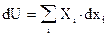
даже при известных уравнениях состояния X_i = X_i(x₁, x₂, x₃,....x_n) еще далеко не гарантирует полноту дифференциала dU.

Вообще, обращает на себя внимание тот распространенный факт, что термодинамика становится инструментом познания и расчетным аппаратом только для числа внешних воздействий равного двум. Если число внешних воздействий на рассматриваемую систему больше 2 -х, то термодинамический анализ системы почему-то отсутствует (в литературе не встречается).

Неявным решающим обстоятельством здесь, по-видимому, является именно теорема Пфаффа и именно для случая 2 -х родов взаимодействия. Но и в этом случае далеко не всегда проводится исследование полноты дифференциала, а сразу храбро пишутся дифференциальные соотношения, которые никому не нужны, так как неверны (и этому есть примеры даже в учебниках).

Хочется пожурить «чистых» математиков за то, что вот уже почти столетие физики не имеют условий получения полного дифференциала из Пфаффовой формы с числом слагаемых больше двух.

3. Дифференциальные соотношения термодинамики коммерческого банка.

Прежде всего договоримся об упрощении обозначений. Больше не будем писать крышечки сверху у безразмерных функций и аргументов, но помнить об их безразмерности будем. Выражение первого закона термодинамики (9.9) после приведения его к полному дифференциалу окончательно принимает вид:

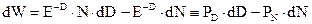(9.11)

Величины P_D и P_N по-прежнему будем называть потенциалами взаимодействия банка с внешней средой. Е = 2.73.

Среди всего разнообразия условий взаимодействия банка с внешней средой выделим очень важное подмножество: или P_N = const, или P_D = const, или N = const, или D = const. Это подмножество образует в термодинамике условия сопряжения банка с внешним миром. Это или условия сопряжения по потенциалам или по координатам. Эти условия сопряжения могут

1. или сознательно создаваться руководством банка, если оно понимает, чего хочет и как добиться поставленной цели,

2. или сознательно создаваться Центральным Банком России и федеральным правительством,

3. или случайно образоваться на какой-то период времени.

Во всех трех ситуациях руководство банка может приобрести инструмент понимания обстановки и руководства к действию во имя вожделенной прибыли. Таким инструментом и являются дифференциальные соотношения термодинамики (способ получения дифференциальных соотношений см. в лекции 2). Рассмотрим их и попробуем выяснить их физический смысл.

1. 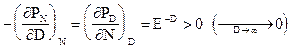(9.12)

Это диффсоотношение рассматривает условия сопряжения банка с внешней средой по координатам состояния и устанавливает равенство производных потенциалов по несопряженным им координатам.

Из (9.12) следует, что при N = const (банк насытился вкладами физических и юридических лиц, динамики роста / спада вкладов нет) увеличение объема кредитных денег D приводит к уменьшению потенциала вкладчиков P_N, вкладчики дружно начнут разбегаться и уходить к конкурентам. Такая ситуация реализовалась у тех Российских банков, которые получили на свои счета госбюджетные или региональные средства. Как только государство по каким-то причинам отнимет эти средства, наступит тяжелая ситуация: вкладчиков нет.

Если произошло событие D = const, то из (9.12) следует, что потенциал P_D коммерческого банка линейно зависит от объема вкладов N. Здесь банки вступят в ожесточенную борьбу друг с другом за вкладчиков, так как увеличение P_D означает рост доходов от кредитных операций.

Обращаем внимание руководителей банков, что е^-D ® 0 при D ® ¥ . Следовательно, для крупных банков потенциалы P_N и P_D становятся независимыми от несопряженных координат состояния. Корыстные интересы вкладчиков не вступают в противоречие с такими же интересами банка. У мелких и средних банков потенциал P_D сильно зависит от «капризов» вкладчиков, т.е. от N, следовательно, доходы банка очень неустойчивы, то густо, то пусто.

Сейчас величина N и, следовательно, D самая большая у сбербанка и Центробанка. Главное же заключается в том, что все 2500 коммерческих банков (по состоянию на 1998 год) России имеют суммарный капитал около $ 15*10⁶, а средний банк Японии или Западной Европы один имеет такой капитал. Следовательно, отечественные банки в среднем имеют капитал на три порядка меньше капитала банков развитых стран. Мизерность собственных капиталов у отечественных банков при всей их внешней помпезности и кураже делает их жизнь крайне неустойчивой. Вот они и то образуются на «миг», то исчезают. коммерческие В нищей стране банки ненадежны.

2. 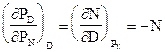т.к. из (9.11) (9.13)

Это диффсоотношение показывает, что при неизменном потоке заемщиков капитала (D = const) потенциал кредитования P_D = -N*P_N + const, т. е. увеличение объема вкладов N и увеличение потенциала P_N приводит к уменьшению потенциала кредитования и, следовательно, доходов банка. Этот вывод совершенно тривиален: при неизменном объеме кредита с ростом N приходится банку все больше платить по обязательствам перед вкладчиками.

Условие сопряжения P_N = const банка и вкладчиков приводит к тому, что координаты состояния N и D уже нельзя считать взаимно независимыми. В этих условиях руководство банка должно держать координаты состояния в соответствии с функцией:

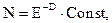или 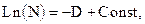(9.14)

причем величина const зависит от уровня стабилизации P_N = const.

Если руководство банка решит зафиксировать корыстный интерес вкладчиков, т.е. сделает P_N = const на какой-то период времени, то увеличение N сверх (9.14) приведет к росту обязательств банка перед вкладчиками и, как следствие, уменьшению прибыли банка. Если же вкладчики заберут свои депозиты, а «дружественные» банки не дадут рассматриваемому банку кредиты по каким-то причинам, т.е. N станет меньше (9.14), то у такого банка просто не будет достаточного количества актива D и прибыль снова упадет.

Эти выводы справедливы для мелких и средних коммерческих банков, т.е. большинства сегодняшних отечественных банков России. Для крупных банков, имеющих большой собственный капитал (D ® ¥, e^-D ® 0) фиксация P_N не играет большой роли, они могут обойтись на какое-то время и без вкладчиков.

3. 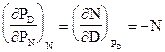т.к. из (9.11) 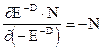(9.15)

Это диффсоотношение показывает, что при неизменном количестве вкладов физических и юридических лиц в сумме с кредитами «дружественных» банков потенциал кредитования

причем, эта const зависит от N. Следовательно, увеличивать корыстный интерес вкладчиков путем увеличения P_N не разумно, так как уменьшается P_D и, следовательно, доход и прибыль банка. Дело в том, что увеличиваются выплаты по обязательствам перед вкладчиками, поэтому прибыль уменьшается.

Если же государство как-то смогло фиксировать потенциал кредитования P_D , то координаты состояния теряют свою взаимную независимость:

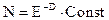или 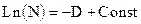(9.16)

но const зависит теперь уже от уровня фиксации P_D . Физический смысл этой взаимосвязи аналогичен (9.14).

4. 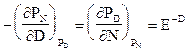т.е. из (9.11) (9.17)

Это диффсоотношение рассматривает условие сопряжения банка с внешней средой по потенциалам взаимодействия и устанавливает равенство производных потенциалов по несопряженным им координатам состояния.

Из (9.17) следует, что при фиксации государством величины P_D=const, увеличение объема кредитных, активных денег D уменьшает потенциал P_N , банк обнаружит уход вкладчиков и отказы в кредитах «дружественных» банков. Для крупных банков эта связь слабеет:

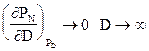
Если руководство банка пожелает фиксировать на каком-то уровне величину P_N , то с необходимостью проявится зависимость причем величина const зависит от P_N . Отсюда следует, что мероприятия по увеличению объема денег вкладчиков N приведут к уменьшению потенциала кредитования P_D, следовательно, прибыль банка уменьшится по двум причинам. Первая - уменьшится доход от операций с заемщиками капитала, вторая - увеличатся выплаты по обязательствам перед вкладчиками. В такой ситуации необходимо уменьшить величину N, т.е. прогнать вкладчиков, что опять-таки могут себе позволить лишь крупные банки.

Общее число дифференциальных соотношений для термодинамической системы с двумя видами взаимодействия с внешней средой равно ровно 4, других ограничений на решения руководителей банка нет.

Любой банкир, первый раз знакомящийся с такой для него экзотической наукой, как термодинамика, может спросить себя, а чего ради он должен следовать предписаниям диффсоотношений? Ответ предлагаем следующий.

1. Конечно, надо убедиться в адекватности предлагаемой термодинамической модели коммерческого банка, и это нормальная научно-исследовательская работа. При этом, может быть, придется модель уточнить, поправить, изменить уравнения состояния, но главное добиться качественного и количественного совпадения предсказаний теории и практических результатов, например, за предыдущий период времени работы банка. Во всяком случае, это уже дело техники, но не идеологии.

2. Законы природы, физики, представленные в виде императивов термодинамики, - объективны, действуют независимо от воли или безволия человека, который решил им не следовать. Это непослушание можно проанализировать и показать причину разорения. Служить Маммоне надо грамотно!

4. К вопросу рейтинга коммерческого банка.

Просматривая периодические журналы типа «Профиль» , «Коммерсант» , «Деловые люди», можно обнаружить аналитические статьи о состоянии банковского дела в России, можно увидеть многострочные и многостолбцовые таблицы, которые якобы позволяют сравнить деятельность банков между собой, решить какой из них «хороший», а какой «плохой». Поражает прежде всего явная эклектика, калейдоскопичность, изобилие параметров сравнения и, следовательно, определенная трудность анализа и синтеза выводов. Невольно вспоминаешь сакраментальное выражение времен развитого социализма: «Практика без теории - слепа, теория без практики - мертва!»

И действительно, изобилие параметров состояния в любой сфере деятельности является наиболее ярким и явным свидетельством отсутствия теории. Банковское дело далеко не единственный пример этого обстоятельства. В технике этим же недугом страдает надежность оборудования, надежность технологических систем. Только в ГОСТах по надежности фигурируют свыше 30 показателей надежности.

Если эту лекцию, посвященную термодинамике коммерческого банка, рассматривать как зародыш, эмбрион, предтечу теории банковского дела, то даже на этом уровне проблема определения рейтинга банков решается элементарно просто на основе натуральных масштабов. Теория обобщенного анализа доказывает, что интенсивность тех или иных процессов зависит не от каждого параметра порознь, а от некоторых их алгебраических комбинаций. В нашем случае такими комбинациями являются натуральные масштабы N_# и D_# координат состояния. Натуральный масштаб искомой функции U_# - скорости прибыли пропорционален произведению N_#*D_#. В связи с этим можно предложить следующий способ «оценки» деятельности какого-то банка. Необходимо рассчитать натуральные масштабы N_# и D_# каждого банка и найти отношения N / N_# и D / D_# , т.е. безразмерные координаты состояния банков. Чем ближе слева N / N_# к единице, тем успешнее конкурентная борьба этого банка за вкладчиков его региона, банк собрал все накопления своего региона и пускает их в кредитные операции. Чем больше N_#, тем больше забота банка об интересах вкладчиков, тем стабильнее его состояние, выше авторитет и имидж. Чем больше дробь D / D_#, тем больше скорость прибыли и, следовательно, больше годовая прибыль, выше дивиденты банка, больше средств для развития. Во всяком случае, комбинации параметров банка в виде N_# и D_# неизмеримо информативнее для аналитика, чем каждый из 18 параметров порознь.

5. Страшилка для банкиров.

Всем предпринимателям, бизнесменам и банкирам, естественно, хочется стабильности своего дела. Причем, стабильности в условиях динамичности, изменчивости во внешнем мире. Для мелких и средних банков эта изменчивость проявляется в хаотичности поведения вкладчиков: то толпой бегут в банк, то все дружно убегают. Кроме того, многие банкиры сами то завлекают вкладчиков, то прогоняют их, исходя из своих каких-то соображений. Короче говоря, вкладчики – морока для банкиров.

Выше было показано, что, чем крупнее банк, т.е. чем больше собственный капитал, тем больше величина D – работающих в кредите активов, тем меньше мороки с вкладчиками. Ростовщичество и есть стабильность. Следовательно, банки обречены укрупняться, сливаться во имя стабильности своего бытия.

Одновременно, со всей уверенностью можно утверждать, что появление на финансовом поле России иностранных банков с их огромными (по сравнению с Российскими) собственными капиталами означает крах отечественной банковской системы. Победитель в конкуренции предопределен. Придется отечественным микро – банкам скинутся на лоббирование в думе соответствующего закона.

6. Ссудный капитал и отечественная макроэкономика.

По определению К. Маркса, капиталом называются деньги, приносящие новые деньги. Сначала деньги были только средством обращения (бартер стал очень хлопотен), потом деньги стали средством накопления (золото и монеты из драгоценных металлов стали складывать в сундуки, вспомните «Скупого рыцаря» у А.С. Пушкина), наконец, деньги стали товаром (хочешь взять на время какую-то сумму – плати % от этой суммы).

Что означает взять кредит с % - ми для заемщика капитала? Это означает, что на какое-то время он может решать свои финансовые проблемы, связанные с недостатком оборотного капитала. А что означает кредит с % - ми для кредитора? Это означает, что через определенное время к нему вернется вся сумма кредита + % от этой суммы. Следовательно, не сеял, не пахал, но получил навар, который можно превратить в накопление (драгоценности, недвижимость, купить футбольный клуб «Челси» и т. д), т.е. изъять из сферы обращения деньги, происходит уменьшение оборотных капиталов. А что означают кредитные отношения в сфере обращения, т. е. для покупателей предметов потребления, услуг, жилья? Это означает рост цен не меньше, чем на величину % - та за кредит, а рост цен уменьшает покупательную способность населения страны. Здесь включается обратная положительная связь: с уменьшением покупательной способности населения происходит спад производства (ну, действительно, зачем производить что – то, если это не покупается?) Спад вызывает новый рост цен, и так до летального исхода. Только не забудем, что спусковым крючком является % за кредит.

Вывод: ссудный капиталь – раковая злокачественная опухоль в любой экономике. Ссудный капитал следует запретить на уровне конституции страны. Половина населения Земного шара спокойно живет без ссудного капитала, а в мусульманских странах ссудный капитал просто запрещен Кораном. Все крики о либерализации, о демократии, о цивилизованном обществе – это легитимизация ссудного капитала, его камуфляж, макияж на гнусной физиономии бандита.