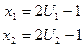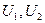Метод исключения
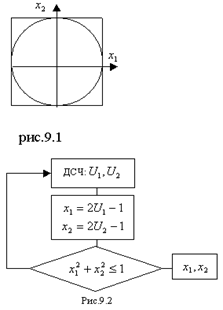
Сущность метода исключения поясним на примере. Пусть требуется получить координаты случайной точки в круге
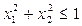
Можно организовать выбор случайной точки в квадрате, описанном около этого круга (рис.9.1)
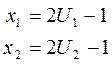
Значения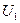 
и 
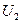берутся от ДСЧ. Для получения случайной точки в круге берут случайную точку в квадрате до тех пор, пока она не окажется внутри круга. Схема алгоритма изображена на рис.9.2.
|
|
|
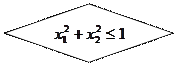
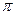/4 есть отношение площадей круга и квадрата. Поэтому среднее число повторений цикла вычислений для одной точки равно 4/ 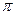= 1,3. Пусть теперь требуется имитировать случайную величину Х с плотностью f(х), относительно которой предположим: - f(х) сосредоточена на конечном отрезке [ а,в ], f(х) = 0, x 
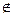[а,в]; - f(х) ограничена, f(х) 
,( 
).
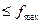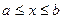График плотности распределения имеет вид (рис.9.3).Обозначим через G область а<х<в, 0<y<f(x).
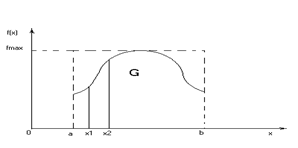
Рис. 9.3
Утверждение. Если точка (Х,У) равномерно распределена в области G, то ее первая координата Х распределена с плотностью f(х). Действительно, вероятность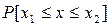 
равна площади заштрихованной фигуры, т.е.
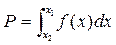
Таким образом, реализации случайной величины Х с плотностью f(х) можно получать, если X,Y координаты случайной точки в области G.
Случайную точку в области G получают методом исключения. Это приводит к следующим вычислениям.
1) От датчика случайных чисел получают два числа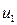 
и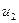 
.
2) Получаем координаты случайной точки в прямоугольнике
, 
, 
, 
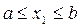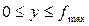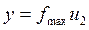
3) Проверяем условие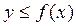 
. Если оно не выполняется, начинаем с пункта 1. При выполнении условия берем х в качестве значения Х.
Дата добавления: 2015-08-21; просмотров: 916;