Дисперсия света.

Дисперсией света называется зависимость показателя преломления 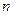вещества от частоты 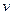или от длины волны 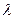. В результате дисперсии света происходит разложение белого света в спектр при прохождении его через призму. Впервые дисперсию наблюдал Ньютон.

Рассмотрим дисперсию света в призме (рис.1.).

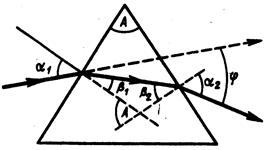Рис.1.

Монохроматический пучок света падает на призму с показателем преломления 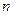под углом 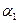. После двукратного преломления на левой и правой гранях призмы, луч отклоняется от первоначального направления на угол .

.

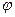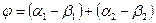По построению угол 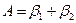и .

Рассмотрим случай, когда 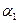и 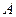малы, тогда малы и остальные углы 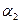, 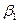и 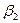. Значение синусов малых углов можно поменять на значения углов.

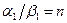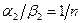, , но , отсюда .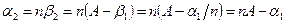

Подставим выражение для угла 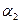в выражение для :

.

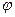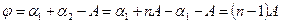Из этого выражения следует, что угол отклонения зависит от преломляющего угла призмы 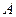и показателя преломления 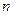. Если 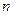зависит от длины волны ( 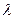), то лучи с разными длинами волн отклоняются на разные углы.

Из теории Максвелла следует, что 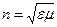, где 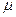- магнитная, а 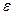- диэлектрическая проницаемость среды. Оптически прозрачные среды не намагничены, поэтому в оптической области спектра для всех веществ 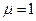и 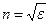. Экспериментальные данные противоречат теории Максвелла: 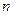- переменная величина, а 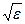- постоянная. Значение 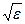также не согласуется с опытом. Эти противоречия устраняются электронной теорией Лоренца. Дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле.

Рассмотрим однородный диэлектрик, предположив, что дисперсия света является следствием зависимости 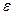от частоты 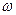световых волн. Диэлектрическая проницаемость вещества равна:

,

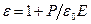где 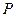- мгновенное значение поляризованности, 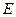- напряженность электрического поля. Тогда 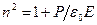. Из этого выражения видно, что 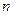зависит от 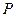. Основное значение в данном случае имеет электронная поляризация, то есть вынужденные колебания электронов под действием электрической составляющей поля волны. Для ориентационной поляризации молекул частота колебаний в световой волне очень высока ( 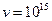Гц). Молекулы просто не успевают повернуться по полю.

В первом приближении можно считать, что вынужденные колебания совершают только внешние, наиболее слабо связанные ядром электроны – оптические электроны. Для простоты рассмотрим колебания только одного оптического электрона. Наведенный дипольный момент электрона, совершающего вынужденные колебания, равен 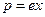, где 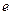- заряд электрона, 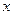- смещение электрона под действием электрического поля световой волны. Если концентрация атомов в диэлектрике равно 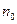, то мгновенное значение поляризованности равно: 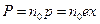. Подставив это значение в предыдущую формулу, получим: .

Задача сводиться к определению смещения 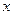электрона под действием электрического поля 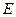. Поле световой волны является функцией частоты и меняется по гармоническому закону: 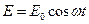. Уравнение вынужденных колебаний электрона для простейшего случая (без учета силы сопротивления, обуславливающей поглощения энергии падающей полны) записывается в виде:

,

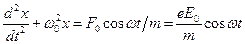где 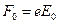- амплитудное значение силы, действующей на электрон со стороны поля волны, 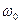- собственная частота колебаний электрона, 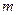- масса электрона. Решив это уравнение, найдем 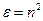в зависимости от констант электрона ( 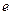, , 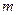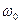) и частоты внешнего поля 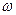, то есть решим задачу дисперсии.

Решение уравнения имеет вид 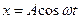, где 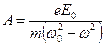. Подставляем это значение в выражение для 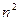, получим: 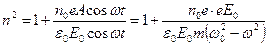. Итак квадрат показателя преломления равен:

.

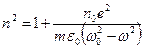Если в веществе имеются различные заряды 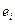, совершающие колебания с различными собственными частотами 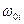, то

,

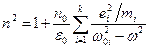где 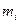- масса 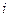-ого заряда.

Из последних выражений вытекает, что показатель преломления зависит от частоты внешнего поля, то есть полученные зависимости подтверждают явление дисперсии. На рис.2. приведен график зависимости 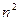от .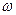

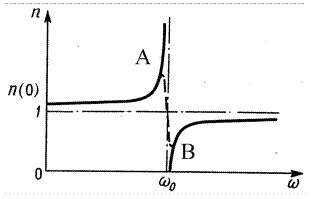Рис.2.

В области от 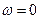до 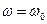, 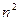больше единицы и возрастает с увеличением 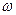(нормальная дисперсия). При 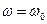, 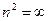. В области от 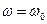до 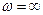, 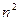меньше единицы и возрастает от 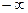до 1 (нормальная дисперсия). Стремление 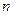вблизи собственной частоты 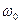к бесконечности получилась в результате допущения об отсутствии сил сопротивления при колебаниях электрона. Если учесть силы сопротивления, то график функции 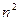от 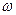вблизи точки 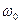задается штрихованной линией 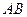. Область 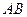- это область аномальной дисперсии ( 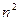убывает при возрастании ).

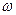При нормальной дисперсии 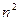возрастает с увеличением 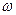(уменьшением 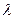). Зависимость показателя преломления от длины волны приведена на р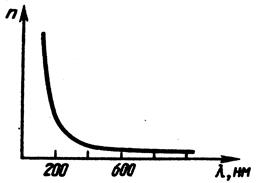ис. 3.

Рис.3

Это и приводит к появлению спектра (радуги).